管 土轴向动力相互作用等效弹簧系数取值

孙千伟，刘 威，李 杰

（同济大学土木工程学院，上海200092）

在对埋地管线进行地震反应分析时，如何反映管－土之间相互作用是一个关键问题.对于弹性地基梁模型，通常采用等效弹簧来反映管－土之间相互作用，这就使得弹簧系数的选取成为了问题的关键.一般情况下，管－土相互作用的等效弹簧系数可通过以下三个途径获得：解析法、有限元法和试验实测值［1］.由于有限元法建模的复杂性及试验实测数据的非普适性，因此很难广泛应用于工程实际.而对于解析法而言，虽然在表达式推导过程中引入了一些假设和对问题进行了一定的理想化处理，但其通常可以反映出问题的本源和关键，具有明确的物理意义，具有普适性.

至今，确定管－土相互作用等效弹簧系数的解析法主要有：Mindlin解法［2－3］、边界元法［4］及基于无限空间弹性体柱坐标系下的波动方程解法［1，5］等.20世纪70年代，Parmelee等［2］及Hindy等［3］利用半无限弹性空间的静力Mindlin解来获得在某一集中力作用下管周土体任意一点处的反应位移，从而确定管－土之间等效弹簧系数，但该方法得到的系数均为静力解.1987年，王海波等［4］采用边界单元法求解半无限空间中的管－土动力相互作用问题，给出了相应的等效弹簧系数，但该方法过于复杂.符圣聪［5］参考地下桩基中的薄层理论，从无限弹性空间圆柱坐标动力方程出发，推导了管－土动力相互作用的等效弹簧系数，但该系数是基于无限弹性空间条件推导的，未考虑场地表面对波动效应的影响.2000年，Matsubara等［1］从圆柱坐标系下的弹性波动方程出发，利用镜像的方式获得了半无限空间管－土轴向动力相互作用的等效弹簧系数的频域表达式，该表达式反映了等效弹簧系数更全面的信息，如其与频率、管道半径及埋深的关系等.但遗憾的是，文中并没有指出可以利用SH波的波动方程来反映管－土轴向动力相互作用，也没有对模型进行验证.

基于上述背景，本文首先从一维柱面SH波波动方程出发，重新阐释了文献［1］中推导的管－土轴向动力相互作用等效弹簧系数的解析表达式，并对主要影响参数进行分析；然后，从非一致激励作用下管－土动力相互作用振动台试验研究结果［6］出发，分析了小震（0.1g）作用下管－土接触面处剪切力与管－土相对滑移的关系，给出了试验条件下的管－土轴向动力相互作用等效弹簧系数，并将其与解析结果进行对比，进而验证了理论模型的合理性，并根据工程需要，给出了推荐值.

1 管-- 土轴向动力相互作用等效弹簧系数解析表达式

对于埋地管线而言，在均匀无限空间场地条件下，可将管周土体受到均匀谐和激励下的反应简化为弹性介质中的一维柱面波动问题.考察波动方程［7］，发现管－土轴向动力相互作用可以由SH波的波动作用来反映，如图1所示.

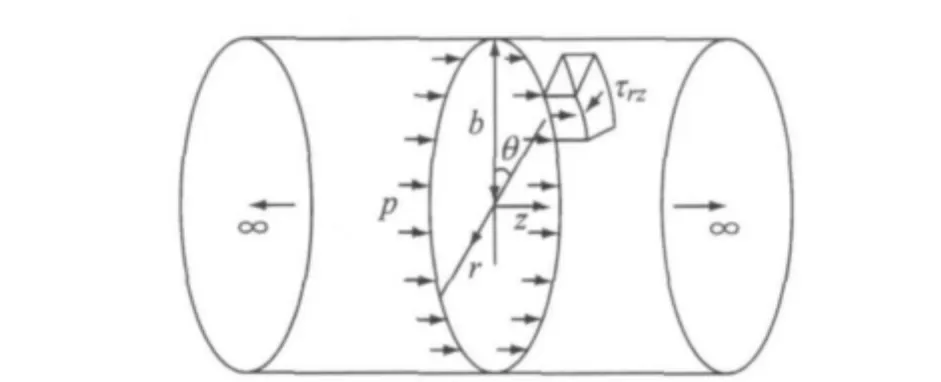
图1 一维柱面SH波波动问题Fig.1 One－dimensional SH wave motion theory in cylindrical coordinates

对应的动力平衡方程为

式中：r，z为柱面坐标系下径向及轴向坐标，τrz＝τzr为r—z平面内的剪应力，uz为柱面坐标下轴向位移，ρ为质量密度，t为时间.

应力—位移关系为

式中：G为管周土体剪切模量.

将式（2）代入式（1），得到柱面SH波的波动方程

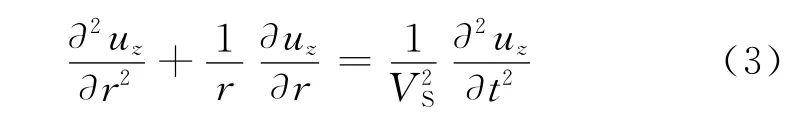
对式（3）进行Fourier变换，得到频域方程

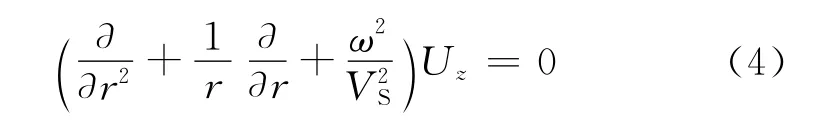
式中：Uz（r，ω）是uz（r，t）的频域位移，ω为圆频率.

根据文献［1］的研究思路，首先，对式（4）进行求解并引入接触面处应力平衡条件，来获得其在无限空间场地条件下的解答；然后，对埋地管线在无限空间场地获取镜像，进而得到半无限空间场地反应的频域解答；最后，根据管－土接触面处合力的平衡条件，得到管－土轴向动力相互作用的等效弹簧系数表达式［1］

式中：kA为轴向等效弹簧系数；δ（a0，γ）是a0和γ的函数，记为

式中：a0＝ωb／VS，为量纲一频率，b为管线半径；γ＝d／b；J0，J1为0，1阶Bessel函数；N0，N1为0，1阶Neumann函数；I1（a0，γ），I2（a0，γ）分别表示为

从上式可以看出，kA是G，a0和γ的函数，较全面地反映出了土体的动力特性.

2 影响参数分析

为了考察不同参数对弹簧系数取值的影响程度，对管线半径b、管线埋深d、剪切波速VS取不同值时δ的取值进行研究.

2.1 管线半径

假设d＝1m，VS＝100m·s－1，b分别取0.1，0.3，0.5，1.0m，δ—ω关系如图2所示.当ω＜41rad·s－1（f＜6.5Hz，f为频率）时，随着b增大，δ有增大的趋势，但增幅较缓，总体上处于0.5～1.0之间；当ω＝41rad·s－1（f＝6.5Hz）时，b大小对δ几乎没有影响，δ约等于1.1；当ω＞41rad·s－1（f＞6.5Hz）时，随着频率的增加，b对δ的影响逐渐加大，并呈现出随着b增大δ减小的趋势.这说明对于高频阶段，b大小对δ影响显著，是影响弹簧系数取值的主要原因之一，但在低频阶段影响不大.

图2 不同b值对应的δ—ω关系Fig.2 The relationship betweenδandωof different b

2.2 管线埋深

假设b＝0.3m，VS＝100m·s－1，d分别取0.5，1.0，2.0，5.0m及∞，δ—ω关系如图3所示.从图中可以看出，随着d加大，δ呈现出逐渐增大的趋势，并在一定频率范围内出现震荡现象，但当d增大到一定程度后（接近于∞时），δ渐渐趋于稳定.

图3 不同d值对应的δ—ω关系Fig.3 The relationship betweenδandωof different d

2.3 剪切波速

假设d＝1m，b＝0.3m，VS分别取50，75，100，150，200，500m·s－1，δ—ω关系如图4所示.从图中可以看出，VS取不同值时，δ在某一频率点上存在明显的变化.在该分界点前，δ基本稳定在1左右；在分界点后，δ随频率的增加出现明显的振荡现象，且有随VS增加而渐缓的趋势.当VS＝50，75，100m·s－1时，对应的分界点分别在ω＝57，83，110rad·s－1.这说明随着剪切波速的变化，影响δ取值的频率变化范围相应地发生变化.较小的剪切波速对应的频率影响范围较大；较大的剪切波速仅对较高频率阶段的δ有较大影响，对低频阶段几乎没有影响.

图4 不同VS值对应的δ—ω关系Fig.4 The relationship betweenδandωof different VS

从上面的分析可知，对于低频阶段，d对δ取值较为敏感，其他因素影响不明显；而对于高频阶段，上述的三种因素均对δ取值产生较大影响，不具有明显的规律性.为了统一表示这三种影响因素的影响程度，可用量纲一频率a0及管线埋深与管半径之比γ来反映，如图5所示［1］.

图5 不同γ取值下δ—a0的关系Fig.5 The relationship betweenδand a0of differentγ

图5给出了γ取不同值时，a0在0～1.0内的δ—a0关系.从图中可以看出，在a0取0～1.0时，δ限定在0.18～4.80范围之内，并且随着γ增大逐渐趋于稳定，当γ→∞时，δ值在1.0～3.0之间，对应的弹簧系数取值范围为1.0G～3.0G，其上限值3.0G即是通常采用的日本化工抗震设备准则的推荐值.

3 管 --土轴向动力相互作用等效弹簧系数试验值

为了验证管－土轴向动力相互作用等效弹簧系数取值的合理性，以埋地管线振动台试验结果为依据进行对比分析.2008年，孟海［6］对埋地管线进行了非一致激励作用下振动台模型试验，研究了埋地管线管－土动力相互作用.现从试验结果出发，给出试验条件下管－土轴向动力相互作用的等效弹簧系数.

3.1 试验概况

本试验为非一致激励作用下埋地管线振动台试验，如图6所示.试验首先设计了两个层状剪切箱A，B，将管线埋于其中，并在管体及其周围土体布置若干传感器，然后将剪切箱分别置于两个振动台上，通过对振动台沿管线轴向输入不同的激励，测试埋地管线及周围土体的反应.有关试验的详细情况参见文献［6］.图中AD6，AD8，BD6为测量管－土轴向相对位移的位移计，同时，在管道内外测点临近位置布置了应变片用以测量管体应变.

图6 埋地管线非一致激励振动台模型试验立面图（单位：mm）Fig.6 The evelation of shaking table test of buried pipeline under non－uniform excitation

3.2 试验结果分析

试验采用不同加速度峰值的输入激励对管－土动力相互作用进行了研究.从试验数据及现象看，当地震动加速度峰值较小时（0.1g），管－土之间的相对位移量很小，可以认为接触面处剪切力τ与相对位移u存在线性关系［6］.现提取输入加速度峰值为0.1g时的管－土相对位移（见图7）及管体应变ε（见图8）进行分析，研究管－土之间的动力相互作用，并给出其等效弹簧系数值.

假设两测点区域内管－土接触面处的剪切力分布均匀，并沿管周表面环向相等，管体应力亦沿管周表面环向相等，现取测点AD6与测点AD8之间的管段作为研究对象，如图9所示.该管段的平衡方程可表示为

式中：Δσ表示两测点间的管轴向应力之差；τ为管－土接触面处均匀分布剪切力；D为管道外径；A≈πDs，为管道横截面面积，其中s为管道壁厚；L为两测点间距离.

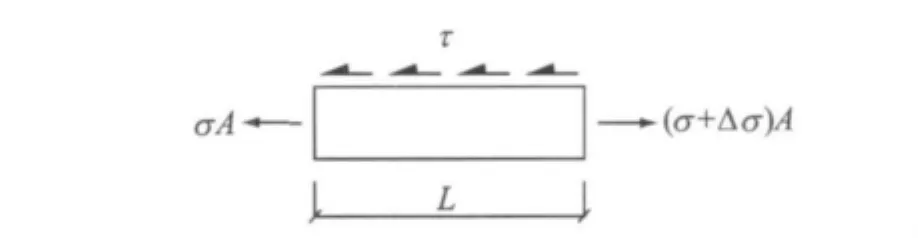
图9 两测点间管段受力图Fig.9 Force diagram of pipe segment between two measure points

将管道应力—应变关系代入式（9），可以建立管－土接触面剪切力与两测点应变差之间的关系为

式中：E为管材弹性模量，这里为钢管，其值为2.06×1011Pa；Δε为两测点间应变差.

取该管段管－土相对位移的平均值

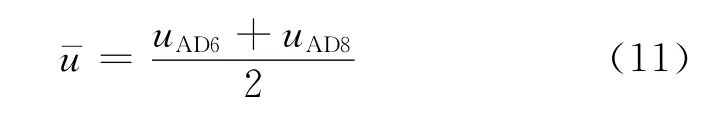
其中，uAD6，uAD8分别表示测点AD6和AD8的相对位移值.假设管－土相对位移沿管周表面相等，则管周土体受到的剪切合力与管－土相对位移在弹性阶段的关系可表示为

则管－土相互作用等效弹簧系数k可表示为

相应地，单位管段长度的弹簧系数为

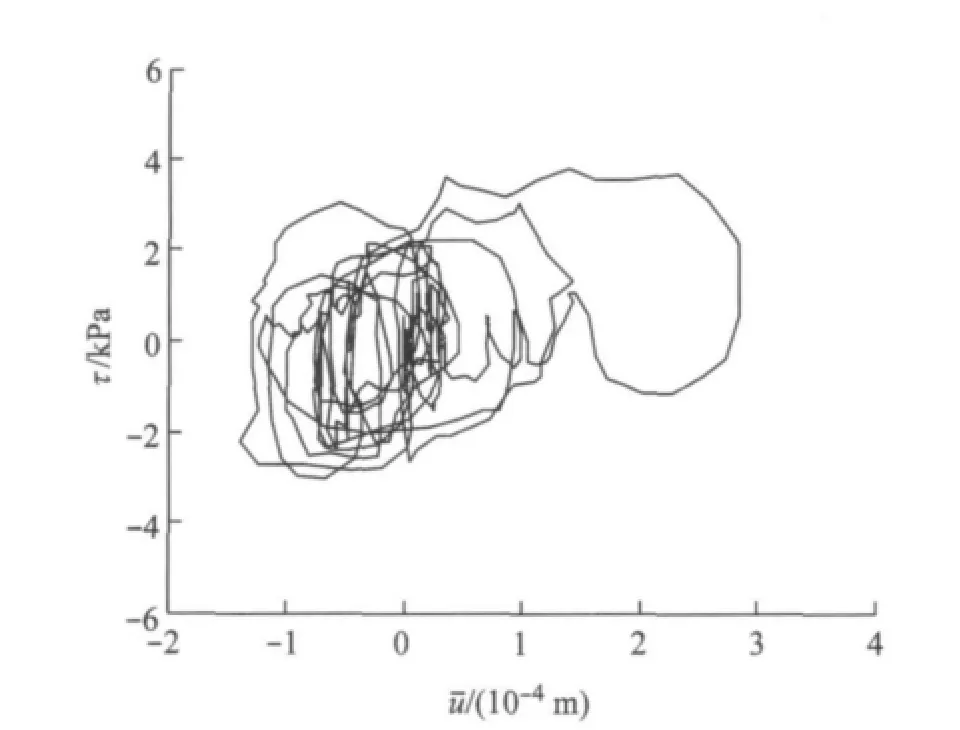
图10 管－土接触面处剪切力与相对位移平均值关系Fig.10 Relationship of shear stress and slippage on pipe－soil interaction surface

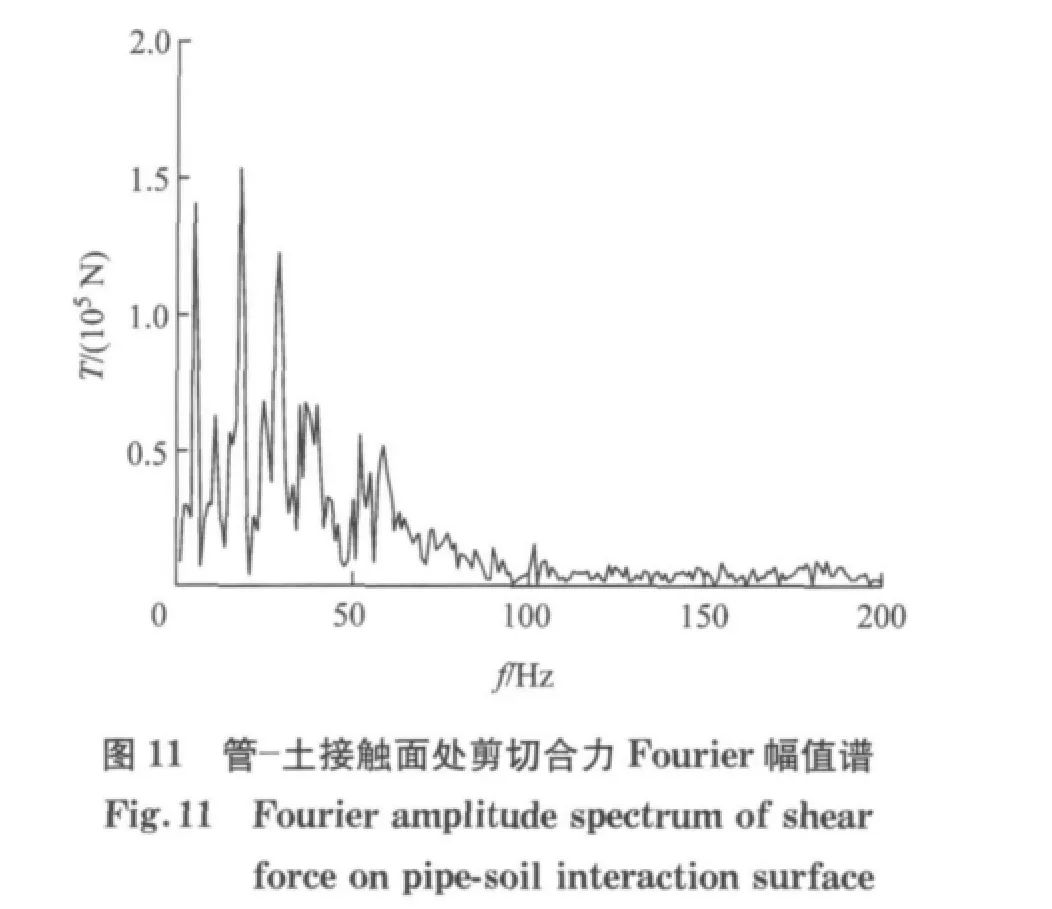
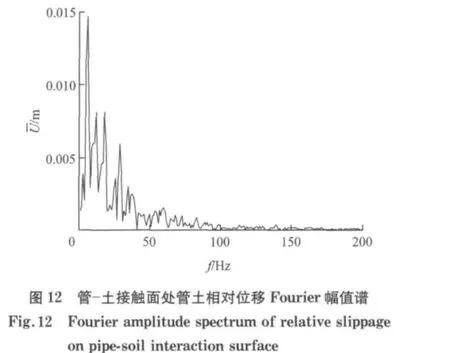
对上式中单位管段长度的剪切合力πDτ及相对位移平均值u进行Fourier变换，可以得到对应的幅值谱T（f）（见图11）及（f）（见图12）.

这样，可以得到管－土轴向动力相互作用等效弹簧系数的频域表达式

由上式可知，只要给定频率值即可计算出管－土轴向相互作用等效弹簧系数的频域值.

4 解析解与试验结果对比

对于解析解，由式（5）及式（6）可知，要计算等效弹簧系数，需要确定一些基本参数，这些参数包括：G，VS，土体卓越频率fp，b及d.

（1）G［6］模型试验采用的土体为粉质黏土，在试验前，利用动力三轴试验方法测定了土体动力参数.对于干密度ρd＝1.5g·cm－3、固结主应力比Kc＝1.2、围压σ3c＝50kPa的土体，测得其动剪切模量为Gdmax＝4.6MPa.

（2）VS［8］每次振动台试验前，都对模型土体进行了剪切波测试，测得剪切波速的平均值VS＝55～60m·s－1，这里取VS＝57.5m·s－1.

（3）fp

［8］根据试验资料，试验时首先利用低幅白噪声对模型土体进行扫描，激发其各阶振型，并由之计算出各阶频率，这里取一阶卓越频率fp＝6Hz.

（4）d和b 本模型试验采用的是钢管，2b＝219mm，d＝970mm.

通过上面的已知数据，可以计算量纲一频率a0＝2πfpb／VS＝0.072，γ＝8.86.将a0和γ代入式（6），可得δ＝1.23，对应的单位管线长度上的轴向等效弹簧系数kA＝δ（a0，γ）G＝5.66×106N·m－2.

对于振动台试验结果，将fp代入式（15），并结合图11，12所示Fourier幅值谱，可以计算等效弹簧系数kA＝5.27×106N·m－2.两者相对误差约为7.4%，说明在本试验条件下，两者结果吻合较好，验证了解析方法的合理性.

5 结论

本文利用解析法和振动台试验结果研究了管－土轴向动力相互作用等效弹簧系数取值问题，得到了等效弹簧系数的频域值.对于本试验条件，计算得到单位管段长度的轴向等效弹簧系数kA＝5.27× 106N·m－2，同等参数条件下采用解析法得到的弹簧系数kA＝5.66×106N·m－2，相对误差约为7.4%.虽然与真实值相比，无论是试验结果还是解析结果都不可避免地存在一定的偏差，但两者的吻合说明了解析表达式在一定程度上能够反映影响土弹簧系数取值的主要因素（如G，f，d，b，VS），从而验证了文献［1］给出的土弹簧系数解析表达式的合理性.对于工程实际情况，VS远大于b与f之积（a0＜0.1），从δ—a0关系图中可以看出这时δ限定在0.6～2.0之间，且随着γ增加逐渐增大，因此，若管－土之间未发生相对大位移，其轴向动力相互作用的等效弹簧系数可在0.6G～2.0G之间取值.

［1］ Matsubara K，Hoshiya M.Soil spring constants of buried pipelines for seismic design［J］.Journal of Engineering Mechanics，2000，126（1）：76.

［2］ Parmelee R，Ludtke C.Seismic soil－structure interaction of buried pipelines［C］／／Proceedings of the U.S.National Conference on Earthquake Engineering.Oakland：Earthquake Engineering Research Institute，1975：406－415.

［3］ Hindy A，Novak M.Earthquake response of underground pipelines［J］.Earthquake Engineering ＆Structural Dynamics，1979，7（5）：451.

［4］ 王海波，林皋.半无限弹性介质中管线地震反应分析［J］.土木工程学报，1988，20（3）：80.

WANG Haibo，LIN Gao.Seismic response of the pipeline buried in three dimensional semi－infinite elastic medium［J］.China Civil Engineering Journal，1988，20（3）：80.

［5］ 符圣聪.用于埋管抗震计算的地面位移和地基反力系数［J］.特种结构，1992（4）：4.

FU Shengcong.Ground displacement and coefficient of subgrade reaction for buried pipeline seismic evaluation［J］.Special Structure，1992（4）：4.

［6］ 孟海.埋地管线－土动力相互作用非一致激励振动台试验模型研究［D］.上海：同济大学土木工程学院，2008.

MENG Hai.Shaking table tests of soil－pipe dynamic interaction under non－uniform earthquake wave excitation［D］.Shanghai：College of Civil Engineering of Tongji University，2008.

［7］ 杜修力.工程场地波动理论与方法［M］.北京：科学出版社，2008：282.

DU Xiuli.Theories and methods of wave motion for engineering［M］.Beijing：Science Press，2008：282.

［8］ 王琴.地下管线非一致激励地震反应分析［D］.上海：同济大学土木工程学院，2008.

WANG Qin.Seismic response analysis of underground pipelines under non－uniform earthquake wave excitation［D］.Shanghai：College of Civil Engineering of Tongji University，2008.