复杂载荷作用下潜艇结构疲劳裂纹扩展预报方法

张鼎，黄小平

（上海交通大学海洋工程国家重点实验室，上海 200240）

1 概述

潜艇由于必须不定期的上浮和下潜，承受着反复作用的外压随机载荷，面临着疲劳问题。目前采用的疲劳寿命预测方法大致可分为2类:一类是基于SN曲线和Palgren-Miner线性累积损伤的疲劳理论（Cumulative Fatigue Damage，CFD）;另一类是基于疲劳裂纹扩展率曲线的疲劳裂纹扩展理论（Fatigue Crack Propagation，FCP）。由于海洋结构物几何形状及所受载荷的复杂性，CFD理论预测疲劳寿命的结果不甚理想。研究表明，FCP理论能克服CFD理论的缺陷［1］。一种预测疲劳裂纹扩展率的好方法是正确预报疲劳寿命的关键，尽管关于裂纹扩展率模型有不少研究报道，但是很少有模型能模拟在实验中出现的各种特殊现象［2］。

自Paris等［3］在线弹性断裂力学基础上给出第1个应力强度因子幅和裂纹扩展速率的关系表达式以来，关于裂纹扩展率的不同表达式已不下几百个。到目前为止，所有这些关系式都是经验或半经验的。为了减少由于所取经验参数的不同带来的随意性，不少学者在裂纹扩展率统一公式方面做出了不懈的努力。McEvily等［4］发表了一系列属于部分闭合的裂纹扩展率模型，此模型不仅可以模拟初始缺陷及载荷次序的影响，还可以模拟在实验中出现的其他各种特殊现象。但是此模型只适合线性区域或极限水平附近区域，且只对理想弹塑性材料有效。在McEvily模型基础上，崔维成、黄小平等［5］提出了统一疲劳裂纹扩展模型，此模型在以下几个方面做了改进:

1）引入了不稳定断裂情况;

2）用虚拟强度来代替材料的屈服强度;

3）引入过载/低载参数来模拟循环载荷进程中的过载迟滞和低载加速现象。

最近，王芳等［6－8］在前面研究的基础上又做了如下改进:

1）将断裂韧性当成一个关于裂纹长度的变量;

2）将裂纹张开水平处的应力强度因子表示为裂纹长度的函数，进一步完善了统一疲劳裂纹扩展模型。模型将疲劳裂纹扩展的3个扩展区域统一起来，并能解释更多的疲劳试验现象［8］。

本文主要进行了以下3个方面的工作:

1）介绍了统一疲劳裂纹扩展模型的基本表达式;

2）将此模型和焊趾表面裂纹应力强度因子的计算方法以及焊接残余应力引起的应力强度因子的计算方法结合起来，给出了一种复杂载荷作用下潜艇结构疲劳裂纹扩展预报方法;

3）将服从Weibull分布的随机载荷系列编排为升序、降序载荷谱及随机载荷谱，预报了潜艇锥柱结合壳焊缝焊趾处表面裂纹在这3种载荷谱下的疲劳裂纹扩展情况，并分析了随机载荷谱下载荷次序效应及初始裂纹尺寸对疲劳裂纹扩展行为的影响。

2 统一疲劳裂纹扩展模型

文献［8］运用统一疲劳裂纹扩展模型对不同载荷比下各种材料的疲劳裂纹扩展率进行了预报，并将预报结果与实验结果进行了对比，对比结果证明了该模型的准确性。其中，模型的基本表达式为［7－8］:

式中:A为材料及环境常数，（MPa）－2;R为应力比，定义为Smin/Smax;ΔKeffth为门槛值处的有效应力强度因子为当应力比R=0时的应力强度因子幅门槛值为材料的平面应变断裂韧性为裂纹开口状态函数，定义为Kop/ΔK;KC为材料的断裂韧性为过载时的最大应力强度因子为低载－过载引起的应力强度因子幅为裂纹尖端塑性区大小，m;rOL为过载时裂纹尖端塑性区大小，m;rUL为低载时裂纹尖端塑性区大小，m;Φ为载荷次序修正因子;Y为裂纹实际长度的几何因子;σV为材料的虚拟强度，MPa;re为量级在1 μm左右的材料内部缺陷长度;λ为塑性区大小系数;γ为载荷效应指数;A0，A1，A2和A3为裂纹张开函数的系数;σf1为流变应力，MPa;α'为平面应力/应变约束参数;α为计算材料虚拟强度的参数;w为裂纹平板试件的宽度，m;t为裂纹平板试件的厚度，m;Kmax，fop和KC均为裂纹长度的函数。

3 潜艇结构表面裂纹应力强度因子计算

3.1 压弯组合应力下焊趾表面裂纹应力强度因子计算

由于潜艇结构的特点以及所受载荷的特殊性，其锥柱结合壳焊缝处受到压弯组合应力作用。焊接结构在压弯组合应力下焊趾表面裂纹应力强度因子的一般形式为［9］:

其中:σb为弯曲应力;a为裂纹深度;c为裂纹半长; w为板宽;MK为压弯组合应力下焊接结构应力强度因子修正系数;KR为残余应力引起的应力强度因子。适用范围:0＜a/c≤1.0，0＜a/t≤1.0，2 c/w≤0.5，0≤φ≤π。

3.2 焊趾处应力集中的影响

当缺陷或裂纹位于局部应力集中区时，在计算K时必须考虑应力集中场的影响，对于焊趾表面裂纹来说，应力强度因子放大系数MK是裂纹尺寸，接头的几何参数以及载荷的函数。对于很浅的表面裂纹，可以认为MK=Kt。当裂纹深度增加时，裂纹尖端就逐渐远离应力集中区域，MK随裂纹深度的增加而减小，在厚度为t的平板上的焊接接头。对于对接焊缝，当a/t=0.1时，MK可认为减小到1.0［10］，对于突出成圆弧形的双面加强高对接接头，其简图如图1所示，在MK＞1.0的范围内，文献［11］给出了一种对接接头的MK计算方法:

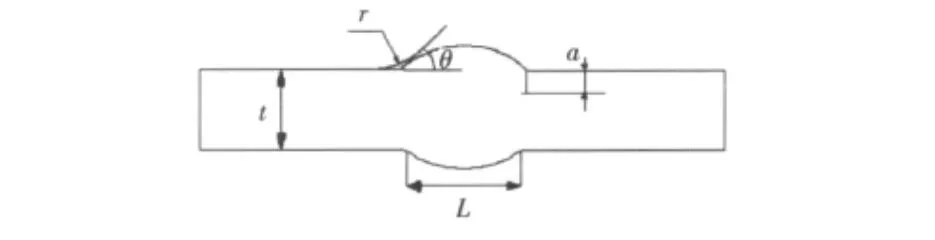
图1 对接接头简图Fig.1Sketch of weld joint

3.3 焊接残余应力引起的应力强度因子计算

在焊接结构加工过程中，由于焊接热循环的作用，引起接头局部不均匀的热塑性变形和相变，产生了自相平衡的残余应力。一般而言，大型的压力容器焊接成形后，难于进行整体的退火处理，在容器壳体的曲率突变处，往往存在着残余应力。对于平行于焊缝的焊趾表面裂纹，应当考虑垂直裂纹面的焊接残余应力的影响。文献［12］建议垂直焊缝方向的焊接残余应力在焊趾处表面的取值为:

式中:σR为残余应力;σY为材料的屈服强度。

当保守计算时，可认为残余应力沿壁厚均布且等于表面处的残余应力。对于残余应力引起的应力强度因子的计算，借用Newman-Raju公式［13］的拉应力部分，将残余应力简单的视为拉应力即可，故残余应力的应力强度因子计算式可如下表示:

4 实例分析

4.1 潜艇载荷谱分析

潜艇结构的疲劳热点部位是锥柱结合壳连接焊趾处，焊趾表面裂纹及其疲劳扩展导致结构的失效是该结构破坏的主要形式［14］。文献［15］从疲劳损伤的角度出发，考虑可能出现的最危险情况下的载荷统计特性，探讨了建立潜艇所受外压载荷模型的方法。在此基础上，给出了典型的潜艇或潜水器外压载荷分布概率密度函数。本文假设潜艇的极限深度为450 m，且下潜深度符合Weibull分布，其概率密度函数和分布函数如下所示［15］:

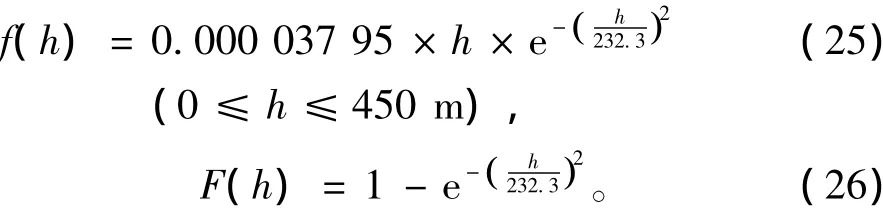
由于下潜深度是随机的，若直接由数学软件工具Matlab生成服从式（25）的随机数时，随着数据的增多，必然会产生大于450 m的数据。为了尽可能使产生的随机数可靠，首先利用Matlab随机产生40 000个从0～0.975的服从均匀分布的随机数，其中，0.975为极限深度450 m对应的累积概率，由式（25）得到。然后将这些数据转化为服从Weibull分布的数据。

为了使计算过程简单，认为潜艇在每次下潜到一定深度后都潜出水面。当潜艇到达水面时，将只承受残余应力;潜艇在水下时承受弯曲应力、压缩应力和残余应力的影响。弯曲应力和压缩应力随深度变化，残余应力作为常量来考虑。且残余应力为交变载荷的最小应力，它通过应力比R影响裂纹的扩展速率。图2为载荷随机数据分布图，由于数量较多，只列举了前200个载荷随机数。其中，弯曲应力σb与压缩应力σc可通过下式来计算［16］:

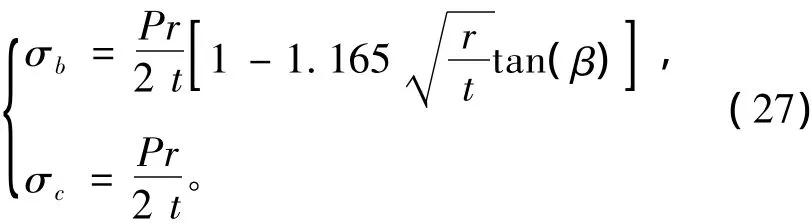
式中:P为海水外压，取1 MPa，即对应100 m水深;r为圆柱壳内径;β为锥柱结合角。

图2 服从Weibull分布的载荷随机数据分布Fig.2Random loading obey the Weibull distribution

本文将生成的随机载荷系列编排为升序、降序载荷谱及随机载荷谱，在此基础上分析了潜艇结构在这3种载荷谱下的疲劳裂纹扩展情况。同时探讨了在随机载荷谱下，载荷次序效应及初始裂纹尺寸对潜艇结构疲劳寿命的影响。图3和图4分别为升序载荷谱和降序载荷谱的示意图。其中，结构材料为921钢，其屈服强度600 MPa，计算过程中，模型选取的系数为:A=1.39×10－10，m=2.325，n=6，γ=4.8。

4.2 预报结果分析

对于初始状态的裂纹，由一般工业上无损探伤可以检测到的裂纹的大小或允许最大的缺陷尺寸的大者作为初始裂纹的尺寸:a＞0.05 mm，c＞0.5 mm。如图5所示，完成相同的循环次数后，当初始裂纹深度a为0.2 mm，初始裂纹长度c分别取5 mm和7 mm时，均可得到升序载荷谱下最终裂纹深度值最大，随机载荷谱时次之，降序载荷谱时最小。在降序载荷谱下，载荷从大到小，开始阶段载荷较大，裂纹扩展速度较快，但随着载荷逐渐减小，裂纹扩展速度越来越慢;另一方面，在升序载荷谱下，载荷从小到大，开始阶段载荷较小，裂纹扩展速率较小，当循环到一定次数后，随着载荷越来越大，裂纹扩展速率越来越大。

图3 升序载荷谱块Fig．3Ascending loading spectrum

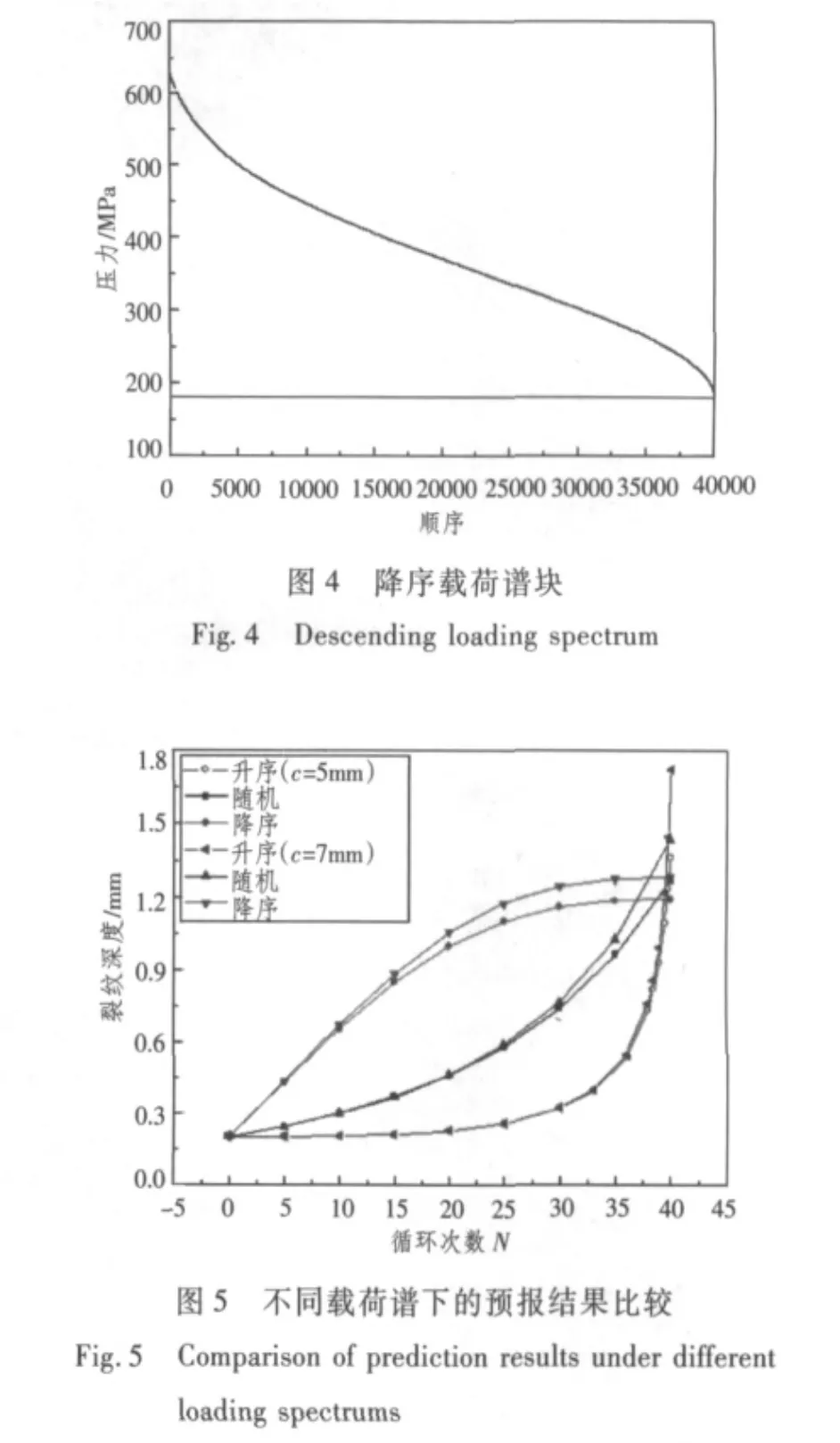
表1表示载荷循环（40000次）完成后，不考虑载荷次序效应时不同的初始裂纹尺寸组合所对应的最终裂纹深度。表2为考虑载荷次序效应时的最终裂纹深度情况;表3为比较表1和表2数据，考虑载荷次序效应后最终裂纹深度的减幅。从表1和表2可以看到，当初始裂纹深度a和初始裂纹长度c的取值均较大时，最终裂纹深度值亦较大。原因为:当初始裂纹尺寸较大时，由上文裂纹扩展率公式可知，裂纹长度和深度方向的扩展速率均较大，故当循环次数相同时，初始裂纹尺寸越大，最终裂纹深度值越大。初始裂纹的尺寸大小对裂纹扩展影响显著，可见合理的确定初始裂纹尺寸是分析裂纹扩展非常关键的一步。

表1 随机载荷谱下不考虑载荷次序效应时的最终裂纹深度Tab．1Estimate of final crack depth after 40000 cycles under random loading spectrum without considering the loading sequence interaction

表2 随机载荷谱下考虑载荷次序效应时的最终裂纹深度Tab．2Estimate of final crack depth after 40000 cycles under random loading spectrum considering the loading sequence interaction

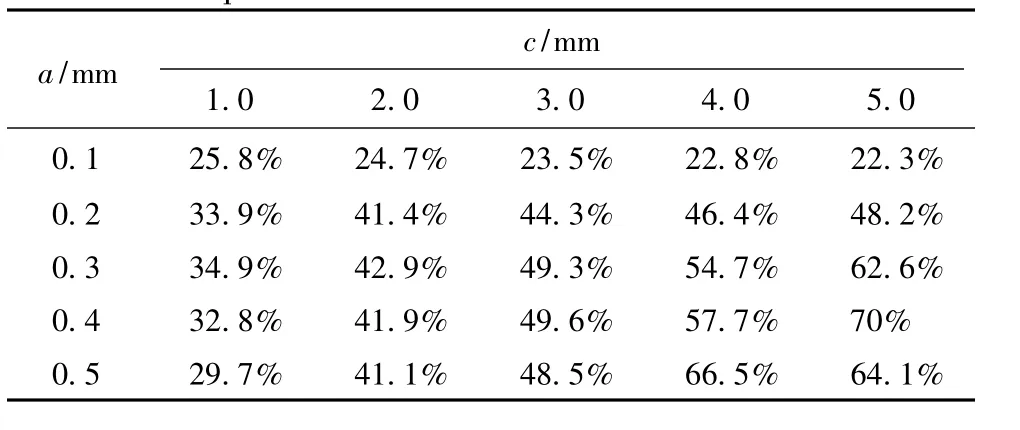
表3 随机载荷谱下考虑载荷次序效应后裂纹深度的减幅Tab．3Decreasing amplitude of crack depth under random loading spectrum after considering the loading sequence interaction

从表3还可看到，对于服从Weibull分布的载荷谱，考虑载荷次序效应后大部分裂纹深度的减幅都高达30%以上，甚至高达70%，过载迟滞现象很明显，说明载荷次序效应的影响很大。原因是Weibull分布的载荷谱较宽，出现载荷大幅度跳跃的可能性较大，而载荷次序的修正因子跟载荷变化范围有关，即如果高载后的载荷越小，由上文裂纹扩展率公式可知，载荷次序的修正因子Φ越大，裂纹扩展速率越小。

5 结语

本文介绍了统一疲劳裂纹扩展模型的基本表达式，同时将此模型与焊趾表面裂纹应力强度因子计算方法以及残余应力引起的应力强度因子的计算方法结合起来，预报了潜艇锥柱结合壳焊缝焊趾处表面裂纹在几种典型载荷谱下的疲劳扩展行为，得到结论:

1）疲劳裂纹扩展预报方法中考虑了载荷次序效应，应力比，门槛值，焊趾放大系数和残余应力等因素的影响，结合相应的载荷谱，能有效预报潜艇结构在复杂载荷作用下的疲劳裂纹扩展行为。

2）将满足Weibull分布的随机载荷系列编排成升序、降序载荷谱及随机载荷谱。通过对这些载荷谱进行预报分析可以看到，完成相同的载荷循环次数后，在升序载荷谱下潜艇结构表面裂纹的最终裂纹深度值最大，随机载荷谱时次之，降序载荷谱时对应的最终裂纹深度值最小。

3）潜艇结构的疲劳裂纹扩展预报结果表明，在随机载荷谱下，载荷次序效应对结构疲劳寿命的影响很明显。

4）潜艇结构疲劳裂纹扩展寿命分析中确定合理的初始裂纹尺寸非常重要。

5）统一疲劳裂纹扩展模型的参数相对较多，对于基础数据不充分的结构强度评估有较大难度，在推向实际运用之前还需做更多的实验验证工作。

［1］CUI W C．A feasible study of fatigue life prediction for marine structures based on crack propagation analysis［J］．Journal of Marine Environmental Engineering，2003，217 （5）:11－23．

［2］FRICKE W，CUI W C，LEE H L，et al．Comparative fatigue strength assessment of a structural detail in a containership using various approaches of classification societies［J］．Marine Structure，2002，15（1）:1－13．

［3］PARIS P C，GOMEZ M P，ANDERSON W E．A rational analytical theory of fatigue［J］．The Trend in Engineering，1961，（13）:9－14．

［4］McEVILY A J，BAOH，ISHIHARAS．Amodified constitutive relation for fatigue crack growth［M］．Beijing: Higher Education Press，1999．329－336．

［5］CUI W C，HUANG X P．A general constitutive relation for fatigue crack growth analysis of metal structures［J］．Acta Metall Sinica，2003，（16）:342－354．

［6］WANG Fang，CUI Wei-cheng．On the engineering approach to estimating the paremeters in an improved crack growth rate model for fatigue life prediction［J］．Ships and Offshore Structure，2010，（5）:227－241．

［7］CUI Wei-cheng，WANG Fang，HUANG Xiao-ping．Towards a unified fatigue life prediction（UFLP）method for marine structures:an overview［A］．Proceedings of the ASME 2010 29th International Conference on Ocean，Offshore and Arctic Engineering［C］．Shanghai，2010．981－989．

［8］CHEN Feng-luo，WANGFang，CUIWei-cheng．Applicability of the improved crack growth rate model for a wide range of alloys under constant amplitude load［J］．Journal of Ship Mechanics，2010，14（12）:1349－1360．

［9］黄小平，石德新．压弯应力下焊趾表面裂纹疲劳性能试验研究［J］．船舶力学，2002，2（1）:37－43．

HUANG Xiao-ping，SHI De-xing．Experiment on fatigue behaviour of surface cracks at weld toe under combination stresses of compressing and bending［J］．Journal of Ship Mechanics，2002，2（1）:37－43．

［10］BS7910-1999，Guideonmethodsforassessingthe acceptability of flaws in structures［S］．

［11］张毅，黄小平，崔维成，等．对接接头焊趾应力集中有限元分析［J］．船舶力学，2004，8（5）:91－99．

ZHANG Yi，HUANG Xiao-ping，CUI Weic-heng，et al．Finite element analysis on stress concentration at weld toe of butt-welded joints［J］．Journal of Ship Mechanics，2004，8（5）:91－99．

［12］黄小平，贾贵磊，崔维成，等．海洋钢结构疲劳裂纹扩展预报单一扩展率曲线模型［J］．船舶力学，2011，15（1－2）:118－125．

HUANG Xiao-ping，JIA Gui-lei，CUI Wei-cheng，et al．Unique crack growth rate curve model for fatigue life prediction of marine steel structures［J］．Journal of Ship Mechanics，2011，15（1－2）:118－125．

［13］NEWMAN J C，RAJU I S．Analysis of surface cracks in a finite plate under tension or bending loads［R］．NASA TP－1579，1979．

［14］黄小平，崔维成，石德新．潜艇锥柱结合壳焊趾表面裂纹疲劳寿命计算［J］．船舶力学，2002，6（4）:62－68．

HUANGXiao-ping，CUIWei-cheng，SHIDe-xing．Calculation of fatigue life of surface cracks at weld toe of submarine cone-cylindershell［J］．JournalofShip Mechanics，2002，6（4）:62－68．

［15］黄小平，崔维成．潜艇疲劳载荷的概率模型［J］．海洋工程，2003，21（3）:18－23．

HUANG Xiao-ping，CUI Wei-cheng．Probability model of fatigue loading for submarines and submersibles［J］．The Ocean Engineering，2003，21（3）:18－23．

［16］戴自昶．锥－环－柱结合壳和锥－柱结合壳应力的近似解［J］．舰船科学技术，2002，24（5）:1－8．

DAI Zi-chang．Approximate solutions of stress in conetoroid－cylinder and cone-cylinder complex shells［J］．Ship Science and Technology，2002，24（5）:1－8．