一种改进的混响精细结构模型及其特性分析

吕维，王志杰，李建辰，王明洲，胡桥，杨宝民

（1．中国船舶重工集团公司第七○五研究所，陕西西安710075; 2．水下信息与控制重点实验室，陕西西安 710075）

0 引言

与雷达杂波相似，鱼雷混响也具有空时耦合特性。当声呐平台有一定的运动速度时，不同方向的混响具有不同的多普勒频移，这使得混响谱在较大的范围内扩展，目标回波被掩盖在扩展的混响中，给目标的探测增加了难度。混响谱的这种空时二维耦合特性，使得利用雷达空时自适应方法对混响进行抑制成为一种可能。但与雷达环境不同，鱼雷水下环境的声速远比电磁波传播速度低，散射点的运动对混响回波波形的影响往往不能忽略，即回波信号不仅在时宽和幅度受到压缩和扩展，还产生了频率的调制和扩展，所以雷达杂波的窄带模型在水下混响回波建模中并不适用。以往研究混响空时特性的文献中［1－3］，建立的混响模型都是基于简化的窄带模型上，忽略了回波时域扩展和频率调制，并不能真实反映混响的空时特性。本文从水下声信号的特点出发，利用单元散射原理，对界面混响进行精细结构建模、仿真，并分析了界面混响的空－时－频统计特性。

1 散射点回波原理

混响模型的仿真主要分为单元散射模型和点散射模型2种。单元散射模型是假设散射体均匀分布在整个海洋，因此可以把海洋分成许多单元，每个单元中都含有大量的散射体。这种方法在声呐仿真中的应用最为普遍。单元散射模型主要有基于散射元功率谱模型［4－5］和基于散射元时间信号叠加模型2种［1－6］。本文利用散射元时间信号叠加模型进行混响仿真，其应用的理论基础是散射点回波原理［2］。其原理为:对于运动声呐平台而言，第m个散射点对第n个阵元的回波模型［7］，如图1所示。

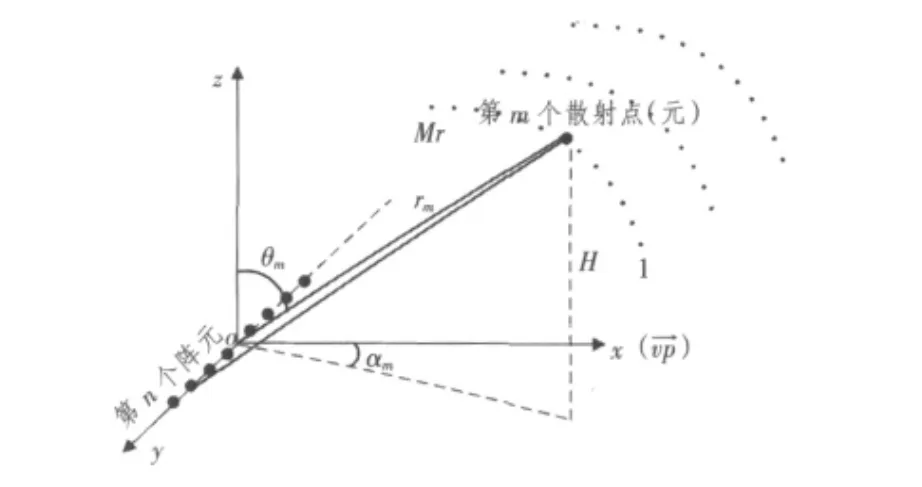
图1 散射元分布图Fig.1Distribution of scatter location

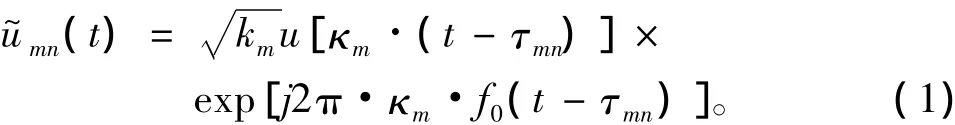
其中，时间尺度κm=1+βm=（c+v0m）/（c－v0m），反映了散射点与运动平台间相对运动时产生的波形压缩和扩展;υ0m为第m个散射点与运动平台间的相对径向运动速度，在散射点与运动平台接近时为“+”，反之为“－”;τmn=（2·rm/c－dn·sinθm·sinαm/c），其中dn·sinθm·sinαm/c为第m个散射点与第n个阵元相对于阵元中心的声程差，dn为第n个阵元距阵元中心的距离。在雷达电磁环境下，电磁波传播速度c=3*108m/s＞＞υ0，所以κ=1+β≈1，β≈2v0/c，fm=βf0，τmn=2rm/c。由此散射点回波模型可以简化为:

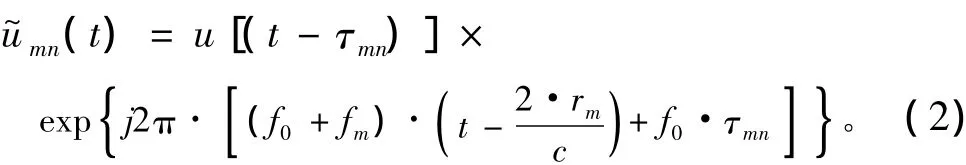
雷达空时自适应的杂波模型是建立在这一简化模型基础上的，目前研究的空时自适应理论在声呐中应用的相关文章［1－5］也都采用以上的简化模型。与雷达电磁环境不同，鱼雷主动声呐所处的水下环境更为复杂，尤其是水下声速不再满足c=1500 m/s＞＞υ0，因此，建立混响模型的时候要考虑到声速的影响。本文采用式（1），即经典的散射点宽带回波模型，引入了时间尺度κ，既考虑了时间包络的伸缩（即时宽和幅度受到压缩或扩展），又考虑到了混响对原始信号的频移以及频率调制，从而更准确地反映了水下回波的特点，并利用此模型建立混响单元散射回波模型。

2 精确混响模型

为简化计算，对混响作如下假设:

1）传播路径全为直线，除了球面扩展衰减之外，其他衰减一概不计;

2）在任意给定时刻，散射体都均匀分布在整个产生混响的面积和体积中，散射元不作方向固定的运动，只是在原位置作方向随机的运动;

3）散射体密度足够大，保证在体元或面元中有足够的散射体;

4）脉冲宽度足够短，它在体元或面元尺度方位的传播效应可以不计;

5）不存在多次散射（也不计混响产生的混响）。

考虑图1的情形，声呐平台以速度vp沿着X轴运动。第m个散射元的方位角和俯仰角分别为θm［θm=cos－1（H/rm）］和αm，到阵元中心的距离为rm。设声呐的发射信号的频率为f0，利用经典散射点回波模型，可以得到第n个阵元的回波模型如下:

其中，‘·*’为矩阵对应元素相;e～m为第n个阵元的幅度和相位误差;PMr［Mr，1］为第1～Mr个散射元的回波平均幅度，与发射信号强度、散射元散射强度及其所代表的面积或体积、发射和接收的波束指向性、传播扩展衰减、海水吸收等因素有关;AMr［Mr，1］为第1～Mr个散射元随机的幅度及相位调制信号，它的起伏大小决定了该散射元的多普勒扩展的程度［1－2］;U～Mr［Mr，1］为第1～Mr个散射元的回波，计算参见式（1）。

在计算界面各散射元空间位置时，考虑到声呐的空间角度分辨率，散射元在方位角上均匀分布，间隔取np=0.5°;考虑距离间隔时，散射元在距离上也服从均匀分布，根据平均能量法，距离间隔为ΔR= cT/2（其中T为发射脉冲宽度）。

根据式（3）的回波模型进行仿真，假定海深100 m，鱼雷航行深度40 m，海况2级;海底为同一种底质（如淤泥、沙底、岩石底等）;分别采用8×1线阵和6× 6平面阵，阵元分布分别如图2和图3所示;发射CW信号，中心频率f0=15 kHz，阵元间隔d=λ/2。图4给出了1组发射脉宽T=50 ms的混响仿真结果，声吸收系数按经验公式α=0.036（f/1000）1.5计算。

3 模型特性分析

3.1 混响时间相关特性

对于CW脉冲，混响的包络在脉冲宽度范围内是相关的［8］，其自相关函数与CW脉冲的自相关函数相近。发射信号脉宽T=50 ms，采样时间为4 s，随机抽取某阵元的仿真数据，并进行统计分析（见图5）。从图5中可知，混响瞬时值自相关函数与理论结果一致。

3.2 混响频率随时间的变化规律

根据散射点模型，可以得到混响的频移量（即散射元的多普勒）为

随着时间t（或者距离r）的变化，fd应成增长趋势。混响仿真时，声呐平台运动速度v=20 kn，随机抽取某阵元的混响数据进行处理。fd与t关系的理论曲线与仿真结果比较如图6所示。从图6可以看出，混响的仿真结果与理论分析相符。

图5 混响时间相关特性Fig.5The temporal-correlation characteristics of reverberation

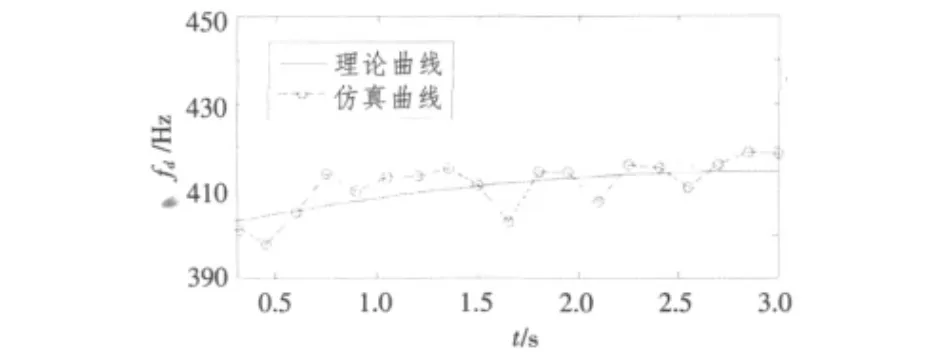
图6 混响中心频率频移量随时间变化规律Fig.6Thecenter frequency with time

3.3 各阵元接收信号相位关系分析

对于界面混响，每个阵元接收的混响信号都是空间各方位角上的散射元回波的叠加，且同一散射元到不同阵元的声程差为dn·sinθm·sinαm/c。对于各水平阵元来讲，各阵元对于每个散射元的声程差是一致的，因此接收信号的相位差应该随时间保持稳定;但对于各垂直阵元来讲，由于同一散射元对不同阵元的θm=cos－1（H/rm）不一致，且随着时间t（距离）增长，因此各垂直阵元间相位差在整个采样时间内应成增长规律。为验证各阵元相位关系，采用6×6平面阵。结果如图7所示，这与以上的理论分析一致。

图7 各阵元接收信号相位差Fig．7The phase difference between receiving signals from multiple-element

3.4 各阵元接收信号空间相关特性验证

所谓混响信号的空间相关性，就是彼此相距一定距离的2个接收点接收到的混响信号之间的相关特性［8－10］。混响信道作为一随机空变信道，文献［9］给出了空间互相关函数的定义:

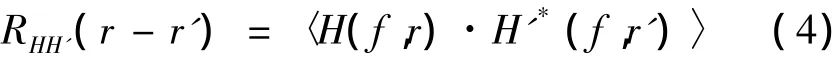
其中，r和r'为2个接收点空间坐标的矢径;H（f，r）和H'（f，r'）为相应参数的混响信号。在各态历经条件下，用时间平均代替统计平均。按接收点空间位置关系，又可分为水平空间关系和垂直空间关系。

为了验证平面阵空间相关性，仿真实验采用6× 6的平面阵（阵元分布见图3），各水平、垂直阵元与第36号阵元间的空间相关系数见图8（其中:采用的水平阵元为6，12，18，24，30，36;垂直阵元为31，32，33，34，35，36）。从图8可以看出，混响仿真信号的空间相关性符合理论分析结果，即混响信号的水平空间相关性随距离的增加衰减很快;而垂直空间相关性随距离的增加衰减较慢［11－13］。

图8 空间相关性Fig.8The spatial relativities

3.5 混响的空时谱

声呐混响的产生机理和部分特性同机载雷达的杂波非常相似，具有空时二维耦合的特性。混响仿真实验采用8×1线阵，考虑到基阵的空间指向性，并为减少计算量，只计算空间方位角－20°～20°范围内的单元散射点。图9为混响仿真数据的功率空时二维谱图。从图9可以看出，混响主要集中在－20°～20°范围内，由于宽带模型的建立以及散射单元内部波动的影响使得混响在空间上有所扩展，这与实际混响特性相符。

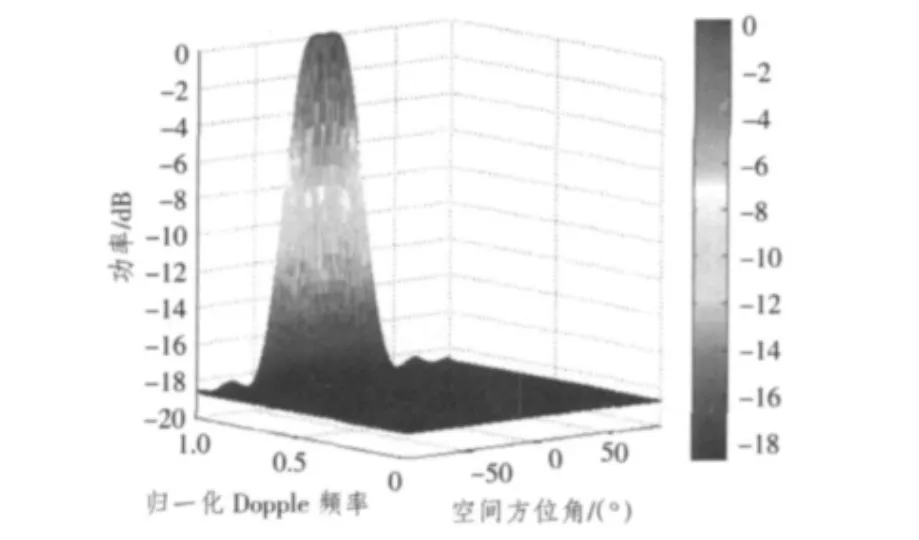
图9 混响功率谱Fig.9The power spectrum of reverberation

4 结语

本文利用散射点的宽带回波原理，考虑多种能对混响产生影响的因素，包括发射信号本身的参数、平台运动的影响、海洋环境参数等，建立了基于单元散射的精细结构混响回波模型。仿真结果表明，该混响模型除了能比较完整细致地模拟混响的各种统计特性外，还能保持阵元间的空间相关性，其混响空－时谱也与理论分析相符。

［1］赵申东，唐劲松，蔡志明．多通道运动声呐混响仿真［J］．舰船科学技术，2007，29（4），117－124．

［2］赵申东，唐劲松，蔡志明．任意阵型混响仿真及检验［J］．武汉理工大学学报（交通科学与工程版），2009，33 （1），173－176．

［3］周晶．运动声呐界面混响仿真研究［J］．舰船电子工程，2010，187，197－200．

［4］CHAMBERLAIN S G，GALLI J C.A model for numerical simulationofnonstationarysonarreverberationusing lineaspectral prediction［J］．IEEE Journal of Oceanic Engineering，1983，8（1）:21－36．

［5］LUBY J C，LYTLEDW.Autoregressivemodelingof nonstationary multibeam sonar reverberation［J］．IEEE Journa of Oceanic Engineering，1983，12（1）:116－129．

［6］徐新盛，张燕，等．海底混响仿真研究［J］．声学学报，1998，23（2），141－148．

［7］朱埜．主动声呐检测信息原理（第一版）［M］．北京:海洋出版社，1990．

［8］B.B．奥里雪夫斯基．海洋混响的统计特性（第一版）［M］．罗耀杰，等译．北京:科学出版社，1997．100－157．

［9］惠俊英，生雪莉．水下声信道（第二版）［M］．北京:国防工业出版社，2007．99－109．

［10］葛凤祥，惠俊英，蔡平，彭应宁．界面混响信号的仿真研究［J］．电子与信息学报，2001，23（12）:1292－1297．

［11］URICK R J，LUND G R．Vertical coherence of shallow water reverberation［J］．J.Acoust.Soc.Am．，1970，47: 342．

［12］URICK R J，LUND G R．Horizontal coherence of explosive reverberation［J］．J.Acoust.Soc.Am．，1970，47:909．

［13］KLEMMR R．Problems of Spatial Signal Processing in ShallowWater.IssuesinAcousticSignal/Image Processing.NATO ASI Series，Vol，FI，Springer Verlag，1983．113－137．