LNG船液舱围护系统结构极限承载力研究

滕蓓，陆晔，祁恩荣

（1．江苏省无锡交通高等职业技术学校，江苏无锡214151; 2．中国船舶科学研究中心，江苏无锡 214082）

0 引言

过去10年间，在LNG船运输过程中晃荡成为一个非常重要的实用性问题。生产的大量LNG运输船与典型的LNG运输船相比，其货舱舱容成倍增加（从138 000 m3到266 000 m3）。LNG运输船最通用的是膜型结构，利用膜型结构的主要原因是LNG运输船能在很低的温度（－163℃）下利用一种复杂的附属在船体结构上绝缘系统来保存液体［1］。

随着LNG运输船尺寸增加，其操作要求也越来越严格。一般来讲，LNG运输船只允许在满载和空舱情况下营运，但是目前有时需要允许部分装载［2－3］。这在设计时对于控制系统和船体连接结构显得相当困难，美国船级社［4］和国际船级社协会［5］对LNG运输船也有不同的设计要求。剧烈的晃荡会直接导致各种冲击影响［6－8］，当增至结构极限载荷时，控制系统和船体结构会遭到毁灭性破坏［9］。因此，对LNG船液舱围护系统极限状态的研究显得尤为重要。

1 大型LNG船液舱围护系统结构特点

1.1 舱室结构特征

在LNG运输时，LNG始终处在常压和－163℃左右的低温条件下，超低温货物要求与货物接触的船舶结构材料具有抵抗低温的能力，因此须采用具有较低热膨胀率的特殊钢材作为船舱内壁建造材料。大型LNG船液舱根据储罐系统不同可分为独立球罐型（MOSS）、SPB型船棱柱型（IHI）和薄膜型（Membrane）3种类型。本论文讨论的是LNG薄膜型围护结构。

薄膜型LNG船的货舱结构见图1，为低温内壁直接由双层外壳支撑，内壁由2层材料相同的金属膜和2个独立的泡沫绝热层组成，包括内薄膜层、绝热层、次屏障薄膜层、绝热层及船体内壳板。薄膜层覆盖的货舱被绝热层、次屏障薄膜层和绝热层包围，并直接与双层船体相连，泡沫绝热层中充满氮气，装有监控器以监控温度和压力。薄膜型船的液货舱按其采用绝热材料和施工方式的不同可分为2种:一种是GTT No．96型，一般使用殷钢为内壁结构，厚度仅为0.7 mm;另一种是MK－Ⅲ型，有绝热层，使用波纹状不锈钢薄膜片为内壁结构，厚度为1 mm。舱内货物重量直接作用在薄膜层上并传递给船舶结构承担，同时薄膜层还要不断受到LNG货物的晃荡冲击，容易发生破损。目前，液舱的装载率可以在舱容的10%以下或70%以上，设置上下限主要是为防止过大的晃荡载荷。

图1 LNG薄膜型液舱典型结构Fig.1Typical LNG structure of member type

1.2 NO．96型LNG船液舱围护系统结构特点

以NO．96型LNG船绝缘层箱型结构承受晃荡冲击载荷为例，液舱由箱型围护系统结构联接而成，1艘15万t LNG船总共需要51 444个箱型结构。

围护系统的结构有2层，长度为1 200 mm，宽度为999 mm，高度为530 mm，如图2所示。分别由2种不同的层合板箱型结构组成。内薄膜层箱型结构有7根纵向隔板，高度为230 mm;第2层箱型结构有6根横向隔板，高度为300 mm。箱体内充满处理过的硅胶绝缘粘体。每种厚度的层合板都由不同层数的板组成，如表1所示。

图2 LNG船液舱围护系统结构Fig.2LNG cargo containment system structure

表1 不同厚度层合板对应的木板层数Tab．1Ply of different thickness plywood

1.3 层合板材料力学性能

薄膜型LNG船的液舱围护系统结构中的层合板的材质是桦木，属于各向异性脆性材料。由于层合板的层数多，故在拉伸试验中表现出的力学性能有所不同（见表2）。弹性范围内材料为正交各向同性，拉伸极限状态时各个方向极限应力有所不同，但断裂应变基本相同，弹性模量亦基本相同。试验表明，单个木材极限破坏之前局部已经有塑性变形，因此结合工程实际情况，本文将层合板均简化为各向同性的弹塑性材料。

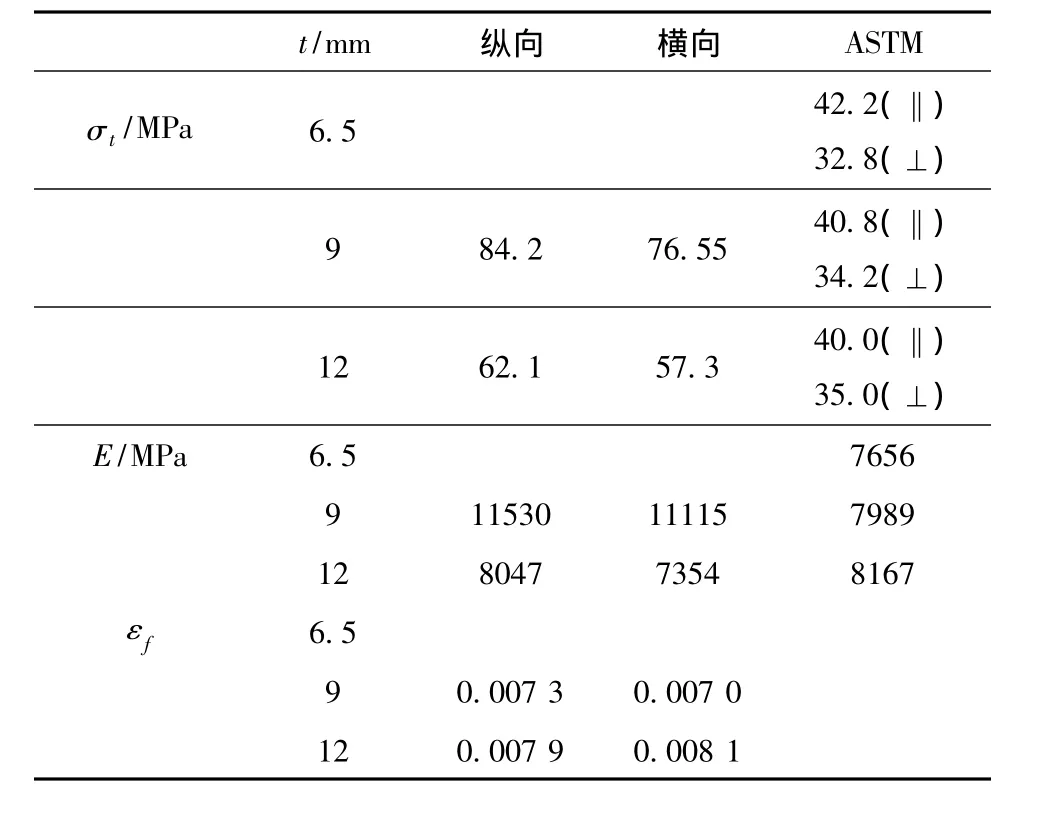
表2 层合板材料力学性能Tab．2Mechanical properties of plywood material obtained by tensile coupon test

215.68万立方LNG船液舱围护系统结构的极限强度

本文利用非线性有限元法计算围护系统结构在静态压力下的极限强度。并且计算不同边界条件的极限强度进行对比分析。

2.13 种边界条件计算结果比较分析

液舱围护系统结构的极限强度采用非线性分析，涉及到几何非线性（大变形）与材料非线性（塑性）。图3为该结构在Ansys中的有限元模型。所有板都采用shell 181壳单元，共划分21 008个单元，最终每个板单元的边长比接近1，为20.812 5×20.357 1 mm。

图3 NO96型围护系统结构有限元模型Fig.3Ansys finite element model for the NO．96 type insulation box structure

在Ansys有限元建模中，材料的弹性模量为E= 7 937 MPa，层合板材料屈服强度σs=25.5 MPa。围护系统结构底面由船体内底板支撑，将其作为刚性板处理，上层板四边界条件为四边自由、四边简支和四边固定。

Ansys的非线性分析类型选为Static（静力/稳态求解），在非线性设置选项中打开Large deform effects （大变形效应）选项，Equation Solver（求解器类型）选为由系统自动选择，激活arc‐length method（弧长法），在计算过程中施加均布载荷3 MPa，子步设为300步。

图4显示的是四边自由边界条件下箱型结构极限状态时隔板的失效模式，第2层箱型结构纵向最外层封板已达到塑性变形，最大位移为9.495 mm，而中间隔板变形很小;最大应力区主要分布在第2层箱型结构的最外层封板上，最大位移出现在第2层箱型结构最外层横隔板上。图5显示的是四边简支边界条件下箱型结构极限状态时隔板的失效模式，第2层箱型结构纵向最外层封板已达到塑性变形，最大位移为9.266 mm，中间隔板也发生屈曲变形;最大应力区主要分布在第2层箱型结构的最外层封板上。最大位移出现在第2层箱型结构最外层横隔板上。图6显示的是四边固定边界条件下箱型结构极限状态时隔板的失效模式，第2层箱型结构纵向最外层封板已和中间隔板均发生较大的塑性变形，且最中间隔板的变形最大，为2.527 mm。图7为3种边界条件下压力与顶板中心位移关系图。表3为3种边界条件下液舱围护系统结构的极限强度比较。

图7 压力与顶板中心位移关系图Fig．7Pressure versus deflection at the center of the top plywood panel

表3 不同边界条件下液舱围护系统结构的极限强度比较Tab．3Compare with ultimate strength of insulation box structure under different conditions

由此可见:不同边界条件下分析围护系统结构静态压力极限强度，第2层箱型结构在承受垂向压力时会首先破坏;由于边界条件的不同会直接影响结构的最终失效模式。

2.2 ABS试验中箱型结构的失效模式

美国船级社（ABS）在2006年做了有关大型LNG船液舱围护系统结构强度的实验，如图8所示。该实验表明:箱型结构在承受垂向压力时的失效模式为第二箱型结构外侧纵向封板首先进入塑性阶段并且崩溃。因此对比本文有限元计算结果，边界条件应选为四边简支最符合实际情况。

图8 ABS试验中箱型结构失效模式Fig.8Deformed shape of the insulation box in ABS test

2.3 各向异性材料板极限强度的理论计算

各向异性材料板的屈服应力公式为:

其中，L为板的长度;B为板的宽度;t为板的厚度;当Ex和μx为x方向板的弹性模量和因x方向伸长在y方向收缩的泊松比，Ey和μy为y方向板的弹性模量和因y方向伸长在x方向收缩的泊松比时，Dx表示板在x方向的弯曲刚度;Dy=表示板在y方向的弯曲刚度;H=表示板的扭转刚度，E1=μx·Ey=μy·Ex;m为屈曲半波数，由1）2决定。

由上式可以看出，当Dx=Dy即材料各向同性时，式（1）有最小值，因此有限元计算采用各向同性材料是可靠的。

3 结语

1）通过对围护系统结构在准静态压力之下极限强度的计算可以发现，第2层箱型结构在承受垂向压力时首先破坏。

2）分析了不同边界条件下的围护系统极限强度，边界条件的不同直接影响了结构最终的失效模式:顶板不受约束达到极限状态时，第2层箱型结构纵向外侧封板首先进入塑性变形，中间隔板变形很小;顶板四周简支达到极限状态时，第2层箱型结构纵向封板和中间隔板均破坏，但是外侧封板变形比隔板大;当顶板四周固定达到极限状态时，第2层箱型结构中间隔板最先崩溃。

3）与理论计算项比较可知:将液舱围护系统结构的材料简化为各向同性弹塑性材料后计算出的结果比实际的各向异性材料更保守，偏于安全，可为液舱围护系统结构设计提供必要依据。

［1］PAIK J K．Limit state design technology for a membrane type liquid natural gas cargo containment system under sloshing impacts［J］．Marine Technology，2006，43（3）:126－134．

［2］ISSC．REPORT of Committee I．2:Loads［A］．Proc of 16 th Int．Ship and Offshore Structures Congress，St John's，2006，1:87－179．

［3］ISSC．REPORT of Committee II．2:Dynamic Response［A］．Proc of 16 th Int．Ship and Offshore Structures Congress，St John's，2006，1:267－367．

［4］ABS．STRENGTHassessmentofmembrane-typeLNG containment systemsundersloshingloads［S］．ABS Guidance Notes，2006．

［5］IACS．COMMON structural rules for double hull oil tanker［S］．IACS Common Structural Rules，2006．

［6］朱仁庆．液体晃荡及其与结构的相互作用［D］．无锡:中国船舶科学研究中心，2001．

ZHU Ren-qing．The interaction between sloshing of liquid and structure［D］．Wuxi:China Ship Scientific Research Center，2001．

［7］王德禹，金咸定，李龙渊．液舱流体晃荡的模型试验［J］．上海交通大学学报，1998，32（11）:114－117．

WANG De-yu，JIN Xian-ding，LI Long-yuan．On model experiment of sloshing intanks［J］．Journal of Shanghai Jiaotong University，1998，32（11）:114－117．

［8］王德禹，李龙渊，施其．三自由度晃荡模拟装置及其模态分析［J］．海洋工程，2000，18（4）:94－96．

WANG De-yu，LI Long-yuan，SHI Qi．Three freedom solshing simulator and its model analysis［J］．Ocean Engineering，2000，18（4）:94－96．

［9］祁恩荣，崔维成．破损船体极限强度非线性有限元分析［J］．船舶力学，2005，9（5）:83－91．

QI En-rong，CUI Wei-cheng．Nonlinear finite element analysis of ultimate strength of damaged ship hulls［J］．Journal of Ship Mechanics，2005，9（5）:83－91．