弹地人在回路末制导时延补偿改进模型

刘冬，鲜勇，胡真坚，杨得国，郭飞帅

(第二炮兵工程大学603教研室，陕西西安 710025)

引言

某新型巡航导弹拥有了卫星通信链路的支持，可以实现人在回路的作战应用。然而，导弹弹上成像传感器摄取图像后经图像解压缩、数据加解密、卫星上下传、地面处理、人工操作、导弹制导控制运算等一系列过程，到最终导弹形成制导指令，比一般应用在战术导弹/炸弹的电视制导方式需要更长的时间。因此，研究地面目标指示信息时间延迟情况下的末段精确制导技术是实现巡航导弹人在回路精确制导的基础。

国外在人在回路制导控制延迟补偿技术方面已经比较成熟，如美国海军的战斧Block-IV，俄罗斯Π-700“花岗岩”超声速反舰巡航导弹等都达到了先进水平。虽然国内在空投激光导引炸弹、激光导引空空导弹、人工导引反坦克导弹等方面取得了丰硕成果，武器的打击精度和战场适应能力得到了大幅度提高，但是对于远程巡航导弹目前仍然处于发射后不管的作战模式，远程巡航导弹的人在回路控制、大延时精确制导方面尚处于理论研究的初级阶段［1-8］。

1 人在回路时延补偿问题的提出

惯性导航系统是巡航导弹制导的基础，具有短时精度高、信息全面、数据更新率高的特点。但惯性导航系统误差具有随时间积累的特性，导航时间越长，导航误差越大，必须依靠卫星导航、地形匹配和景像匹配进行修正。

末制导时，导弹以惯性导航系统为主，依靠前视导引头提供目标与导弹的相对关系，形成制导指令，消除制导误差。当不存在目标指示信息延迟情况时，导弹可以直接利用导引头信号进行精确制导。当存在目标指示信息延迟后，必须对延迟造成的状态误差进行修正。

利用时间截获得时间间隔Δt;利用惯性导航系统短时导航精度高的特点，建立惯性系统相对导航模型，在运动学模型的基础上解算导弹在t时刻和t+Δt时刻的相对状态关系;依据导弹在t时刻目标在导引头视场内的信息、相对导航信息的基础上解算导弹在t+Δt时刻的导引量，为精确制导提供导引指令。基于上述补偿思想，本文提出了小量近似法及双重定位法两种补偿方案。

2 弹地人在回路时延补偿方法

本文提出几点假设:

(1)当导弹进入末制导阶段后，导弹在没有收到地面导引指令前将沿直线飞行;

(2)由于惯导短时精度高，所以惯导测出Δt时间内的导弹相对位置距离等于导弹真实的相对位置距离;

(3)在惯性坐标系下仅推导导弹与目标横向关系，纵向导引量计算方法类似，不再叙述。

2.1 小量近似法

图1 惯性坐标系下横向位置关系图

建立模型如下:

导弹t时刻回传信息至地面与t+Δt时刻收到目标的指示信息之间的延迟大约为0.1～1.0 s之间，所以可以将看成小量，从而得到≈α。

如图1所示，可得到近似公式如下:

从图1中解算三角形几何关系，可求得t+Δt时刻导弹所需要的横向导引量为:

2.2 双重定位法

图2 双重定位法横向位置关系图

双重定位法横向位置关系见图2。图中，t1，t2，t3都是以导弹上惯导输出的时间为基准(地面上收到的图像信息是实时更新的，以导弹惯导时间为基准有利于计算);(x1，y1，z1)，(x2，y2，z2)，(x3，y3，z3)分别为t1，t2，t3时刻导弹惯导测出的坐标;L为t3时刻惯导求得的导弹与目标的距离;分别为t1，t2时刻的横向导引量为t2和t1时刻导弹真实位置的相对距离;s1为t2和t1时刻导弹惯导位置的相对距离;为t3和t2时刻导弹真实位置的相对距离;s2为t3和t2时刻导弹惯导位置的相对距离;为t3时刻导弹在导引头视场中心线上的位置与垂直视准线且经过目标纵平面的距离。

导弹获取目标视图后，通过数据链将导弹的导航信息及目标图像回传至地面指挥中心。地面通过多功能显示器，实时显示出导引头视场信息。捕控手通过实时画面，人工识别目标并在t1时刻对目标进行预锁定，并通过数据链将导弹t1时刻的惯性导航数据及目标的指示信息于t1+Δt(Δt即为时间延迟)时刻回传至弹上并记录其信息(x1，y1，z1，φ1，t1)。经过时间Δt1(Δt1=t2－t1)，捕控手在t2时刻对攻击目标进行二次确认并通过数据链将导弹t2时刻的惯性导航数据及目标的指示信息(x2，y2，z2，φ2，t2)于t3时刻(t3=t2+Δt)回传至弹上。同时记录下导弹t3时刻的导航信息(x3，y3，z3)，从而解算出此刻导弹相应的导引控制量φ3。

从图2中解算三角形几何关系得:

通过惯导可以解算出t3时刻导弹与目标的距离L，则惯导测量误差为Δs=L－

2.3 仿真及结果分析

双重定位法中人在第二次锁定目标时，由于人为抖动等因素会出现偏差，使得前后两次所选的目标不在同一个位置，从而最终影响其制导精度。文献［4］中指出:由于人工操控抖动引起的噪声为有限带宽的白噪声，幅度为输入偏差量的5%。

用MATLAB/Simulink进行了仿真。仿真条件如下:导弹初始导引量=3°，速度v=250 m/s，时间延迟Δt=1 s，预锁定到最终锁定目标时间间隔Δt1=2 s，人为抖动偏差量为5%，给定初始导弹惯导测量位置离目标的距离为20 km，惯性测量误差为1 km。

当惯性测量距离s5不变时，随着导弹初始导引量的变化，目标横向位置误差的变化曲线如图3所示。当不变时，导目真实距离与目标横向误差关系如图4所示。利用双重定位法来解算惯导的测量误差Δs，其关系如图5所示。

图3 导弹初始导引量与目标位置横向误差关系图

图4 导目真实距离与目标横向误差关系图

图5 导目真实距离与惯导测量误差关系图

由图3可以发现，随着导弹初始导引量的增大，目标点的横向误差也会随着增大。所以，在实际应用中如果初始横向导引角度越小，则经过延迟补偿之后目标横向误差会明显变小。小量近似补偿法的效果要优于另外两种方法，双重定位法中由于第二次人为抖动等的原因会影响落点偏差。

从图4可以看出，经过小量近似法延迟补偿之后，目标横向精度有显著提高;小量近似法的精度要明显优于双重定位法。双重定位法虽然误差较大，但却能解算出惯导测量误差Δs，且随着距离的减小有收敛的趋势，这将为后续方法的改进提供一个重要的信息参考量。

从图5可以看到，随着距离的减小，解算得到的惯导测量误差趋于收敛。

3 弹地人在回路改进时延补偿方法

3.1 双重定位+小量近似补偿改进法

当导弹与目标距离小于2 km时，小量近似时延补偿法随着距离的减小，惯导测量误差对精度的影响比重会越来越大，从而导致目标横向偏差增大(如图4所示)。因此，当导弹接近目标2 km时，可以通过双重定位法先解算出惯导测量误差Δs后再去修正小量近似法，从而进一步提高导弹精度。仿真条件按2.3节不变，仿真结果如图6所示。

图6 导目真实距离与目标横向误差关系图

从图6可以得到，当导目真实距离在2 km以下时，利用双重定位+小量近似法误差有明显下降。当导目真实距离在800 m以下时，不再进行双重定位法修正，主要考虑以下原因:双重定位法中预锁定+传输延迟时间在仿真计算中需要3 s，即大约需要750 m的方法解算距离，所以在800 m以下时使用双重定位法解算出Δs后已经没有实际意义，且Δs估算偏差有放大和突变趋势。

通过大量的仿真实验发现，导弹的最佳实施距离范围为1～2 km，在该范围内利用双重定位法+小量近似法解算出相应的导引量，导弹的落点精度有明显提高。如果将锁定时间由2 s增加到3 s，通过仿真会发现最佳实施距离范围在原有基础上幅度变宽。

3.2 二次修订法

对于小量近似补偿法来说，经过一次人在回路可控时延补偿后再进行第二次人在回路可控时延补偿，会发现可控制导的精度会显著提高。原因如下:(1)经过第一次人在回路可控时延补偿后，虽有误差但却可以明显减小第二次人在回路可控时延补偿的初始导引量;(2)由图3可见，初始导引量越小，惯导误差对目标横向误差的影响比重将会减小。

仿真条件不变，经过二次修订后的仿真结果如图7所示。

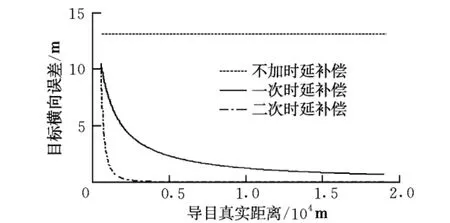
图7 二次修订的仿真结果

上述两种补偿改进方案各有优缺点，也都有各自适用的条件，但精度都是令人满意的。双重定位+小量近似补偿改进法可以算出惯导测量误差Δs，它不仅对时延补偿有益，而且对末制导中导弹的定位、评估、导航等方面都将有所帮助。二次修订法的操作简便，通过减小初始导引量进而减小惯导测量误差对目标横向误差的影响比重，虽然精度有较大提高，但是却没有估算出惯导测量误差。

4 结束语

本文建立了两种弹地人在回路精确末制导时延补偿模型方法和两种改进措施，并根据假设条件进行了仿真，得出加入延迟补偿之后的目标横向误差与初始导引量和距离的关系并进行了分析。在一定范围内，该模型可以在满足一定精度要求下对导引量进行时延补偿。本仿真模型的一些假设条件离实际还有一定的差别，但是却提供了一种解决问题的思路，对下一步的工程实践具有指导和借鉴作用。

［1］ 李欣，郑志强，李鹏，等.时间延迟对电视指令制导系统稳定回路的影响［J］.航空兵器，2010，(5):30-32.

［2］ 宋福志.ATR与人在回路的选择［J］.战术导弹技术，2006，(2):59-62.

［3］ 陈达立，周法强，吴艳滨.人在回路的电视末制导数学建模研究［J］.弹箭与制导学报，2005，25(1):329-331.

［4］ 江洋溢，高士英，刘勤.数据链延迟对捕控指令电视末制导精度的影响［J］.弹箭与制导学报，2004，24(1):118-120.

［5］ 吴森堂，姜智超，张淼.超音速反舰导弹人在回路的电视末制导系统仿真分析研究［J］.航天控制，2003，21(4):18-24.

［6］ 韩统，吴别林，魏贤智，等.时间延迟对电视末制导系统稳定性的影响［J］.火力与指挥控制，2006，31(1):38-40.

［7］ 姜百汇，米小川，游志成.数据链技术在国外飞航导弹上的应用［J］.飞航导弹，2008，(8):30-33.

［8］ William H L.Automatic target recognition(ATR)beyond the year 2000——technologies for future precision strike missile systems［Z］.France:RTO/NATO，2001.