高超声速飞行器一体化纵向气动特性分析
张栋,唐硕,李世珍
(西北工业大学航天飞行动力学技术重点试验室,陕西西安 710072)
引言
高超声速技术具有前瞻性、战略性和带动性,其发展将为航空航天技术带来革命性的突破[1]。美国的X-43A是典型的吸气式高超声速飞行器,机体/推进高度一体化。前体作为超燃冲压发动机的预压缩系统,为进气道提供压缩后的均匀自由流;后体下表面承担发动机排气系统的膨胀功能,同时发动机的推进系统不仅提供克服飞行器阻力的功能,而且一部分动力要为飞行器提供升力。
文献[2]用CFD优化设计乘波体构型的高超声速飞行器,基于CFD研究了机体/推进一体化,并计算了稳定性导数及控制导数。文献[3]利用斜激波理论及普朗特迈耶公式计算了气动力和推力,并且对弹性影响进行分析,基于拉格朗日方程建立了高超声速飞行器的纵向运动模型。文献[4]采用高超声速飞行器几何外形,其前体具有三楔角压缩,即对自由来流的三级压缩。然后基于此外形进行气动力与推力的计算。文献[5]从乘波体飞行器优化设计的角度出发,基于高超声速空气动力学理论计算了纵向气动力及其推力。
但是在上述研究中,对于高超声速飞行器整体气动的计算却存在着不足之处,表现在:文献[3]中没有考虑前体的多级压缩激波影响,近似为一道激波进行计算。文献[4]中,作者仅考虑了前体下表面的三楔角压缩,而忽略了内压段的多级压缩。文献[5]中,作者没有考虑发动机内喷管,直接把燃烧室的出口参数作为后体/外喷管的入口参数,并且没有考虑剪切层(Shear Layer)对气动和推进的影响,这样计算得到的压强很不准确,从而不能准确地计算发动机推力及其气动力。
1 高超声速飞行器几何外形
本文针对引言中提到的不足之处,采用了如图1所示的吸气式高超声速飞行器机体/推进一体化构型,其中Ly,Ln,Lf,Lw表示各段的长度。机身前端采用三级压缩,内压缩段采用两楔角压缩,从而减少了总压损失,为进气道提供了均匀的压缩流。本文假设自由来流为理想气体[3],空气比热比为 γ=1.4,采用三角面元[6-7]逼近机体表面。

图1 吸气式高超声速机体/推进一体化几何外形简图
2 高超声速飞行器上表面压强
根据普朗特迈耶公式推导得出用于高超声速飞行器背风面压力系数计算公式为:
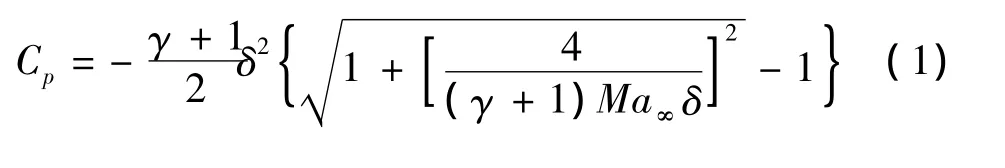
式中,δ为碰撞角;Ma∞为自由来流马赫数。
3 超燃冲压发动机模型
超燃冲压发动机即冲压发动机燃烧室入口气流速度为超声速,燃烧室在超声速气流中进行,由进气道、隔离段、燃烧室和尾喷管构成。没有压气机和涡轮等旋转部件,高速迎面气流经过进气道减速增压,直接进入燃烧室与燃料混合燃烧,产生高温燃气经尾喷管膨胀加速后排出从而产生推力。可将超燃冲压发动机分为前体/进气道、扩散段、隔离段、燃烧室、内喷管和后体/外喷管。隔离段的主要作用是均匀进入燃烧室入口的气流,并使得进气道出口和燃烧室进口的压力匹配。本文认为气流参数通过隔离段不发生变化,工作是理想状态,采用图2所示的超燃冲压发动机简图。

图2 超燃冲压发动机横截面简图
图中,Ai(i=1,2,3,e)表示各个部件的面积;ΔT0为燃料燃烧所引起的总温增量。
3.1 前体/进气道
外压段采用三楔角压缩,内压段两楔角压缩,δi,θi分别表示气流转折角和激波角(i=1,2,3,4,5)。对于多级楔形压缩,各级激波后气体参数可以由式(2)~式(5)确定[5]。

3.2 扩散段
发动机扩散段的出口参数作为燃烧室的入口参数,应用连续方程确定扩散段出口处的马赫数、压力和温度关系[3]:
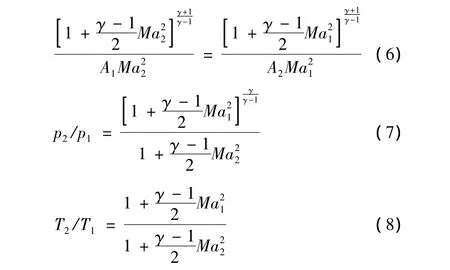
3.3 燃烧室
燃烧室为等截面积,燃烧室出口马赫数、压力和温度采用如下公式计算[3]:
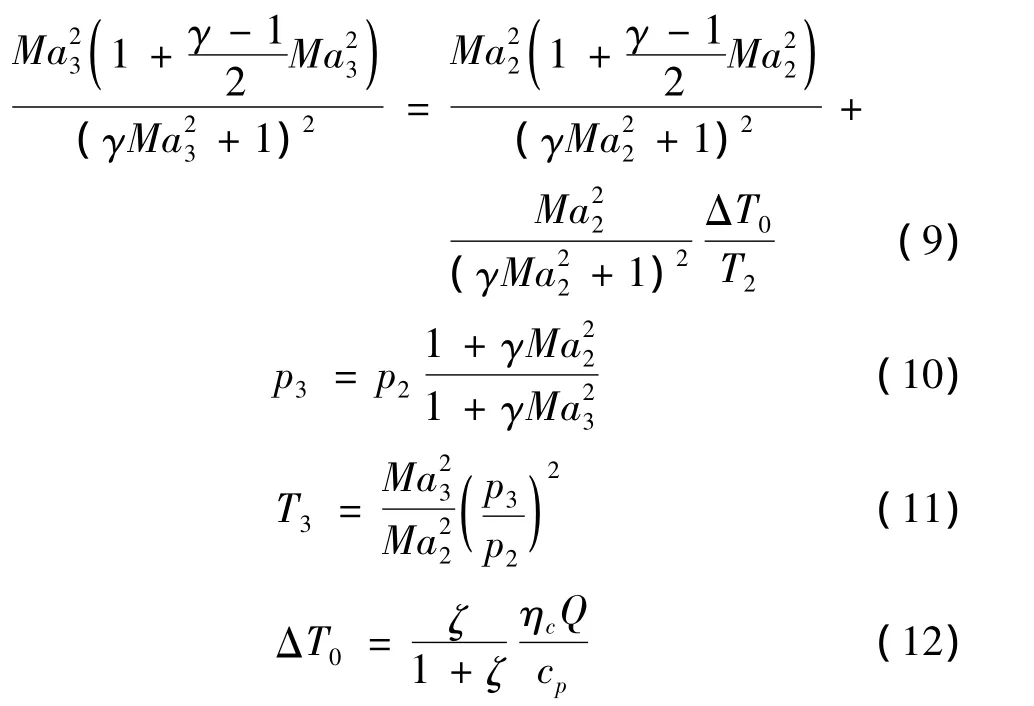
式中,ζ为发动机燃料流速与通过燃烧室的空气流速之比;ηc为燃烧效率;Q为燃料的热值;cp为燃料空气混合气体在常压下的比值。
3.4 内喷管
内喷管中气流的流动是一个非常复杂的三维流动。本文基于准一维流理论对其简化,下面给出马赫数、压力及温度的计算表达式:
2)统计x=1的直线与方块苗文二维表达式f(x)的交点个数rx1,统计x=2直线与f(x)的交点个数rx2,依次循环,直到统计到rx130停止。

3.5 后体/外喷管
燃气流经过内喷管膨胀后,作用在飞行器后体下表面产生压力。后体成为超燃冲压发动机外喷管的上表面,燃气流与自由流间相互作用形成的剪切层作为超燃冲压发动机外喷管的下表面。计算后体下表面的压力首先要确定剪切层的位置,文献[3]给出了后体压力计算公式,通过计算验证了该公式有足够的准确度。

式中,s为外喷管起点沿外喷管方向到外喷管终点的距离。
3.6 发动机推力计算
发动机推力是通过动量定理计算。本文选择了发动机进气道入口处气流的状态与内喷管出口处气流的状态,应用动量定理计算推力。计算公式如下:
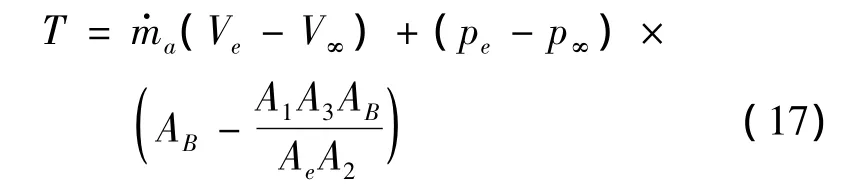
式中,AB=Ae/b为单位出口面积;为质量流量率。
当燃气流通过后体/外喷管时,又一次膨胀产生一部分推力,这部分推力主要是平衡前体产生的阻力,这部分推力的计算在2.5节后体/外喷管的讨论中已经给出。
3.7 控制面压强计算
对于飞行器控制面,文中根据其迎风与背风情况分别采用切楔/切锥法、膨胀波法[8]计算压力系数。
迎风面压力系数计算公式为:

3.8 粘性阻力的计算
上述计算过程是基于无粘性流理论,要更加准确地计算阻力,应该考虑粘性的影响。粘性阻力中比重比较大的是摩擦阻力和底阻,文中采用经验公式计算摩擦阻力和机身底部阻力(低阻)[5]。
粘性阻力系数为:


4 吸气式高超声速飞行器纵向气动特性分析
4.1 CFD比较验证计算精度
为了验证文中计算结果的准确性与有效性,将计算结果与CFD的计算结果(CFD结果来源于课题组CFD计算)进行了比较,如图3所示。由图可知,在考虑了粘性摩擦阻力,发动机关闭时,文中计算的结果与CFD计算结果的变化趋势一致,两者之间的最大误差不超过0.2%,可见本文计算方法有一定的准确性,能够满足吸气式高超声速飞行器的概念研究和初步设计阶段的要求。

图3 与CFD结果比较
4.2 纵向气动特性分析
高超声速飞行器的气动特性是确定其气动外形、飞行轨道和飞行性能的先决条件,基于高超声速空气动力学理论对机身/超燃冲压发动机一体化的气动快速计算,在飞行器的预先研究和优化设计阶段非常重要。
参考国内外的吸气式高超声速飞行器资料并借鉴美国Hyper-X系列,文中设飞行条件为H=30 km,Ma={5,6,7,8},迎角变化 α ={-2°~6°},间隔为2°,舵偏角取为0°,发动机宽度为0.6 m,发动机进气道高度为0.1 m,飞行器总质量为830 kg。图4为Ma=6时发动机开关闭状态下的气动力系数对比。

图4 气动力系数对比曲线
从图中可以看出,发动机工作时有较高的升力系数,主要是由于燃气流作用后体/外喷管产生的附加升力。当迎角大于4°时,发动机工作状态的阻力系数远大于发动机通气状态的阻力系数,主要原因有:(1)发动机通气状态的气动力是通过无粘流理论计算,没有计算粘性阻力的影响,而发动机工作时,增加了粘性阻力;(2)后体/外喷管产生的附加阻力。
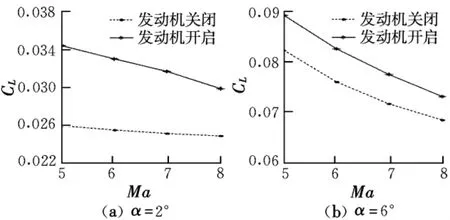
图5 发动机开关闭时气动力系数随马赫数的变化
图5为发动机开关闭时气动力系数随马赫数的变化曲线。由图可知,升力系数随着马赫数的增大而减小,迎角为6°时,升力系数下降幅度较大,其原因可以通过分析后体/外喷管升力系数计算公式得到:CL=CNcosα -CAsinα,其中CN,CA分别为法向力系数、轴向力系数。显然,当迎角增大时,升力系数将减小。
图6为燃油当量比对纵向气动力系数及其推力系数的影响。横轴为燃油当量比、纵轴分别为推力系数、俯仰力矩系数、升阻力系数,其中迎角为2°,马赫数为6。由图可知,随着燃油当量比的增加,升力系数与阻力系数的变化趋势相反。即升力系数增加时,阻力系数减小,反之亦然。燃油当量比对俯仰力矩的影响更明显,主要是因为随着燃油当量比的变化,压心位置变化所致。

图6 燃油当量比对纵向气动力及其推力的影响
5 结束语
由于高超声速飞行器采用了机体/推进一体化构型设计,不能通过常规的气动分析方法进行分析。本文基于高超声速空气动力学理论,采用一体化的思想进行气动计算,并且对某型吸气式高超声速飞行器纵向运动气动特性进行分析。其分析结果表明,该方法不但能快速计算气动力,而且还能较准确地模拟发动机工作时的气动特性。对于高超声速飞行器概念研究和初步设计阶段有一定的参考价值,而且有助于今后进一步研究高超声速飞行器动力学建模、稳定性能和控制系统的设计。
[1] 王鑫,闫杰.升力体构型高超声速飞行器模态稳定性分析[J].西北工业大学学报,2010,28(3):327-331.
[2] Von Eggers Rudd,Pines D.Integrated propulsion effects on the dynamic stability and control of hypersonic waveriders[R].AIAA-2000-2826,2000.
[3] Mirchael A Bolender,David BDoman.A non-linearmodel for the longitudinal dynamics of a hypersonic air-breathing vehicle[R].AIAA-2005-6255,2005.
[4] 刘燕斌,陆宇平.面向控制的高超声速飞行器气动力与动力学一体化的建模新方法[J].计算力学学报,2011,28(1):31-36.
[5] 车竞.高超声速飞行器乘波布局优化设计研究[D].西安:西北工业大学,2006.
[6] Che Jing,Tang Shuo.The engineering calcuation method of aerodynamics of quasi-waverider[J].Acta Aerodynamica Sinica,2007,25(3):381-385.
[7] 徐敏,严恒元.高超声速飞行器空气动力学工程计算方法[M].西安:西北工业大学出版社,1998.
[8] 黄志澄.高超声速飞行器空气动力学[M].北京:国防工业出版社,1995.

