控制器非线性对飞机纵向飞行品质的影响分析

侯建伟，谭文倩，屈香菊

(北京航空航天大学航空科学与工程学院，北京 100191)

引言

在飞控系统设计中，目前广泛采用的是针对线性被控对象的设计技术和设计准则［1］。在实际飞控系统中，传感器和执行机构非线性因素普遍存在，例如静摩擦、机械磁滞、间隙、速率饱和等。没有理想的线性系统，任何一个实际的控制系统，其组成元件总是或多或少地带有非线性特征。非线性造成的结果以噪声的形式在回路中传播，可能会改变系统的相位和阻尼，从而对系统的动态精度产生影响，还可能影响稳定性或引起振荡。研究非线性环节对系统的影响，可以为更合理地设计控制系统提供依据，提高飞机的飞行品质。

在飞机控制器非线性研究领域中，引起较多关注的是速率饱和诱发的PIO事故，且大多使用描述函数法分析系统的稳定性，并给出了评价准则［2-4］，对其它非线性环节的研究较少。并且，非线性描述函数法虽然在工程上得到广泛的应用，但实际上也是线性系统频域计算的近似，并不能完全准确地反映原系统特性。而时域仿真则充分利用了现代计算机的高速计算能力，可以对非线性系统进行直观且足够准确的仿真。

本文基于Chalk飞行品质准则，分析死区、间隙和速率饱和等控制器非线性对飞机纵向短周期特性的影响。选择三种不同的飞控系统构型，研究它们对非线性特性的敏感程度。

1 Chalk准则描述

1.1 准则适用条件

研究控制器非线性特性时，采用频域准则通常比较困难。MIL-STD-1797A飞行品质规范基于大量实验数据，提出了几种应用时域响应结果确定飞机飞行品质的时域准则。Chalk准则就是其中之一，它根据俯仰角速率对驾驶员指令的反应特性评价飞机短周期响应特性［5］。

Chalk准则适用于呈现常规动态模态的飞机和大多数俯仰增益系统。当长周期或其它低频模态的剩余振荡影响俯仰速率时，可略去速度变化的影响，用等速条件下的运动方程组计算俯仰速率瞬态响应。

1.2 飞行品质指标

根据俯仰速率时间响应曲线(见图1)按如下步骤确定Chalk飞行品质指标参数。

图1 对俯仰操纵阶跃输入的俯仰速率响应

(1)确定俯仰速率响应的稳态线;

(2)在俯仰速率响应曲线的最大斜率点上画切线，并与稳态线和时间轴相交;

(3)将从阶跃输入瞬间至最大斜率线与时间轴交点所对应的时间间隔定义为t1，反映飞机响应的时间延迟;

(4)将从阶跃输入瞬间至最大斜率线与稳态线交点所对应的时间间隔定义为t2，反映飞机响应的快速性;

(5)定义Δq1为最大俯仰角速率减去稳态值，定义Δq2为稳态值减去第一个最小值。比值Δq2/Δq1反映飞机响应的平稳性，其值越小，说明系统越平稳。

Chalk准则指标规定如下:

(1)有效时间延迟t1:对于位移或力操纵系统分别采用阶跃位移偏度或阶跃操纵力，t1的限制值如表1所示。

(2)瞬态峰值比Δq2/Δq1:为了确保短周期的足够阻尼或俯仰反应的主模态，Δq2/Δq1应在表1所示的限制要求之内。

(3)有效上升时间Δt:有效上升时间定义为Δt=t2－t1，应是如表2所示限制值中的一个，其中VT为真速。

表1 t1和Δq2/Δq1的限制值

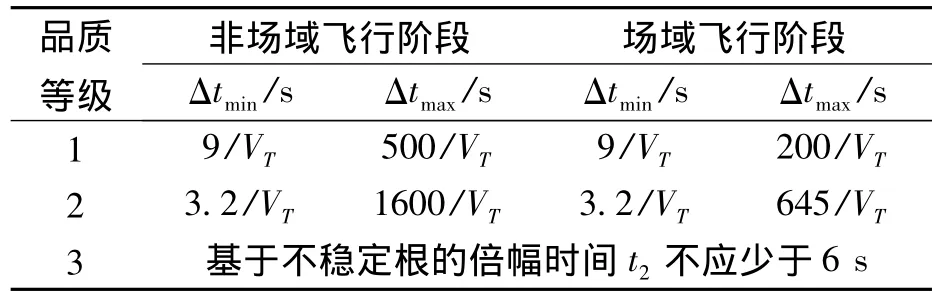
表2 Δt的限制值

2 非线性飞机模型建立

2.1 线性飞机本体模型

本文采用文献［6］给出的某机纵向二阶小扰动线化模型，基准运动状态取为定直平飞。飞机状态方程为x·=Ax+Bu，其中状态变量为x=［αq］T;控制变量为u=δe;状态矩阵和控制矩阵为:

由于该飞机本体模型不稳定，采用了CAS控制系统构型设计，系统结构如图2所示，对于线性系统应除去图中的非线性环节。

图2 CAS飞控系统模型结构

表3给出了本文研究的三种不同的CAS飞控系统模型及相应的Chalk准则飞行品质评价结果。

表3 三种飞控系统模型及飞行品质评价结果

2.2 非线性飞控系统模型

包含死区、间隙或速率饱和等非线性环节的CAS飞控系统模型如图2所示。下面分别讨论各个非线性环节的模型及其特性。

2.2.1死区

控制系统中的死区包括测量元件、放大器和执行机构的死区等。当输入信号在零值附近的一个小范围内时，并没有有用的信号输出;只有当输入信号大于这个范围时，才输出有用信号使系统工作。这个零值附近的小信号范围便是死区。执行机构上的静摩擦力矩往往可以折合为死区，只有当误差引起的执行机构转矩恰好等于静摩擦力矩时，输出轴才开始转动。死区的数学表达式为:

式中，d为死区的大小;x1和x2分别为输入和输出。

2.2.2间隙

传动机构的间隙是控制系统中一种常见的非线性环节，通常发生在包含联动装置或者具有有限间隙的齿轮的所有机械系统中。连杆机构中主动杆与从动杆连接存在空隙。在主动杆输入小于一定值时，从动杆没有任何响应。这和死区有些类似，但间隙的响应与输入的方向有关系，被称为“移动的死区”。间隙特性的典型形式如图3所示(数学表达式见式(2))。

图3 间隙非线性示意图

式中，b为间隙的大小;K为间隙的斜率。

间隙对系统性能的影响比较复杂。一般来说，它会增大系统的静差，使系统波形失真，过渡过程振荡加剧。通过分析间隙的频率特性可知，间隙使输出量在相角上产生滞后，从而使系统的性能变坏，甚至引起自激振荡。间隙引起振荡的原因，直观上来说是由于传动机构在越过间隙区时相当于空载，此时系统能量消耗减少，使得在越过间隙之后再重新带动负载时的总能量增大，因而会使系统的振荡加剧［4］。

2.2.3速率饱和

饱和特性是常见的一种非线性环节。舵机的转速ω随着控制电压的增长而线性增长，当控制电压超过一定数值时，转速增高缓慢从而出现饱和，因此舵机的功率限制就表现为转速呈饱和特性。理想的饱和特性的数学表达形式为:

式中，a为速率饱和限制值，a值越小，说明速率饱和限制越厉害。饱和特性的存在相当于大信号作用时，增益下降。即在线性范围内增益为1，而在饱和区，虽然输入信号继续增大而输出却保持不变。

图4给出了考虑速率饱和环节的飞机-舵机系统结构图，其中舵机取为二阶环节形式，ωn=30 rad/s，ξn=0.707。图中，δc代表指令舵偏，δr代表实际舵偏。

图4 包含速率饱和环节的飞机模型结构

3 死区对飞行品质的影响分析

将图2中的非线性环节表示成死区，计算单位阶跃输入下系统的输出。飞机构型Ⅰ的俯仰角速度时域响应曲线如图5所示。由图可知，死区d值较小时，飞机有效时间延迟t1为0，即俯仰角速度曲线斜率最大点在t=0处。随着d的增大，t1也增加。

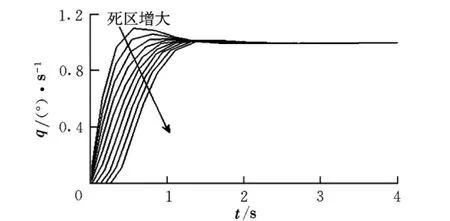
图5 含死区的俯仰角速度阶跃响应(构型Ⅰ)

3.1 有效时间延迟t1

对表3给出的三种飞机构型时域仿真结果进行Chalk准则飞行品质评价，t1的计算结果如图6所示。

图6 死区大小对有效时间延迟的影响

由图可知，死区d值越大，t1越大。对于构型Ⅰ，当d≤0.5°时，飞机呈现1级飞行品质;d=0.6°时为2级飞行品质;d＞0.6°后为3级飞行品质。比较构型Ⅰ，Ⅱ和Ⅲ的计算结果可知，当线性构型的t1略有增加时，随着d的增加，t1大幅增加。对构型Ⅱ和Ⅲ，当d＞0.1°时，飞行品质就达到3级。可见包含死区的非线性系统有效时间延迟对原线性系统的t1值非常敏感。

3.2 瞬态峰值比Δq2/Δq1

瞬态峰值比的计算结果如图7所示。由图可知，对于构型Ⅰ和Ⅱ，随着d的增大，Δq2/Δq1略有减小，系统阻尼略微增加，有利于系统平稳。由于原线性系统本身就具有1级飞行品质，死区对该参数的影响是有利的，因此加入死区后系统仍处于1级飞行品质。对于构型Ⅲ，Δq2/Δq1在d≥0.1°时有较大增加，但仍属1级飞行品质。

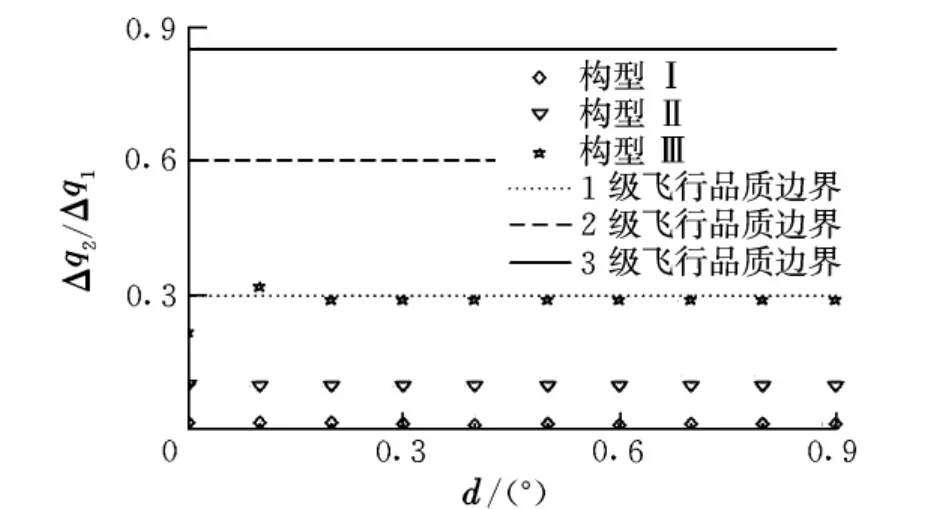
图7 死区大小对瞬态峰值比的影响

3.3 有效上升时间Δt

Δt的计算结果如图8所示。由图可知，对于构型Ⅰ，Δt随d的增大而增大，当d≥0.5°时，Δt的增加趋势变平缓，飞行品质处于1级飞行品质边界。对于构型Ⅱ和Ⅲ，当d＞0.1°时Δt的变化就已经不明显了，此时进入2级飞行品质边界。这是由于原线性系统Δt本身已接近2级飞行品质边界的缘故。总之，死区使得系统快速性变差。

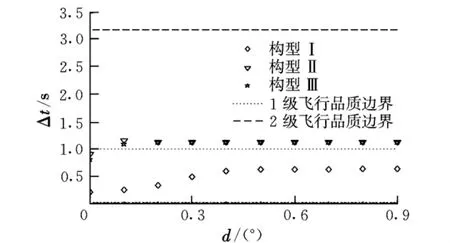
图8 死区大小对有效上升时间的影响

4 间隙对飞行品质的影响分析

飞机构型Ⅰ的俯仰角速度阶跃响应曲线如图9所示。由图可知，间隙b增加可能导致系统出现自激振荡。随着b的增加，振荡幅值也增加，但振荡的频率没有明显变化。

4.1 有效时间延迟t1

有效时间延迟的计算结果如图10所示。由图可知，对于构型Ⅰ，t1随b的增加变化很小，飞行品质始终属1级。比较构型Ⅰ，Ⅱ和Ⅲ的计算结果，当线性构型的t1略有增加时，t1随b的增加而大幅增加。对于构型Ⅱ和Ⅲ，当b≥0.3°时，飞行品质就已达到3级。可见包含间隙的非线性系统的t1对原线性系统的t1值非常敏感。此分析结果与死区非线性的影响一致。

4.2 瞬态峰值比Δq2/Δq1

瞬态峰值比的计算结果如图11所示。由图可知，b越大，Δq2/Δq1越大，系统阻尼特性越差，这严重影响了系统的平稳性。对于构型Ⅰ，当b≥0.2°时，达到2级飞行品质;当b≥0.5°时，达到3级飞行品质。对于构型Ⅱ和Ⅲ，当b＞0.1°时，达到3级飞行品质。

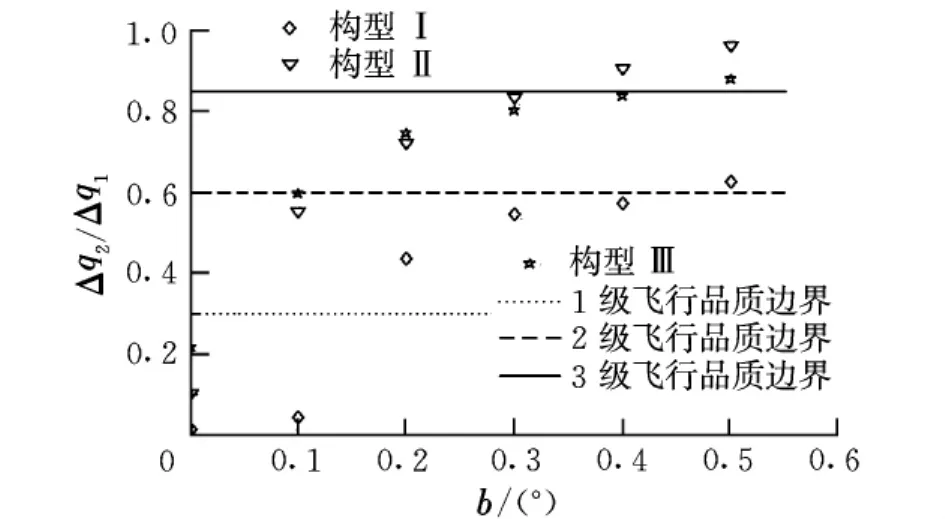
图11 间隙大小对瞬态峰值比的影响

4.3 有效上升时间Δt

有效上升时间的计算结果如图12所示。由图可知，对于构型Ⅰ，随着b的增大，Δt也增大，但该指标始终处于1级飞行品质边界内。对于构型Ⅱ和Ⅲ，由于原线性系统的Δt已接近2级飞行品质边界，因此当b=0.1°时，达到2级飞行品质。

图12 间隙大小对有效上升时间的影响

5 速率饱和对飞行品质的影响分析

飞机构型Ⅰ的俯仰角速度阶跃响应曲线如图13所示，图中箭头指示速率饱和限制值a增大的方向。由图可知，速率饱和非线性使得系统出现了明显的相位滞后。

图13 含速率饱和的俯仰角速度阶跃响应(构型Ⅰ)

5.1 有效时间延迟t1

有效时间延迟的计算结果如图14所示。由图可知，a越小，t1越大，系统性能越差。对于构型Ⅰ，当a＞1(°)/s时，飞行品质为1级;a≤1(°)/s时，飞行品质为3级。对于构型Ⅱ和Ⅲ，飞行品质始终处于1级边界内。

图14 速率饱和限制大小对有效时间延迟的影响

5.2 瞬态峰值比Δq2/Δq1

瞬态峰值比的计算结果如图15所示。由图可知，a对Δq2/Δq1的影响很小，各构型在不同的a值下都属1级飞行品质。对于构型Ⅰ，a=1(°)/s时，速率饱和限制起作用，Δq2/Δq1增加，此时系统阻尼减小，稳定性变差。

图15 速率饱和大小对瞬态峰值比的影响

5.3 有效上升时间Δt

有效上升时间的计算结果如图16所示。由图可知，a对Δt的影响与a对Δq2/Δq1的影响结果类似，各构型在不同的a值下都处于1级飞行品质边界内。

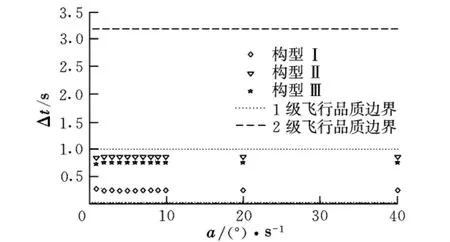
图16 速率饱和对有效上升时间的影响

6 结论

通过本文对比分析计算结果可得到如下结论:

(1)考虑三种非线性环节时，系统的响应延迟均增加，快速性变差;除了死区对系统的稳定性有利以外，间隙和速率限制都将减小系统阻尼，具有使系统不稳定的趋势。

(2)间隙除了使系统延迟增加、快速性变差以外，最主要的影响是在系统中可能引起极限环振荡。随着间隙b的增加，振荡幅值也增加，但振荡的频率没有明显变化。

(3)对于具有不同有效时间延迟t1的线性系统，死区和间隙大小的变化可能引起较大的有效时间延迟，从而导致飞行品质等级发生较大变化。

［1］ 胡寿松.自动控制原理［M］.第五版.北京:科学出版社，2003:684.

［2］ Mitchell D G，Klyde D H.Bandwidth criteria for categoryⅠ and Ⅱ PIOs［R］.NASA Reports，CP-2001-210389，2001:17-19.

［3］ 孟捷，徐浩军，李大伟，等.Gap准则在Ⅱ型PIO预测中的应用［J］.北京航空航天大学学报，2010，36(9):1067-1070.

［4］ 王保国，钱耕.描述函数法及其在非线性人机系统中的应用［J］.人类工效学，2009，15(2):35-39.

［5］ Military Specification.MIL-STD-1797(USAF) Flying qualities of piloting vehicles［S］.USA:Air Force，1997.

［6］ Stevens B L，Lewis F L.Aircraft control and simulation［M］.2nd Edition.USA:John Wiley ＆ Sons Publication，2003:664.