分布式电源接入对配电网电压变化的分析

陈 芳，王 玮，徐丽杰，姜复亮，迟作为，李华顺

（1.北京交通大学电气工程学院，北京100044；2.吉林电力有限公司吉林供电公司，吉林132001）

由于越来越多的分布式能源渗透在配电系统基础设施中，要求未来配电系统具有新的灵活的可重构的网络拓扑、新的保护方案、新的电压控制和新的测量方法[1，2]。如文献[3]研究了多个分布式发电系统的配电网无功优化算法，这对于减少网络功率损耗和提高电压质量有一定的作用。一般认为，分布式发电DG（distributed generation）指为满足终端用户的特殊需求、接在用户侧附近的小型发电系统[4]。文献[5]指出分布式发电可以包含任何安装在用户附近的发电设施。当DG 接入配电网并网运行时，在某些情况下会对配电网产生一定的影响，对需要高可靠性和高电能质量的配电网来说，分布式发电的接入必须慎重[6，7]。

一直以来，DG 接入对配电网电能质量的影响是讨论的热点[8]。DG 接入在给电能质量带来积极影响的同时，也会给电能质量带来消极的影响[9～11]。本文针对一种典型的负荷分布模型，即三角形模型，并且基于电路的叠加定理，对所建模型进行电压分布计算研究，通过分析研究分布式电源出力变化，接入位置变化造成的配电系统电压变化，正确评估分布式电源对配电系统带来的影响，从而使配电系统能够安全、稳定运行。

1 含DG 的配电网负荷分布模型

1.1 分布式发电系统

对于可再生能源分布式发电系统，是一套多电源互相独立的发电系统，它采用直流总线，由发电单元、储能单元、控制单元和模拟负载单元组成，整个系统的结构[12，13]如图1所示。

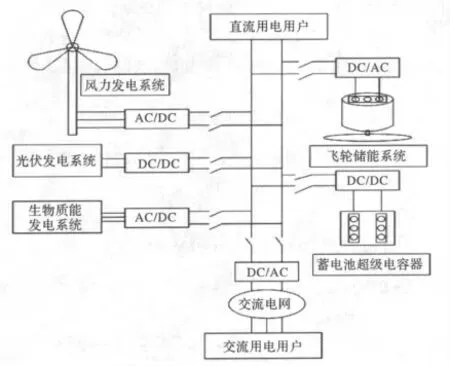
图1 基于可再生能源的分布式发电系统结构图Fig.1 Diagram of distributed generation system based on renewable energy

1.2 含分布式电源的负荷分布模型

配电网的基本单元是馈线，我国馈线电压等级大多是10kV，每条馈线上线路成树状分布，图2为含DG 的简单配电网放射式接线方式。

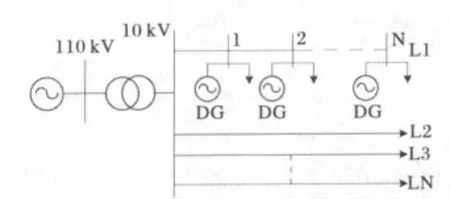
图2 含DG 的简单配电网放射式接线方式Fig.2 Connection mode of simple radial distribution network with DG

为了分析含分布式电源的配电网电压分布情况，采用一种典型的负荷分布模型，即三角形模型，由于负荷均匀分布模型对于线路上负荷分布严重不均匀的情形，会带来较大的误差，而事实上线路上的负荷分布很少是均匀的，故采用三角形模型，以三角形面积表示负荷大小，以此来减小误差，如图3所示。假设馈线长度为m，在k处接入分布式电源，负荷总的有功和无功分别用PL、QL表示，图中三角形的面积表示负荷总的功率，单位长度的电阻、电抗分别用r、x 表示，d 为配电线路中任意一点。

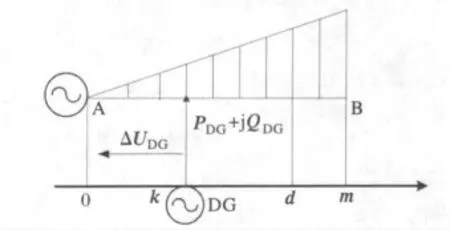
图3 含分布式电源的三角形负荷分布模型Fig.3 Triangle load distribution model with distributed power

当配电线路中只有系统电源单独作用时，d点之前、之后的有功无功负荷分别用P0－d、Q0－d、Pd－m、Qd－m表示，则有：

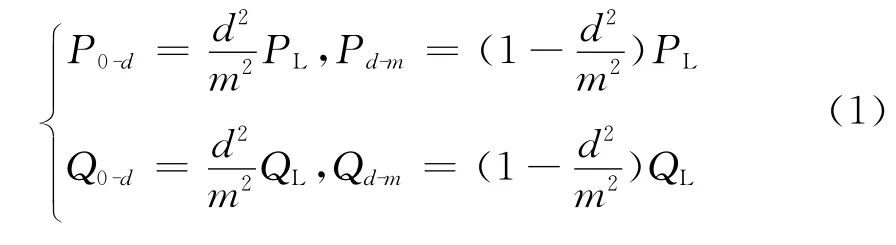
2 电压分布计算

依据图3所建模型，设线路始端A 点电压为U0，线路额定电压为UN，d 为线路任意一点，则d点的电压为

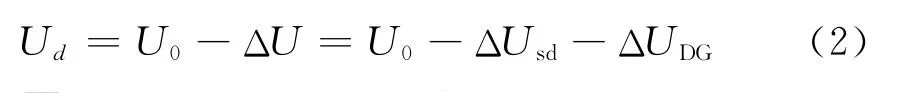
图3所建模型是含分布式电源的简单配电线路，基于电路的叠加定理[14]，分别考虑系统电源和DG 电源对配电线路的作用，所以电压损耗ΔU 包括两部分ΔUsd和ΔUDG，其中ΔUsd是系统电源单独作用引起的，包括两部分内容，ΔUsd1是由于d点之后等效综合负荷引起，ΔUsd2是由于d 点之前以三角形形式分布的负荷引起；ΔUDG是DG 单独作用时引起的。

2.1 系统电源单独作用

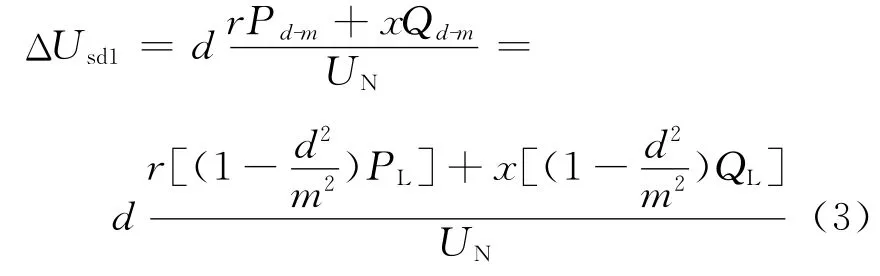
定义负荷密度ρ，且ρ＝Kλ，其中K 为负荷密度系数，K ＝k1＋j k2。从0点到m 处的总负荷为

解方程（4），可得负荷密度系数：

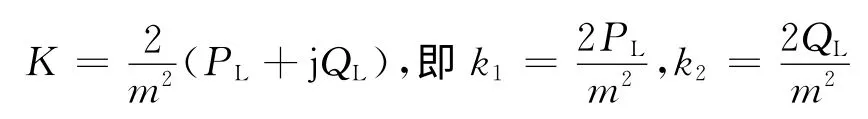
则

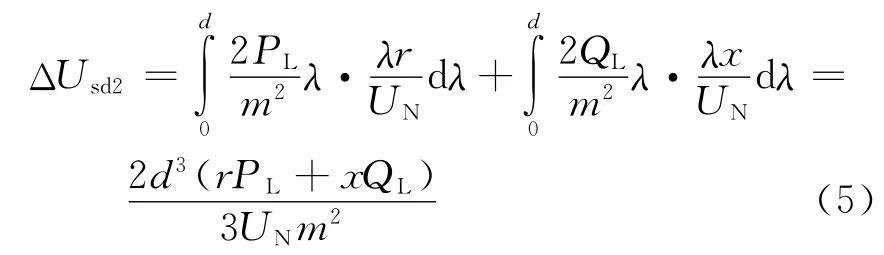
2.2 DG 单独作用

当在k点处接入分布式电源，其容量为PDG＋j QDG，配电线路中只有DG作用时，则d点前后电压损耗分以下两种情况进行讨论：

情况1 0＜d ≤k

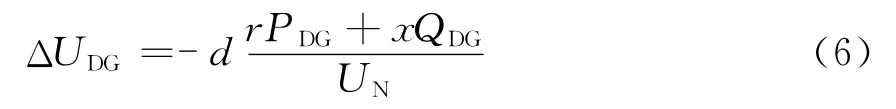
情况2 k＜d ≤m

对于k点之后的线路，DG 对其是没有直接影响的，但是因其对k 点电压的提高，间接影响了k点之后的电压，所以k点之后的电压损耗为

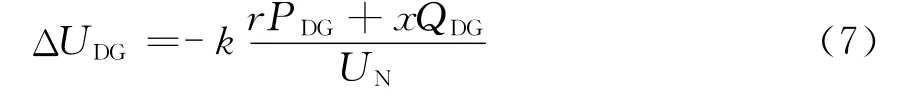
2.3 含DG 的配电网电压损耗

情况1 0＜d ≤k

根据式（2）、（3）、（5）、（6）可得在情况1下d点的电压：

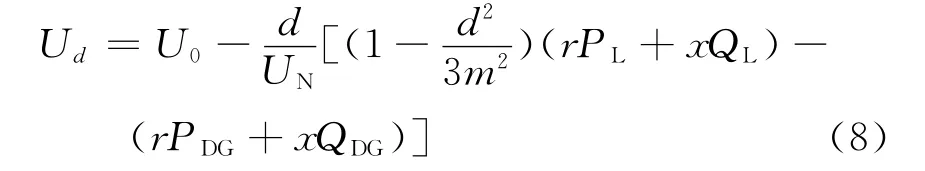
同理，可分析情况2，结果计算如下。

情况2 k＜d ≤m

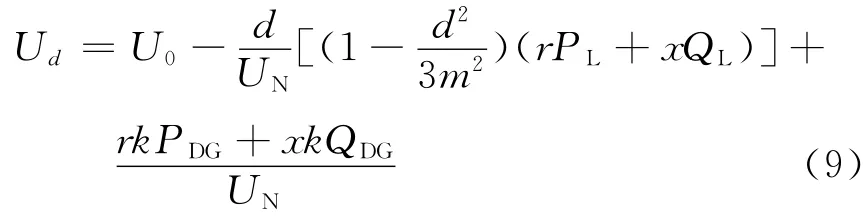
当网络参数，负荷参数给定，DG 容量已知时，d 点的电压便可计算出来。

2.4 负荷成均匀分布的配电网电压损耗

根据以上电压分布计算原理，当负荷均匀分布时，各点电压计算公式如下：

情况1 0＜d ≤k

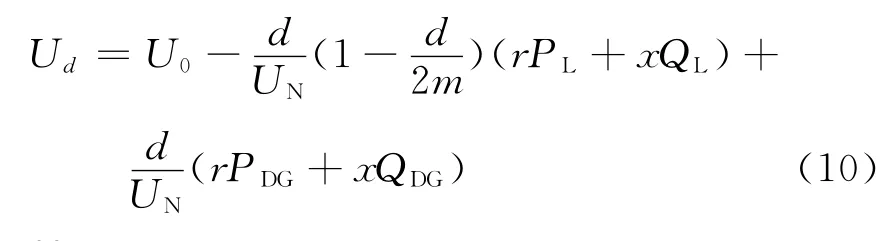
情况2 k＜d ≤m

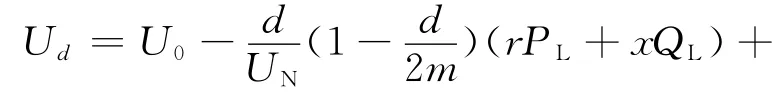
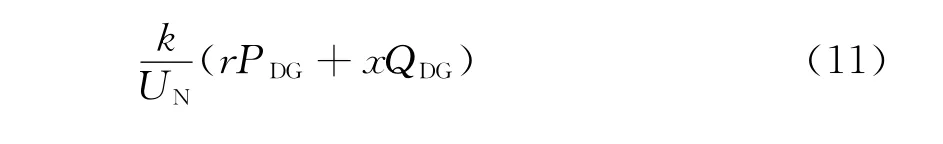
3 算例分析

依照图3所示含DG的配电线路模型，一条10 kV 的配电线路，线路长度为m ＝12km，总负荷数为12，电阻r＝0.082Ω／km，x＝0.247Ω／km，配电线路始端电压Uo＝1.05（标幺值），额定电压UN＝1.0（标幺值），功率基值为10MVA，电压基值为10kV，线路总负荷为：PL＝5 MW，QL＝3 Mvar。DG 有功PDG＝3 MW，功率因数cosφ ＝0.9（滞后）。

算例中各节点负荷数据见表1。

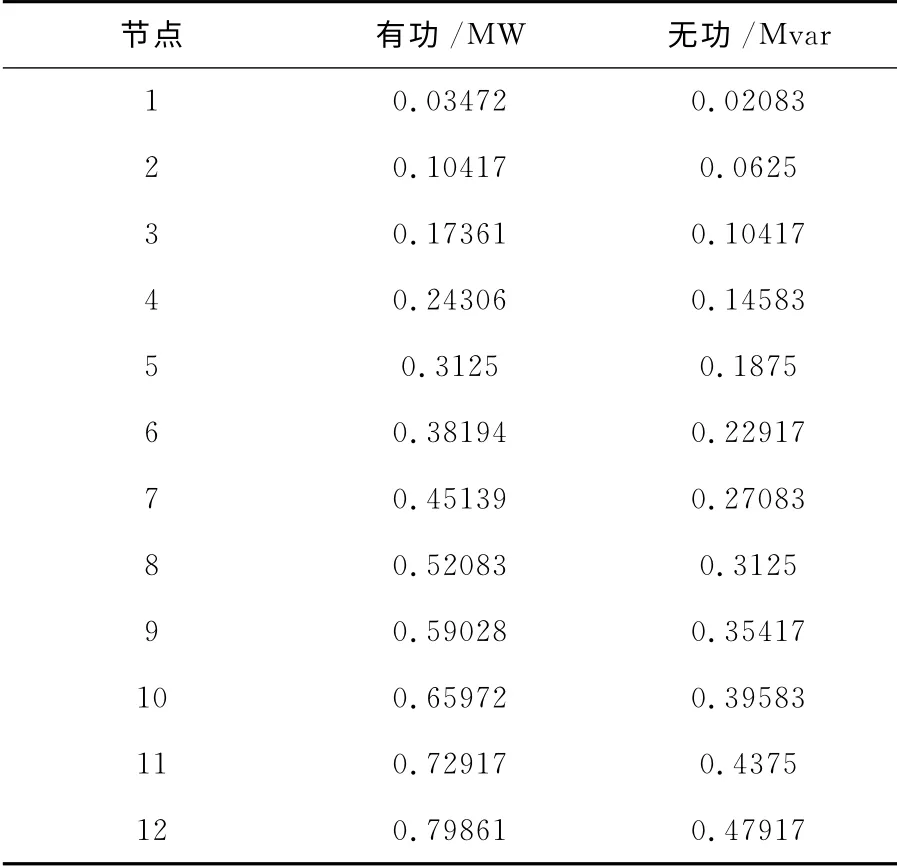
表1 节点负荷数据Tab.1 Loads data

3.1 模型验证

基于以上数据分别对以三角形负荷分布模型和以均匀负荷分布模型的配电网进行电压分布计算，公式分别为（8）、（9）和（10）、（11），将所得计算结果与严格的潮流计算比较来验证方法的正确性和有效性，图4为没有DG 作用的验证图，图5为6号节点接入DG 的验证图。

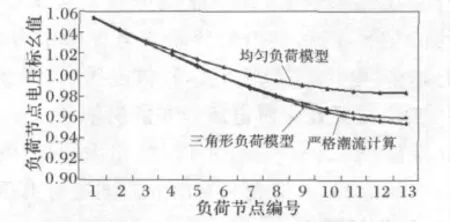
图4 无DG 的模型验证图Fig.4 Model validation without DG

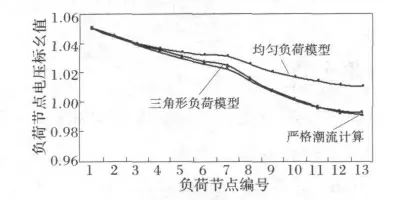
图5 DG 在节点6处的模型验证图Fig.5 Model validation of DG at node 6

通过上图分析可知，基于三角形负荷模型的电压分布计算结果与严格潮流计算结果较为一致，而且要远远优于均匀负荷分布模型的电压分布计算结果，由此验证了三角形负荷分布模型算法在含DG 的配电网电压分析中的正确性和有效性。

3.2 DG 出力变化对电压分布的影响

同样的网络数据和负荷，DG接入6号节点，按照DG出力的0、30%、65%、100%四种方案进行测试，根据文中所给的算法计算电压分布，结果见图6，出力数据见表2。

表2 DG 接入方案及出力数据Tab.2 Access scheme of DG and output data

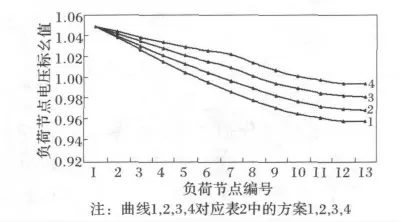
图6 DG 出力变化引起电压分布变化曲线Fig.6 Voltage profiles according to the change of DG output

以上结果表明，在不改变分布式电源接入位置的情况下，电压支撑由分布式电源的出力决定，出力越多，电压支撑就越大，整体电压水平就越高。

3.3 DG 位置变化对电压分布的影响

保持DG出力不变，为100%出力，只改变它在网络中的位置，依据表3给出的方案进行电压分布计算，结果见图7。

从图7可以看出，DG 出力不变，改变接入位置，则电压会有相应的变化，越靠近负荷侧，电压变化幅度就越明显，方案4中电压水平明显高于方案1、2、3的电压水平，方案4中DG 位置靠近负荷侧，方案1中DG 位置靠近母线，可见，DG 的接入位置越靠近线路末端，对电压的影响越大。

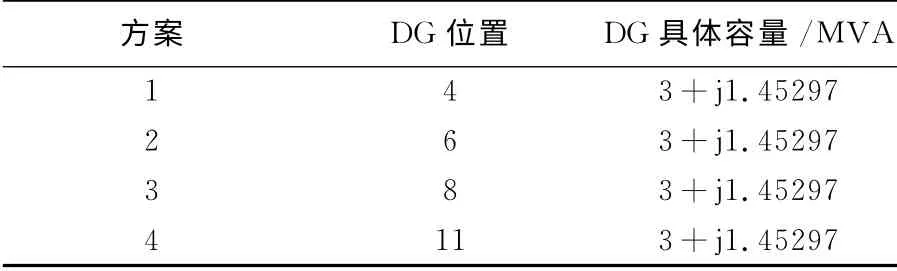
表3 DG 接入方案Tab.3 Access scheme of DG

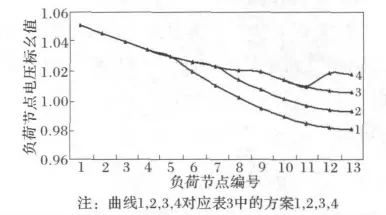
图7 DG 位置变化引起电压分布变化曲线Fig.7 Voltage profiles according to the change of DG interconnecting location

3.4 DG 的电压调节作用

由于分布式发电的发电机具有励磁系统，可在一定程度上调节无功功率，从而具有电压调节能力。实际运行时，当DG 远离变电站时，对变电站母线电压的调节能力就很弱，如图7中方案4就说明了这一点；有些发电机采用感应电机（如风力发电机），可能还要吸收无功，而不适用于电压调节，在这种情况下，就要有相应的无功补偿设备；当大容量的DG 接入时，必须将有关信号和信息传到配电系统调度中心，以进行调度和控制的协调。

4 结论

本文针对链式配电网络，采用含DG 的三角形负荷模型算法进行了电压分布计算，研究结果说明分布式发电对配电网稳态电压分布的影响，并得出如下结论：

1）对配电网进行简化建模和分析的方法中三角形负荷分布模型要优于负荷均匀分布模型，而且文中也验证了三角形负荷分布模型算法的有效性。

2）一定容量的DG接入配电网络，的确会对馈线上的电压分布产生重大影响，影响程度与DG 总容量的大小、接入位置有很大的关系。

3）DG 是否具有电压调节作用与DG 的类型、容量等有关，要根据实际运行状况确定具体的调压方案。

[1]余贻鑫（Yu Yixin）.新形势下的智能配电网（Intelligent distribution network in the new situation）[J].电网与清洁能源（Power System and Clean Energy），2009，25（7）：1－3.

[2]袁超，吴刚，曾祥君，等（Yuan Chao，Wu Gang，Zeng Xiangjun，et al）.分布式发电系统继电保护技术（Protection technology for distributed generation systems）[J].电力系统保护与控制（Power System Protection and Control），2009，37（2）：99－105.

[3]王瑞，林飞，游小杰，等（Wang Rui，Lin Fei，You Xiaojie，et al）.基于遗传算法的分布式发电系统无功优化控制策略研究（Research on the reactive power control of distributed generation system based on genetic algorithm）[J].电 力 系 统 保 护 与 控 制（Power System Protection and Control），2009，37（2）：24－27，52.

[4]Nissen Matthew.High performance development as distributed generation[J].IEEE Potentials，2009，28（6）：25－31.

[5]王敏，丁明（Wang Min，Ding Ming）.含分布式电源的配电系统规划（Distribution network including distributed generation）[J].电力系统及其自动化学报（Proceedings of the CSU－EPSA），2004，16（6）：5－8，23.

[6]刘振亚.智能电网技术[M].北京：中国电力出版社，2010.

[7]冯希科，邰能灵，宋凯（Feng Xike，Tai Nengling，Song Kai）.风力发电机对配电网影响的比较分析（Comparative analysis on the impact of the wind generator connected to the distribution network）[J].电力系统保护与控制（Power System Protection and Control），2009，37（21）：25－30，94.

[8]Driesen J，Belmans R.Distributed generation：challenges and possible solutions[C]∥IEEE Power Engineering Society General Meeting，Montreal，Canada：2006.

[9]Meyer B.Distributed Generation：towards an effective contribution to power system security[C]∥IEEE Power Engineering Society General Meeting，Tampa，USA：2007.

[10]梁才浩，段献忠（Liang Caihao，Duan Xianzhong）.分布式发电及其对电力系统的影响（Distributed generation and its impaction on power system）[J].电力系统自动化（Automation of Electric Power Systems），2001，25（12）：53－56.

[11]王志群，朱守真，周双 喜，等（Wang Zhiqun，Zhu Shouzhen，Zhou Shuangxi，et al）.分布式发电对配电网电压分布的影响（Impacts of distributed generation on distribution system voltage profile）[J].电力系统自动化（Automation of Electric Power Systems），2004，28（16）：56－60.

[12]Ackermann Thomas，Knyazkin Valery.Interaction between distributed generation and the distribution network：operation aspects[C]／／IEEE Power Engineering Society Transmission and Distribution Conference，Yokahama，Japan：2002.

[13]孙云莲.新能源及分布式发电技术[M].北京：中国电力出版社，2009.

[14]邱关源.电路[M].北京：高等教育出版社，1999.