非线性体系动力可靠性分析的等效Duffing体系法

张振浩，杨伟军

（长沙理工大学 土木与建筑学院，长沙410076）

非线性体系的动力可靠性问题具有重要的理论与实用意义。但考虑了结构非线性因素后，结构体系在随机激励下的随机反应求解变得十分复杂，其动力可靠性分析的难度也就更大［1］。在非线性体系的随机振动理论中，等效线性化方法是求解非线性系统随机响应时应用得最广泛的方法并且目前仍在得到不断发展［2－6］。与精确解或数值模拟结果的比较表明，等效线性化方法所给出的二阶矩精度通常是令人满意的，但是，等效线性化方法给出的其它统计量，如相关函数、极值等可能是不可靠的。因此，等效线性化法给出的高安全界限时的超越统计量可能是严重错误的；又如对非线性阻尼系统，用等效线性化得到的首次超越概率与实际值之差可达数个量级［7］。

鉴于上述原因，学者们致力于寻求更好的近似方法。在这当中，等效非线性体系法实质上就曾经被采用过。等效非线性体系法的思想最早是由Caughey提出的［8］，但他提出的方法只适用于原体系是拟线性的情况。朱位秋等［9－10］建立一种适合于求解拟李亚普诺夫系统随机响应的等效非线性系统法。该方法采用的“最佳”等效原则是使等效系统与原系统具有相同的平均能量变化规律（即具有相同的漂移和扩散系数）。笔者采用的等效非线性体系法将保留原体系的刚度非线性特征，而将非线性阻尼等效线性化，即将原非线性体系等效为具有线性阻尼、非线性刚度的结构体系，而这类具有线性阻尼、非线性刚度的非线性体系是可以通过FPK方程法求得其稳态反应过程的精确概率分布的。该方法对原非线性体系无特殊要求，具有普适性。

1 拟Duffing体系的等效非线性分析

1.1 平稳激励下2非线性体系间的等效分析

一般情形下的单自由度非线性体系的振动微分方程可表示为式（1），

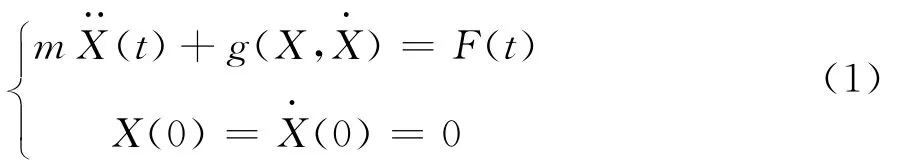
设与方程（1）等价的非线性体系为式（2）所示的Duffing体系，

式中，ce、ke分别为等效阻尼系数与等效刚度系数；ε为常数，当ε＝0时结构退化为线性体系；β（X）为X的奇函数，且有

体系之间的误差可以用方程（1）与（2）之间的差值来表示，以e（t）表示：

误差项e（t）也是一个随机过程。为使等效体系最优地逼近原体系，等效准则采用使等效体系与原体系之间的绝对偏差为最小，对于随机过程，等同于使e（t）的平方的均值（即e（t）的均方值）最小［11］。按此准则来确定等效参数ce与ke。

根据式（3），有

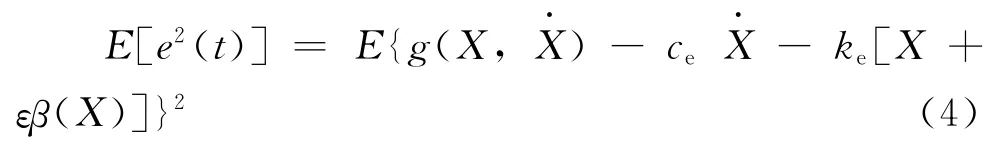
式（4）可以将 E［e2（t）］看作是等效参数ce、ke的二元函数。根据多元函数求极值的方法，可知，要使E［e2（t）］取最小值就相当于要使式（5）成立。

根据式（5），并利用求数学期望与求导运算间的可交换性，最终整理可得式（6）。

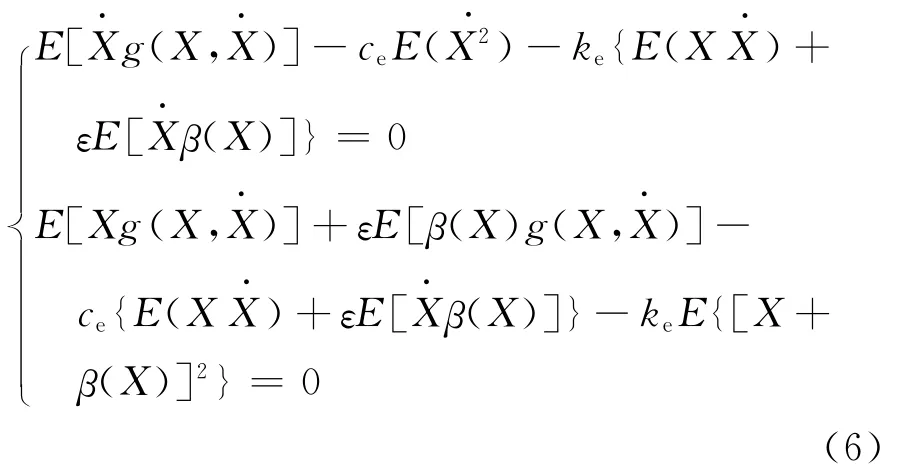
将式（6）联立组成关于ce和ke的方程组，由此求得等效参数ce、ke，见式（7）。

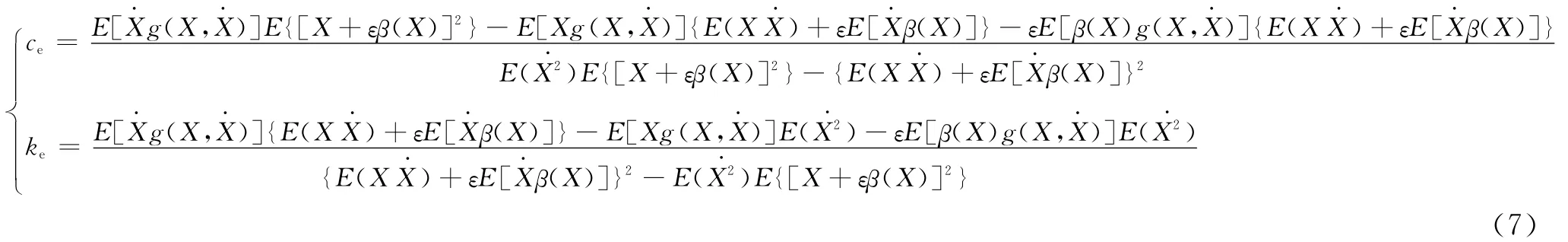
由式（7）可见，要求解等效参数ce、ke，必须知道上式右端的那些数学期望。在不作任何假设的情况下，这些期望值是很难求得的，因为这需要知道反应X（t）和（t）联合概率分布，而这是未知的。

因为激励F（t）为平稳过程，若略去反应过程的过渡阶段，直接考虑稳态下的反应状况，此时根据平稳过程与它的均方导数在同一时刻上总是互不相关的这一结论，可知平稳位移反应X（t）和速度反应（t）互不相关，因此有E［X（t）（t）］＝0。于是，式（7）可简化为式（8）。

在随机等效分析中，通常用等效体系反应的联合概率密度来代替原体系反应的联合概率密度来确定式（7）、（8）或（9）中的数学期望值。由于式（7）、（8）或（9）中的数学期望值是由等效非线性方程（2）得出的，因此这些期望的表达式中将总含有ce和ke。所以，与等效线性化方法类似，等效非线性化方法中，为最终得到ce和ke的具体值，通用的方法是采用迭代法求解：首先假设ce和ke的初值；然后将其代入等效方程（2），由FPK方程法求出反应X（t）和X·（t）的一阶矩、二阶矩以及二阶联合矩；再由式（7）或（8）或（9）求出第一次迭代的ce1和ke1；如此重复以上步骤，直到求得满足收敛准则的ce、ke终值；最后，由ce、ke终值代入等效方程（2），将求得的解作为原非线性体系的近似解。

1.2 非平稳激励情形的讨论

对于非平稳随机激励的情况，由式（7）、（8）或（9）可明显看出，由于ce、ke直接与反应的统计矩有关，而非平稳反应的统计矩是时间t的函数［12］，因此，体系的等效参数是随时间而变化的，即有

此时，等效阻尼和等效刚度以及反应统计矩，就需要从t1＝Δt的离散时刻起按以上步骤迭代计算，直到计算到所需要的时刻tk＝kΔt。

2 结构动力可靠度

通过等效非线性分析将原非线性体系等效为Duffing体系后，可通过FPK方程求得体系的联合概率密度，于是可以方便地采用经典Poisson过程法求得体系的动力可靠度。

Poisson过程法计算基于首次超越破坏机制的动力可靠度基本公式可表示为式（11）［13］，

式中，b1、－b2为双侧安全界限，T 为时段长，（t））为反应过程与安全界限的交差速率，可由赖斯公式计算见式（12），［13］

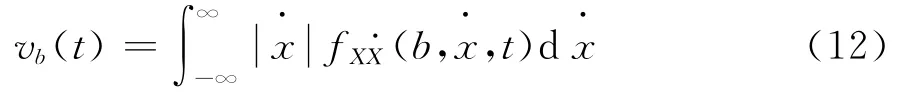
3 算 例

考虑van der Pol振子受高斯白噪声激励，

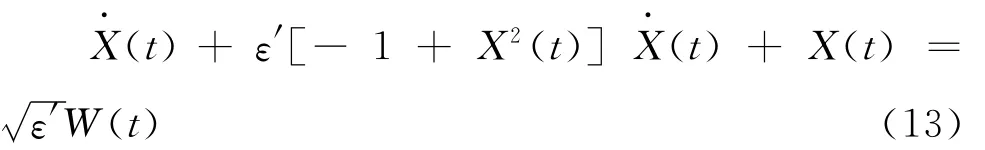
式中，W（t）是谱密度为S0的高斯白噪声，ε′为常参数。试基于首次超越破坏机制分析该非线性体系的动力可靠性。

体系（13）为一复杂非线性体系，首先构造与其等价的非线性体系见式（14），

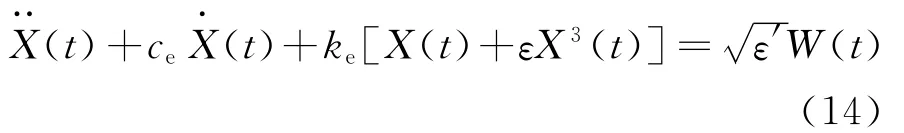
式中ce、ke为根据2体系间的误差最小的准则确定的等效参数。在体系（14）中，它们有明确的物理意义，即ce、ke分别为当ε＝0时Duffing体系退化为线性体系时的阻尼系数和刚度系数。

3.1 等效参数的求解

根据式（9）求出ce、ke的表达式。经比较知：

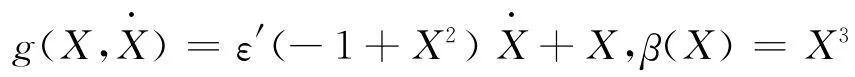
于是，根据数学期望的运算性质，式（9）中的各项期望可求得为

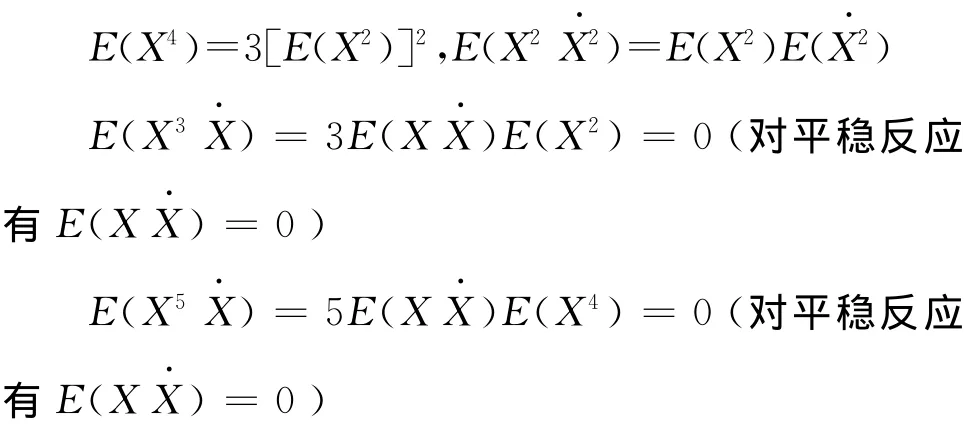
经过化简计算，等效参数ce与ke最终可表示为反应均方值E（X2）的函数见式（15）和式（16）。

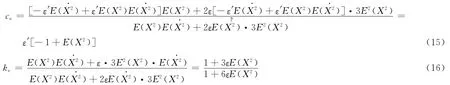
3.2 等效体系的随机反应求解

根据FPK方程法求解等效非线性体系（14），结 果如表1所示。

表1 等效体系（14）的解析解

表中，常数C由归一化条件确定，C＝表示，体系（14）当ε＝0时退化为线性体系时（）（）的位移反应X0t和速度反应t的平稳方差，这2个方差由线性随机振动分析理论可求得，见式（17）。

式（18）即是关于ce和ke的二元方程组，但难以求其解析解，只能通过数值方法求数值解。确定ce和ke值后，再将其反代入表1中的各式即得各项随机反应结果。

3.3 分析结果及讨论

文献［9］给出了van der Pol振子的近似联合概率密度函数，为式（19），

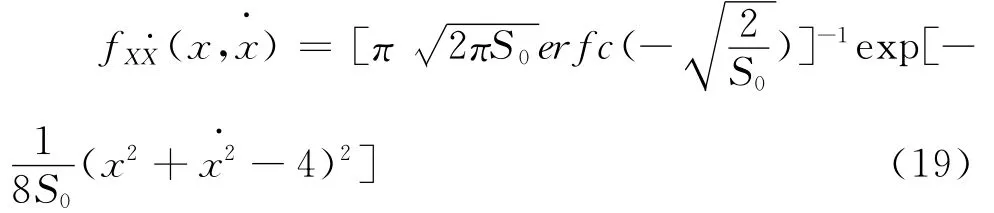
其中erfc（·）为余补误差函数，erfc（x）＝1－erf（x）＝经与数值结果的对比表明，在ε′为小参数时式（19）给出的结果是精度较高的。

以下就将本文的计算结果与式（19）的结果以及等效线性化法分析的结果进行比较。若取参数ε＝0，因为等效非线性体系退化为了线性体系，所以此时可以得到将原非线性体系等效线性化分析的结果。

由表2计算结果对比可以看到，等效非线性法给出的计算结果与文献［9］的结果甚接近，结果是可靠的。此外，与等效线性化分析结果的比较表明，等效非线性分析所给出的结果精度确有提高，而且有随着等效体系非线性参数ε的增大，其计算结果精度也有提高的趋势。因此，等效非线性分析方法是可行的。由表3的计算结果可见，若将原非线性体系等效为线性体系分析其动力可靠性，误差确实比较大，结果与采用 Monte－Carlo数值模拟法［15］的计算结果吻合较好，等效非线性法的计算结果精度明显提高。

表2 随机反应分析结果对比

表3 动力可靠度计算结果对比

4 结 论

非线性体系的动力可靠性分析精度的高低，其关键在于体系的随机反应分析的精度高低。本文提出的基于等效Duffing体系的等效非线性化法，将具有一般普遍性的非线性体系等效为线性阻尼而刚度非线性的这一类可以通过FPK方程求得其精确稳态联合概率密度函数的非线性Duffing体系。算例分析表明，本文方法的计算结果精度较之等效线性化法的精度要好，提高了非线性体系动力可靠性分析结果的精度。此外，由于所采用的等效非线性体系中含有可控制体系非线性强弱的参数ε，因此改变ε值的大小便可容易获得将原非线性体系等效为不同强弱非线性体系时的分析结果；特别的，当取ε为零，便可得到等效线性化的分析结果。这对于问题的研究颇为方便。而ε的最佳取值问题，即ε取多大值时能够获得精度最高的非线性体系可靠度计算结果，这将是需要进一步开展的研究工作。

最后应指出，分析过程中为了简化计算，略去了小参数的高阶项，同时处理高阶反应矩时所采用的正态降阶法也采用了一些近似假设，这些将会对计算结果的精度产生一定影响。

［1］杨伟军，张振浩.基于连续Markov过程首超时间概率分析的结构动力可靠性研究［J］.工程力学，2011，28（7）：124－129.YANG Weijun，ZHANG Zhenhao.Structural dynamic reliability study based on the probability analysis of first－passage time of continuous markov process［J］.Engineering Mechanics，2011，28（7）：124－129.

［2］苏亮，王毅.等效线性化方法中系统参数求解的优化算法［J］.工程力学，2011，28（9）：23－29.SU Liang，WANG Yi.New optimization algorithm for determining system parameters of equivalent linearization method［J］.Engineering Mechanics，2011，28（9）：23－29.

［3］Guyader A C，Iwan D.Determining equivalent linear parameters for use in a capacity spectrum method of analysis［J］.Journal of Structural Engineering，2006，132（1）：59－67.

［4］Lin Y Y，Miranda E.Noniterative equivalent linear method for evaluation of existing structures ［J］.Journal of Structural Engineering，2008，134（11）：1685－1695.

［5］陈衍茂，刘济科.一种改进的等效线性化方法［J］.应用力学学报，2008，25（2）：296－298.CHEN Yanmao，LIU Jike.Improved equivalent linearization method［J］.Chinese Journal of Applied Mechanics，2008，25（2）：296－298.

［6］王伟，刘必灯，周正华，等.刚度和阻尼频率相关的等效线性化方法［J］.岩土力学，2010，31（12）：3928－3933.WANG Wei，LIU Bideng，ZHOU Zhenghua，et al.Equivalent linear method considering frequency dependent stiffness and damping ［J］.Rock and Soil Mechanics，2010，31（12）：3928－3933.

［7］ZHU W Q，HUANG Z L，SUZUKI Y.Equivalent nonlinear system method for stochastically excited and dissipated partially integrable Hamiltonian systems［J］.International Journal of Non－Linear Mechanics，2001，36（5）：773－786.

［8］Caughey T K.On the response of nonlinear oscillators to stochastic excitation.American Society of Mechanical Engineerings，Applied Meehanics Division，1984，65：9－14.

［9］朱位秋，余金寿.预测非线性系统随机响应的等效非线性系统法［J］.固体力学学报，1989，10（1）：34－44.ZHU Weiqiu，YU Jinshou.Equivalent nonlinear system method for predicting response of nonlinear systems to random excitations［J］.Acta Mechanica Solida Sinica，1989，10（1）：34－44.

［10］朱位秋.非线性随机动力学与控制［M］.北京：科学出版社，2003.

［11］张振浩.结构动力可靠性理论研究及RC梁桥抗震可靠性分析［D］.长沙：长沙理工大学，2010.

［12］杨伟军，张振浩，林立.基于破坏指标界限值的结构抗震可靠度分析［J］.地震工程与工程振动，2010，30（1）：77－83.YANG Weijun，ZHANG Zhenhao，LIN Li.Research on seismic reliability of structure based on boundary value of damage index［J］.Journal of Earthquake Engineering and Engineering Vibration，2010，30（1）：77－83.

［13］Ang A H S，Tang W H.Probability concepts in engineering—emphasis on applications to civil and environmental engineering ［M］.John Wiley ＆ Sons Ltd，2007.

［14］李杰，陈建兵.随机振动理论与应用新进展［M］.上海：同济大学出版社，2009.

［15］刘佩，姚谦峰.采用重要抽样法的结构动力可靠度计算［J］.计算力学学报，2009，26（6）：851－855.LIU Pei，YAO Qianfeng.Dynamic reliability calculation based on importance sampling method［J］.Chinese Journal of Computational Mechanics，2009，29（6）：851－855.