数学科学在流域水环境监测中的应用研究
刘 巍,栾卫中,孟庆华
(1.松辽流域水资源保护局,吉林 长春 130021;2.大唐长春第二热电有限责任公司,吉林 长春 130021;3.松辽水利委员会综合服务中心,吉林 长春 130021)
数学科学在流域水环境监测中的应用研究
刘 巍1,栾卫中2,孟庆华3
(1.松辽流域水资源保护局,吉林 长春 130021;2.大唐长春第二热电有限责任公司,吉林 长春 130021;3.松辽水利委员会综合服务中心,吉林 长春 130021)
本文选择了数学科学有关门类,如:线性代数、集合论、概率论、模糊数学等,与监测科学进行跨学科地交叉研究,从理论与实践的结合上证明,数学就是监测学的方法论基础。在应用技术方面有创新,对流域水环境监测而言,价值巨大,意义深远。
数学科学;水环境;监测;应用研究
数学涉及一切事物,关联所有领域,特别是水环境监测学中,如果没有数学科学的应用,就没有质量,没有价值。因为水环境监测本身就是用量化的概念去研究、掌握环境质量现状、变化规律及发展趋势,所以,数学科学就是它的方法论基础。大量科技文献证明:有下列一些数学科学门类,在水环境监测学中必不可少,非用不可。当然是选择运用。
1 线性代数
在水环境监测中的点位设计、质量评价、预测预报及监测管理中,有很多问题归结到求解一个线性方程的问题,常用的数学知识有:“行列式”、“向量”与“向量空间的概念”、“矩阵”概念等等。
1.1 行列式及其性质
线性方程组求解时,往往要用到“行列式”这个数学工具。其要求是:
1)对于给定的2个二元线性方程所构成的线性方程组:
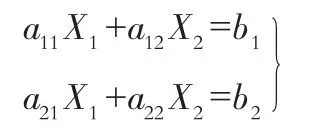
经消元法及“交差相乘相减”处理后,可得二行二列式,即:

2)对于含有n个n元线性方程的方程组,即:
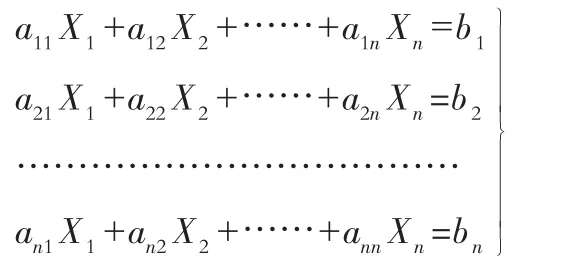

3)行列式有如下性质:
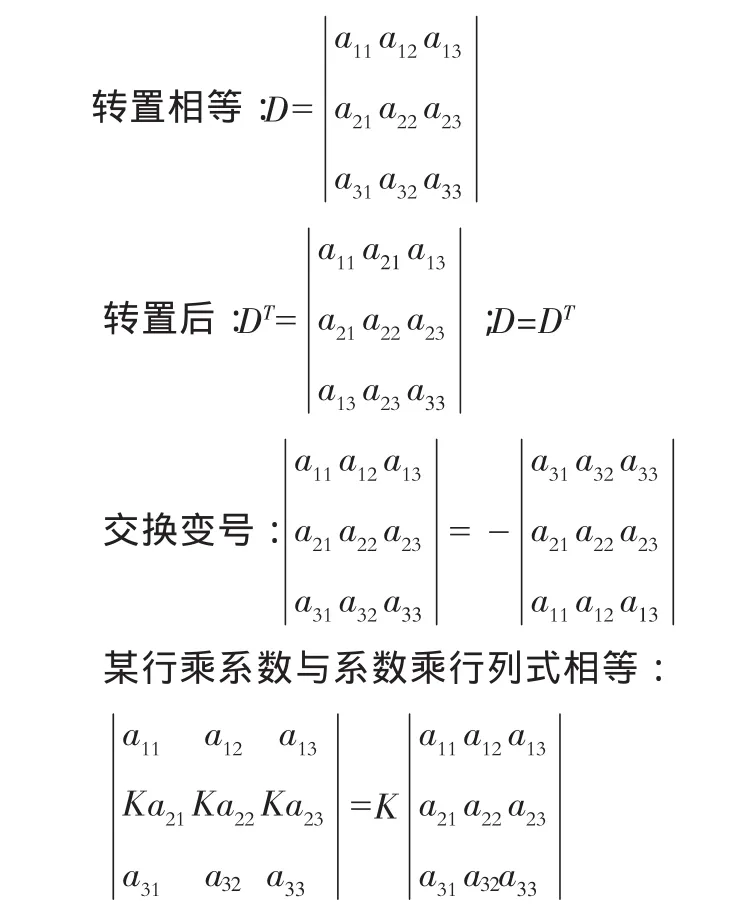
某一行的各元素是二项之和,则可将行列式改成两个行列式之和:
任一行(或列)中各元素与其代数余子式的乘积的和等于行列式的值,任一行(或列)的元素与另一行(或列)的对应元素的代数余子式乘积的和等于0:

1.2 向量概念
在解析几何中关于向量概念的基础,根据水环境监测问题的需要,及其他重要的环境问题一样,往往需要用更多的“量”来刻画同一现象或问题,而超过三维空间就无法给予几何描述,为此,定义:把n个数写成一个有序的数组(a1,a2,…,am),则称此数组为 n 维空间的一个 n 维向量,并用a表示。

向量组的线性相关性判断是:
1)如果向量组a1,a2,…,an中有一部分与向量线性相关,则全组也线性相关。
2)如果向量组 a1,a2,…,an线性无关,则其中任一部分向量也线性无关。
3)如果在 m(m>1)个向量 a1,a2,…,am中有一个是零向量,则这m个向量线性相关。
1.3 矩阵概念
矩阵概念在水环境监测的布点、数据分析、质量评价中用的很多,尤其是聚类分析,是一个有力的工具。矩阵的定义为:由m×n个数按一定次序排列的有m行n列的表,即:

称为矩阵,其中aij为矩阵的元素。
矩阵的运算要点是:
1)加法:若矩阵A的行数分列数分别与矩阵B相同,即:

2)乘数:设有

3)乘法:只有矩阵A的列数等于矩阵B的列数时,才有矩阵的乘法。设有:

4)交换律:A+B=B+A
5)结合律:A+(B+C)=(A+B)+C
2 集合论
集合(集)是近代数学最基本的概念,凡具有某一同性质的可以互相区别的事物的全体被当作一个整体来考虑时,就是一个集合。如,自然环境质量和社会环境质量构成的集合就是整体环境质量;如水体、空气、固体废弃物、生物等环境要素的环境质量所构成的集合就是自然环境质量;化学污染、物理污染、生物污染所构成的集合就是环境污染……构成集合的事物叫做集合元素,给定一个集合时,必须说清元素的特征,即给出判别的准则。元素和集合的表示方法常用的是A={0,1,2,…,m},表示集合A是0和前m个自然数所组成,其有m+1个元素;B={1,2,3,…,m}表示B是由自然数组成的集合。一般称A为有限集合,B为无限集合,集合的初等运算性质有:幂等律,A∪A=A,A∩A=A;排中律,A∩A=φ;交换律,A∪B=B∪A,A∩B=B∩A;结合律,A∪(B∪C)=(A∪B)∪C,A∩(B∩C)=(A∩B)∩C;分配律,A∪(B∪C)=(A∪B)∩(A∩C),A∩(B∪C)=(A∩B)∪(A∩C);吸收律,A∪(A∩B)=A,A∩(A∪B)=A;空集性质,A∩φ,A∪φ=A。
3 概率论
概率论是数理统计学——数学科学的重要分支学科的基础,关于概率论的基本理论,在水环境监测中用得十分普遍。如果说统计学是从样本到总体的“推理学”,那么,概率论就是从总体到样本的“推理学”。在通常的水环境监测中要具备的概率论知识有:
3.1 排列与组合概念
在n个不同元素中任选r个(不许重复,r≤n)按一定顺序排成一列,称为选排列,其排列总数为:
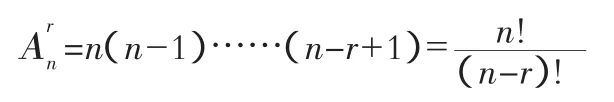
另有全排列、可重复的排列、同物排列等,分别表示为:
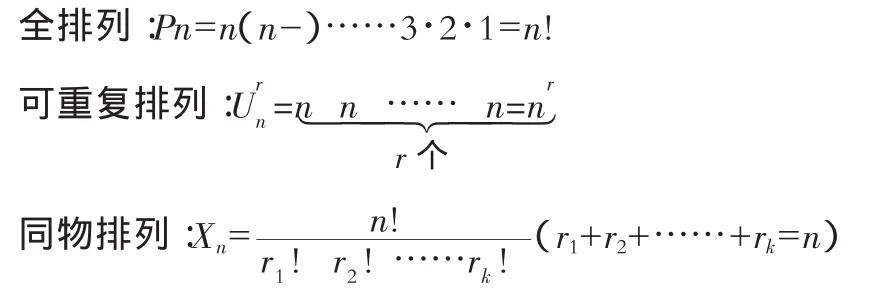
从n个不同元素中任取r个(不许重复,r≤n)不计顺序构成一组,称为从n个不同元素中取r个的一个组合,组合数为:

3.2 随机试验和随机事件概念
概率论中的这一概念与集合论中的集合有许多相似之处,随机试验的全体基本事件组成的集合即为“基本事件空间”,随机事件可称为该空间的一个子集,随机事件之间的关系及事件的运算和集合论中的子集相同,并、交、差、补等基本相似。若事件A发生必然导致B发生,则称事件A包含于事件B,记为A⊂B或B⊃A;若B⊃A且A⊂B,则为A事件与B事件相等,记为A=B;同理,和、积、差分别记为:A+B(或 A∪B)、AB(或 A∩B)、A-B;互不相容事件记为A∩B=φ;对应事件记为B=A。
3.3 概率的定义
若随机事件A在n次试验中出现K次,则称K为事件A在n次试验中出现的频率,记为fn(A)=,若随机试验的基本事件空间仅含有限个基本事件,而且基本事件出现的可能性相等,则称为古典型试验。A的概率为:P(A)=。
3.4 随机变量与分布函数概念
定义:如果每次试验的结果可以用一个ξ来表示,而且对任何实数X,“ξ<X”有着确定的概率,则称ξ是随机变量,依试验结果的不同性质,又可分为离散型随机变量与连续型随机变量。
1)离散型随机变量最重要的分布规律有。

卜阿松分布:ξ-P(λ)。
2)连续随机变量的主要分布。
均匀分布:

3.5 随机变量的数学特征

4 模糊数学
模糊数学是用数学方法研究和处理具有“模糊性”现象的数学。在水环境监测中,常常要用模糊数学方法进行聚类分析(即模糊聚类),其要点是:
1)设U是需要被分类的对象全体(集合),即因素集。R为相似矩阵,R的元素rij应满足:0≤rij≤1。
设被分类的对象Uj由一组数据Xi1,Xi2,……,Xim来表示。ri1表示Ui和U1的相似程度构成相似矩阵R。
2)聚类。能够进行聚类分析的模糊矩阵R必须是等价矩阵。即需同时满足自反性、对称性和传递性。所以,需采用传递闭包的方法对矩阵R进行改造。
模糊矩阵相乘表示了两个模糊关系合成,有:

当R2n=Rn时,矩阵Rn则具有传递性并满足等价关系,其中,模糊矩阵的乘法与普通矩阵乘法相比较,运算过程一样,对具有等价关系的矩阵R采用取入截集的方法将模糊矩阵变为普通逻辑矩阵,进行聚类。当入取值从1降到0时,分类由细变粗,逐步归并,形成一个动态的聚类图。
5 数学模型在水环境监测中的应用
所谓数学模型系指使用数学符号、函数和关系式等,抽象地表示其有关主题、程序或系统。
水环境数学模型以仿真、副近客观实际为目标,以地面水环境为重点,以完善的理论和方法,突出实际应用为特点。这里必须强调的是:
1)在地表水体模型中,全面、系统地建立水库、湖泊中有机污染物和富营养化物质总磷、三氮、重金属三态(溶解态、悬浮态、底泥态)迁移转化模型,考虑到分子扩散、系统扩散,底泥、水温和生物对浓度的影响,建立了总磷迁移转化的三维水动力——水质——生态——水温耦合模型;还建立了地表水——地下水联合水质模型。
2)在地下水模型中吸收了国内外最新研究成果,加强了海水入侵,热迁移及非饱和带的污染物质迁移问题。
3)随着水环境问题的日益增多,在解决这些问题中,全面、系统、深入定量化地进行水资源和水质模拟、预测、管理研究成为关注焦点。水环境数学模型在近20~30年内已经发展成为一门重要的学科,在科研、生产、工程等领域均起到重要的指导作用,还被应用于水污染治理与规划之中。
X832
A
1002-0624(2012)06-0025-04
2012-03-16

