有限元法在吉林省中部城市引松供水工程中的应用
王 倩,侯 薇,鞠 晔
(1.吉林省水利水电勘测设计研究院,吉林 长春 130000;2.水利部松辽水利委员会,吉林 长春 130021)
有限元法在吉林省中部城市引松供水工程中的应用
王 倩1,侯 薇1,鞠 晔2
(1.吉林省水利水电勘测设计研究院,吉林 长春 130000;2.水利部松辽水利委员会,吉林 长春 130021)
有限元法具有考虑岩土介质的非均匀性、各项异性、非连续性和材料与几何非线性,且能适应于各种实际边界条件的优点,在隧洞分析中比常规计算方法具有一定的优越性。本文针对吉林省中部城市引松供水工程中的有压隧洞,采用有限元法计算在不同围岩类别条件下开挖隧洞所引起的位移变形、应力和应变值,分析围岩稳定性,为设计、开挖及维护隧洞提供可行性方法。
有限元;有压隧洞;围岩稳定性;引松供水工程
1 概 述
吉林省中部城市引松供水工程初步拟定从第二松花江流域丰满水库坝上左岸取水,途经温德河、岔路河、饮马河、双阳河到达丛家岭分水枢纽,分别由长春干线、辽源干线、四平干线及各附属支线供水给长春市、四平市、辽源市及所属的九台市、德惠市、农安县、公主岭市、梨树县、伊通县、东辽县、长春双阳区等11个市、县、区的城区,以及供水线路附近可直接供水的25个镇。
工程总体布局由1条总干线、1处分水枢纽、3条干线、干线3个调节水库、13条支线、支线7个调节水库和各线路上相应交叉及附属建筑物组成。输水线路总长550.6 km,其中输水总干线起点为丰满水库左岸,终点为冯家岭分水枢纽,全长110 km,有压隧洞长91 km,占总干线长度的83%。
因此,如何合理、科学、精确地进行隧洞结构计算成为中部城市引松供水工程项目的关键问题之一。
2 有限元技术
2.1 方 法
隧洞属于地下修筑的结构物。由于对地下结构的特性认识不充分,在设计方法上多数是沿用地面结构的设计方法,但是这种方法与实际情况相差很大。随着科学技术的提高,人们对地下结构的认识有了进一步的深入,已经认识到地下结构是由周边围岩和支护结构两者共同组成,并相互作用的结构体系,即地下结构=支护结构+周边围岩。
隧洞的动静力学计算是一项比较困难的课题,地层岩土介质和隧洞结构相互作用相当复杂。只有那些具有规则几何形状和理想的材料特性,且荷载形式与边界条件是简单的线弹性体系,才能得到较为精确的解答。但是,对于非线性岩土体内的连续或不连续介质和任意几何外形的隧洞结构,其力学计算必须借助于近似的数值方法:有限元法、边界元法、有限元—边界元耦合法。
对于隧洞,主要关心的区域是隧洞附近,可用有限元法。有限元法的优点在于可以考虑岩土介质的非均匀性、各项异性、非连续性和材料与几何非线性,且能适用于各种实际的边界条件;缺点在于要求分析区域的几何、物理连续性[1]。
2.2 采用的强度理论
非线性有限元方法分析隧洞在开挖过程中的变形、应力及应变,考虑了岩石本身的非线性本构关系,能够模拟施工过程,可适用于任意复杂的边界条件,但由于岩石本身的复杂性,导致采用不同的屈服准则对有限元计算结果有很大影响。
经典强度理论是针对无摩擦的金属材料建立起来的,而且假设抗拉强度等于抗压强度,故该理论对于岩石这种具有摩擦且拉压强度相差悬殊的材料并不适用[2]。
目前岩土材料常采用莫尔-库仑屈服准则(M-C)和广义米赛斯屈服准则。莫尔-库仑屈服准则较好地反映了岩土材料拉压不等的特性,应用最为广泛,但也存在诸多缺点,例如,它在三维应力空间中的屈服面存在棱角奇异点而导致数值计算不收敛。为此前人对其做了大量的修正,总体上看,这些修正准则将在π平面上的六角形屈服曲线抹圆,虽较好地解决了莫尔-库仑屈服准则棱角不收敛的问题,但表达式往往过于复杂,不便于应用。与莫尔-库仑屈服准则及其众多的修正准则不同,广义米赛斯屈服准则在π平面上是一个圆,且表达式简单,便于数值计算。广义米赛斯准则的一种德鲁克-普拉格准则可由莫尔-库仑准则基于关联流动法则推出,在π平面上是莫尔-库仑准则的内切圆。
以平面应变理想弹塑性为条件,并且基于非相关联流动法则,也可以将莫尔-库仑屈服准则转化为具有相同的数学表达形式的广义米赛斯屈服准则,推导过程省略。说明平面应变条件下莫尔-库仑匹配的广义米赛斯屈服准则在关联流动法则和非关联流动法则条件下都与莫尔-库仑屈服准则形式一致。
采用德鲁克-普拉格准则(D-P准则)既可以考虑中间主应力和静水压力对剪切屈服或强度的影响,也克服了莫尔-库仑屈服准则(M-C)存在棱角奇异点而导致数值计算不收敛的缺点。可见,D-P准则作为有限元分析的强度理论是科学、合理的。
3 计算实例
吉林省中部引松供水工程主体工程91 km隧洞,底坡为1/6 000,设计引水流量38 m3/s,开挖直径7 m。隧洞施工采用以TBM施工为主,钻爆法施工为辅的联合施工方法。前段61.8 km采用3台掘进机施工,每台控制在18~20 km。
3.1 计算模型
该工程隧洞大部分属于长距离深埋隧洞,在对隧洞进行开挖过程的有限元模拟分析中,为了使模型更加接近实际,计算模型采用边界尺寸是洞径的7~8倍,岩体单元采用PLANE42来模拟,衬砌单元采用BEAM3来模拟,共9 527个单元。
考虑到隧洞施工过程的最不利情况,计算中采用全断面开挖施工方法,对不加任何支护手段的裸洞进行围岩稳定性分析,通过对洞室周边围岩的应力场、位移场以及塑性区的对比分析,从而揭示开挖隧洞周边围岩的应力应变规律,进而为隧洞进行合理支护设计做参考。
3.2 模型参数
根据隧洞围岩的物理力学性质,在此次有限元计算当中,采用了弹塑性的非线性有限元法。围岩材料的本构模型采用 Drucker-Prager(D-P)模型,以计算隧洞结构与地层在开挖过程中发生的非线性变形特性。采用的各类围岩参数依据钻爆施工方法确定,如表1所示。
3.3 计算成果及分析
以Ⅳ类围岩的隧洞有限元分析为例,洞室开挖后的等效应力、水平位移及竖向位移见图1~3,计算结果列于表2。
计算结果表明,隧洞开挖后Ⅱ,Ⅲ类围岩拱顶变形很小,仅有1 mm左右,由于此次计算选取的Ⅳ类围岩参数比较保守,隧洞开挖后围岩拱顶变形不到5 mm,Ⅴ类围岩则几乎达到25 mm,随着围岩岩性力学性能的下降,等效应力值逐渐减小,而等效塑性应变值逐渐增大,到Ⅴ类围岩达到11.56%,可见Ⅱ,Ⅲ类围岩基本可以达到自稳,Ⅳ类围岩顶拱两侧部位等效塑性应变达4.45%,说明Ⅳ,Ⅴ类围岩均开始出现塑性变形,应重点对这些部位加强支护,以防发生崩塌事故。

表1 各类围岩物理力学参数

图1 Ⅳ类围岩洞室开挖后等效应力图

图2 Ⅳ类围岩洞室开挖后水平位移图
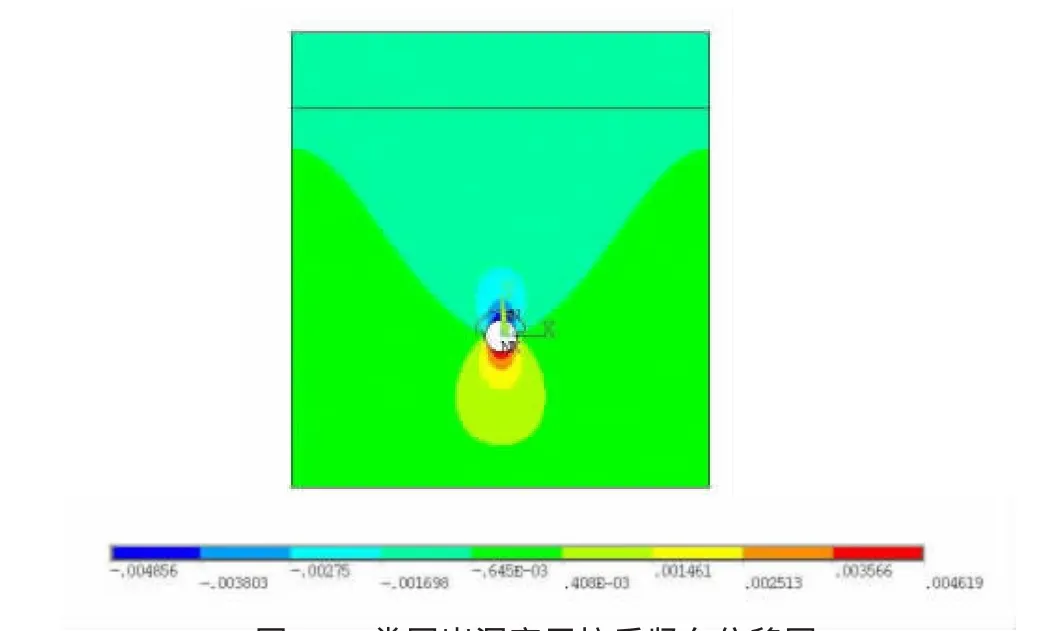
图3 Ⅳ类围岩洞室开挖后竖向位移图
4 结语
由于目前吉林省中部引松供水工程仍然处于可研阶段,关于隧洞有限元分析也处于初探状态,隧洞有限元分析还存在几个问题:1)目前有限元模型参数依据钻爆法施工的经验值,缺乏试验性数据及掘进机施工监测数据;2)对于过河及浅埋地段的Ⅴ类围岩采用无粘结预应力衬砌有待进一步进行有限元计算;3)处于高埋深且节理发育段Ⅴ类围岩的处理方式要进一步采用有限元方法模拟。

表2 各类围岩计算结果
[1]郝文化.ANSYS土木工程应用实例[M].北京:中国水利水电出版社,2005.
[2]薛守义.高等土力学[M].北京:中国建材工业出版社,2007.
Application of FEM in water diversion project from Songhua river to middle cities of Jilin province
WANG Qian,HOU Wei,JU Ye
The FEM has advantages of considering heterogeneity,anisotropy,discontinuity,material nonlinearity and geometric nonlinearity of rock and soil media,adapts to various actual boundary conditions,and is superior to routine method in tunnel analysis.According to the pressure tunnel of water diversion project from Songhua river to middle cities of Jilin province,the paper calculates displacement deformation,stress and strain value caused by tunnel excavation for different class of surrounding rock with FEM,analyzes the surrounding rock stability,and provides creditable data for design,excavation and maintenance of tunnel.
finite element;pressure tunnel;surrounding rock stability;water diversion project from Songhua river
TV67
B
1002-0624(2012)06-0005-03
2011-09-22

