仿鲨鱼鳃部射流减阻特性的仿真研究

谷云庆，赵刚，赵华琳，郑金兴，王飞，肖磊，刘文博

(1.哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨150001;2.大庆油田责任有限公司矿区服务事业部，黑龙江大庆163000)

0 引言

有关减阻技术的研究从20 世纪70年代开始逐渐深入，降低阻力对节约能源的重要意义已经得到各国学者的充分肯定。在交通运输、军事、体育等诸多领域，都迫切需要研究有效的减阻方法来降低阻力。在现有的减阻方法中，仿生减阻方法模拟生物进化获得的某些减阻特征，得到了很好的减阻效果，具有广阔的应用前景。如利用与鲨鱼鳞片具有相似结构的沟槽表面减阻［1-3］，使用与海豚表皮相似弹性特征的柔性表面减阻［4-7］，利用仿照昆虫表面设计的非光滑表面减阻［8］等都是仿生研究的重要成果。

鲨鱼是具有快速运动能力的水生动物，观察发现其身侧前部排列着宽大的鳃板，其功能除与呼吸密切相关外，还可能与降低自身运动阻力有着密切关系。基于仿生研究的基本原理，本文通过对鲨鱼鳃的形态特征进行简化，在平板表面构建了与鲨鱼鳃部射流特征类似的射流出口，采用计算流体力学软件ANSYS CFX 研究仿鲨鱼鳃部射流的减阻特性并分析减阻机理。

1 模型建立及数值计算方法

1.1 仿鲨鱼鳃部射流表面模型的建立

如图1所示为鲨鱼鳃部特征图。为方便、有效地研究鲨鱼鳃部射流这一特征对阻力的影响，对鲨鱼鳃部特征进行了简化，用布置在平板上游的两个条形射流出口构建仿鲨鱼鳃部射流模型，如图2所示。其尺寸参数为:平板厚1 mm、长20 mm、宽6 mm，条形射流出口距流场入口边缘2 mm，条形出口宽度a=0.5 mm，长度b=2 mm.为评价仿鲨鱼鳃部射流模型的减阻效果，需将其所受总阻力与光滑表面进行对比，如图3为对照光滑表面模型，平板厚1 mm，长20 mm，宽6 mm.

1.2 控制方程

在流场求解时所用连续方程、动量方程和能量方程可以写成以下通用形式:

图1 鲨鱼鳃部特征图Fig.1 Feature of shark gills

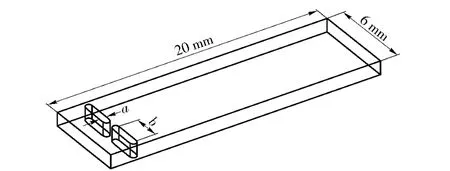
图2 带有射流出口的表面模型Fig.2 Model of surface with jet outlet

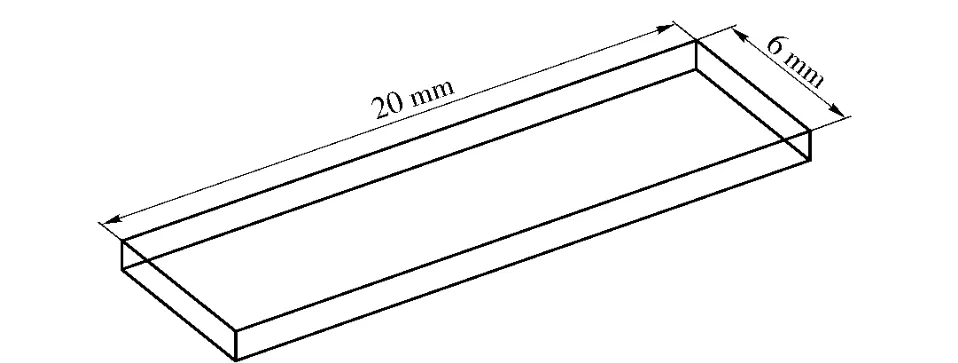
图3 对照光滑表面Fig.3 Comparative smooth surface

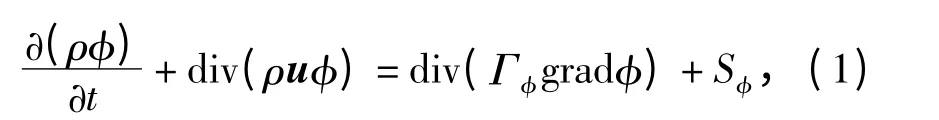
式中:φ 为通用因变量;Sφ为广义源项;u 为速度矢量;Γφ为广义扩散系数;ρ 为流体密度;t 为时间。表达各类方程时各参数的具体形式如表1所示，表中μ 为动力粘度系数，ui为各速度分量。

表1 表达各类方程时各符号的具体形式Tab.1 Concrete terms of symbols in different equations

1.3 湍流模型

因为SST 湍流模型采用建立混合函数的方法，使湍流模型方程在壁面附近流场到远离壁面的流场之间实现平稳过渡，避免了在近壁区域使用壁面函数法带来的问题，提高了仿真的精度［9-10］。所以，针对近壁区流体对壁面的阻力特性研究，选用SST湍流模型具有很好的仿真效果。该模型所用湍流动能方程为

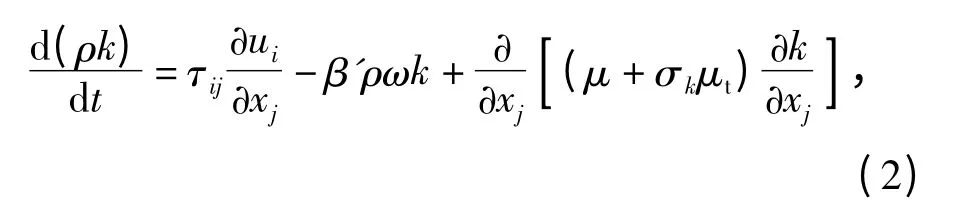
湍流频率方程为

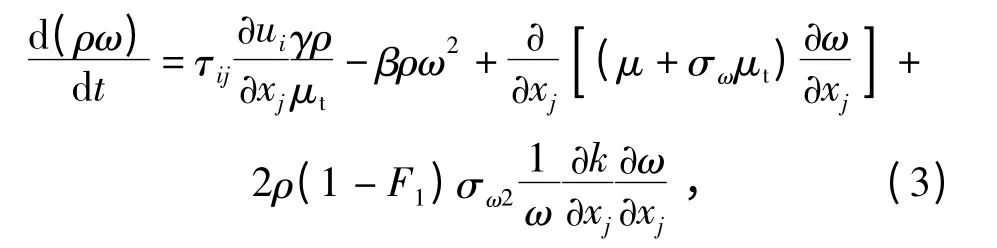
式中:

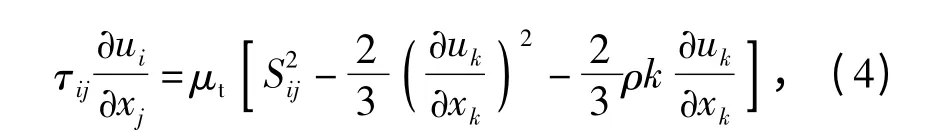
其中Sij为应变张量。

构建SST 湍流模型需要将k-ω 湍流模型和kε 湍流模型混合，φ 为SST 湍流模型中的常数，则

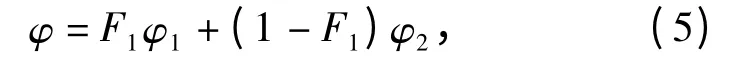
式中φ1、φ2分别为k-ω 湍流模型和k-ε 湍流模型中的常数。混合函数F1、F2分别为

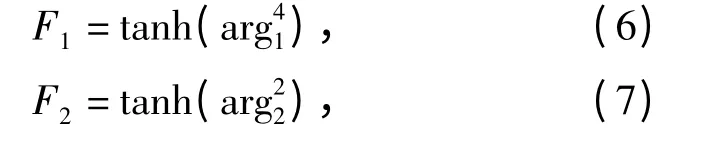
式中:

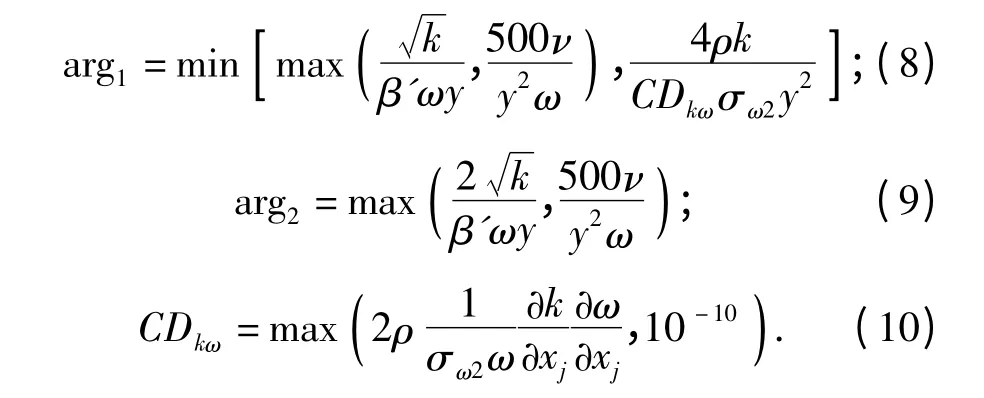
湍流黏性系数为

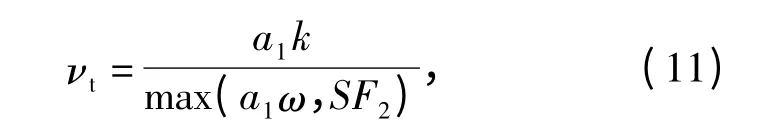
湍流模型中各相关参数详见文献［11 -12］.

1.4 计算域、边界条件与网格划分

为有效利用计算资源并达到理想的计算精度，取距模型表面6 mm 的流场空间作为计算域，其具体尺寸X∶Y∶Z 为20 mm∶6 mm∶6 mm，如图4所示。

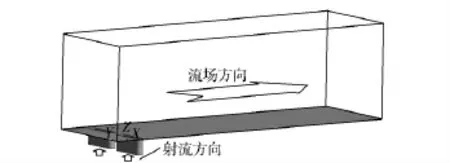
图4 计算域示意图Fig.4 Sketch of computational domain

边界条件为:上壁面为滑移壁面，下壁面及射流出口壁面为无滑移壁面，两侧为对称壁面，射流入口速度ue取值分别为:0.02 m/s、0.04 m/s、0.06 m/s、0.08 m/s、0.1 m/s、0.12 m/s、0.14 m/s、0.2 m/s、0.3 m/s、0.4 m/s、0.5 m/s、0.6 m/s、0.7 m/s、0.8 m/s、0.9 m/s、1 m/s.计算域入口平均速度ua为3 m/s，湍流强度为5%，出口压力为0.

由于SST 湍流模型在近壁区利用低雷诺数法处理壁面流场，因此为保证计算精度，采用混合网格离散流场。在远离壁面的流场区域划分四面体网格，最大网格尺寸0.3 mm;为捕捉边界层流场特性，在壁面附近增加了细密且均匀增长的棱柱型网格，棱柱型网格层数n =20，其中第一层网格节点到壁面的距离Δy 约为0.006 mm，其计算式如下:

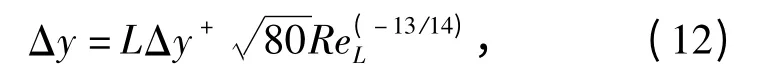
式中:L 为流场长度;Δy+为第一层网格节点到壁面的无量纲距离，对于壁面附近的低雷诺数流场，取Δy+=1;ReL为基于流场长度的雷诺数，其计算式为

式中:u∞为来流速度;ν 为流体的运动粘度，取值为1.006 ×10-6m2/s.网格如图5所示。

图5 边界层处的面网格Fig.5 Surface meshes in boundary layer

2 仿真结果及分析

2.1 仿鲨鱼鳃部射流对表面摩擦阻力的影响

图6所示为不同射流速度条件下仿鲨鱼鳃部射流模型的摩擦阻力对比图。其中摩擦阻力计算式为

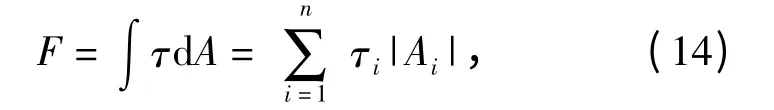
式中:τ 为壁面剪应力;A 为壁面面积;τi为壁面离散单元剪应力;Ai为壁面离散单元面积。

由图6可知，当射流速度小于0.3 m/s 时，模型所受摩擦阻力随速度增大而减小，当射流速度大于0.3 m/s 时，摩擦阻力随射流速度增大成近线性关系增大。

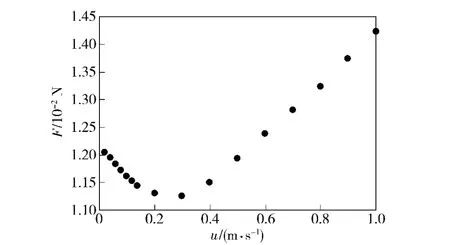
图6 不同射流速度时的摩擦阻力对比图Fig.6 Contrast diagram of frictional resistances at different jet velocities

2.2 仿鲨鱼鳃部射流对压差阻力的影响

如图7所示为不同射流速度条件下仿鲨鱼鳃部射流模型的压差阻力对比图。压差阻力计算式为

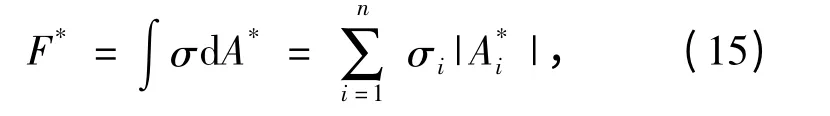
式中:σ 为模型壁面所受压应力;A*为射流出口壁面在沿主流场流动方向的投影面积;σi为壁面离散单元压应力;A*i为壁面离散单元沿主流场流动方向的投影面积。

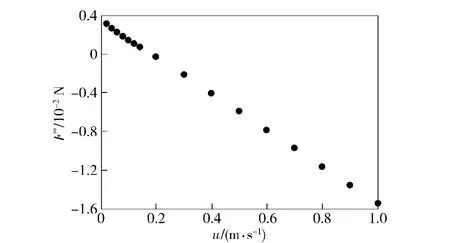
图7 不同射流速度时的压差阻力对比图Fig.7 Contrast diagram of pressure drags at different jet velocities

图7表明，压差阻力与射流速度呈近线性关系，且随射流速度增大逐渐减小。

2.3 仿鲨鱼鳃部射流对总阻力的影响

仿鲨鱼鳃部射流模型总阻力包括表面摩擦阻力和压差阻力两部分，即

将仿鲨鱼鳃部射流模型总阻力与光滑平板总阻力进行对比，对仿鲨鱼鳃部射流模型的减阻效果进行评价。减阻率

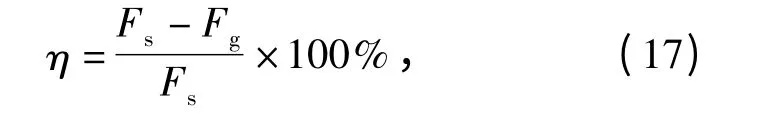
式中:Fs为光滑表面总阻力，通过对其流场进行数值模拟，得到结果为0.013 422 1 N;Fg为仿鲨鱼鳃部射流模型总阻力。

如图8所示为不同射流速度时的减阻率对比图。当射流速度小于0.1 m/s 时表现为增阻，当射流速度大于0.1 m/s 时具有减阻效果并且减阻率随射流速度增加呈近线性关系增大。以上分析表明，当射流速度大于0.1 m/s 时仿鲨鱼鳃部射流具有较好的减阻特性。

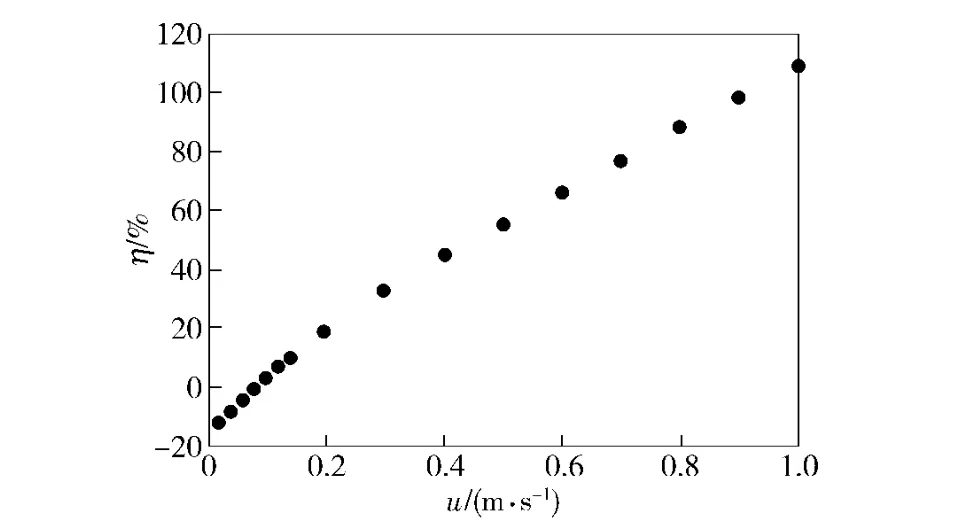
图8 不同射流速度时的减阻率对比图Fig.8 Contrast diagram of drag reduction rates at different jet velocities

3 减阻机理分析

根据对摩擦阻力、压差阻力和减阻率变化规律的研究，当射流速度为0.02 m/s、0.3 m/s 和1 m/s时，阻力分量与减阻率出现极值，下面对这3 种条件下的流场参数进行分析，研究仿鲨鱼鳃部射流的减阻机理。

如图9所示为射流速度分别为0.02 m/s、0.3 m/s、1 m/s 条件下，仿鲨鱼鳃部射流模型与对照模型的壁面剪应力对比图。由图可知，与对照模型壁面剪应力相比，仿鲨鱼鳃部射流可以明显减小射流出口下游区域所受剪应力，且当射流速度增大时，仿鲨鱼鳃部射流对下游的影响范围增大，剪应力降低的区域逐渐向下游延伸;另一方面，受仿鲨鱼鳃部射流影响，相邻射流出口间的壁面剪应力有所增大，且随着射流出口速度的增加，壁面剪应力增大的区域也向下游发展。在不同射流速度条件下，上述变化直接导致仿鲨鱼鳃部模型壁面剪应力的分布差异，从而影响了模型受到的摩擦阻力。

图9 不同射流速度时壁面剪应力对比图Fig.9 Contrast diagram of wall shear strengths at different jet velocities

如图10 所示为射流速度u 分别为0.02 m/s、0.3 m/s、1 m/s 条件下，仿鲨鱼鳃部射流模型与对照模型流场截面(截面位置为x =3 mm)的速度分布图。由图可知，与对照模型相比，仿鲨鱼鳃部射流向出口下游近壁处注入低速流体，使近壁处低速流场厚度增加，即边界层黏性底层增厚、速度梯度降低，该变化减小了壁面所受剪应力，从而降低了摩擦阻力;当射流速度增大时，近壁处低速流场厚度增大，进一步减小了模型壁面受到的摩擦阻力，对减阻起促进作用。

如图11～图12 所示为射流速度u 分别在0.3 m/s和1 m/s 条件下，仿鲨鱼鳃部射流模型流场截面(剖面位置为y =1.5 mm)的速度矢量分布图。由图可知，当射流速度大于0.3 m/s 时，出口下游近壁处出现反向旋涡。当射流速度增大时，旋涡结构的尺寸增大，其结构如图13 所示。稳定的旋涡结构使边界层流体运动有序化，降低了湍流脉动对壁面的作用，仿鲨鱼鳃部射流对流场的这种影响同样减小了模型的摩擦阻力。

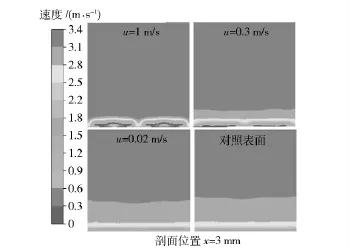
图10 x=3 mm 处流场截面的速度分布图Fig.10 Velocity distribution at the flowfield profile at x=3 mm

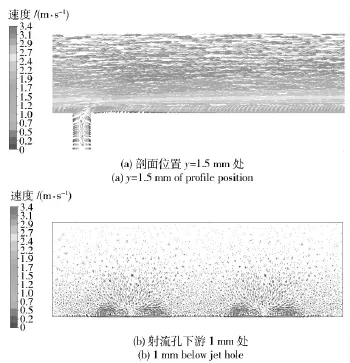
图11 u=0.3 m/s 时流场截面的速度矢量图Fig.11 Velocity vector map of flow field profile at u=0.3 m/s

如图14 所示为射流速度u 分别为0.02 m/s、0.3 m/s、1 m/s 条件下射流出口壁面靠近上游和靠近下游壁面的压力对比图。由图可知，受不同速度仿鲨鱼鳃部射流的影响，靠近下游的出口壁面压力pd和靠近上游的出口壁面压力pu存在差异，其分析结果如表2所示。由于仿鲨鱼鳃部射流模型差阻力F*主要受射流出口壁面压力影响，因此pd和pu的变化直接导致了仿鲨鱼鳃部射流模型压差阻力的变化。

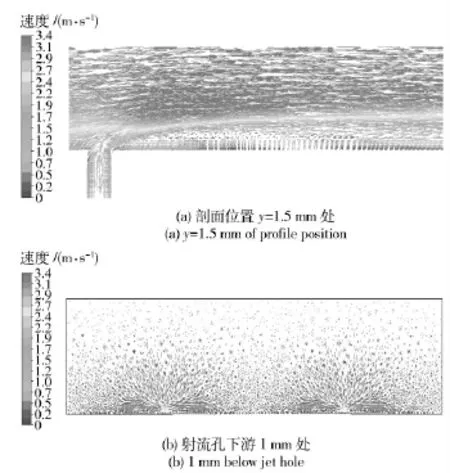
图12 u=1 m/s 时流场截面的速度矢量图Fig.12 Velocity vector map of flow field profile at u=1 m/s

图13 射流出口下游旋涡结构示意图Fig.13 Sketch of the eddy structure below jet outlet's

图14 不同射流速度时射流出口壁面的压力对比图Fig.14 Contrast diagram of pressures on the walls of jet outlet at different jet velocities

表2 压差阻力变化及机理分析Tab.2 Change of pressure drag and mechanism analysis

对图11～图13 旋涡结构的分析可知，旋涡的发展导致射流出口下游附近产生反向流，反向流对仿鲨鱼鳃部射流产生逆流向的推动作用，从而导致靠近下游射流出口壁面的压力pd减小且pd＜pu，使模型的压差阻力下降。

4 结论

本文在流场入口平均速度为3 m/s 条件下，对不同射流速度仿鲨鱼鳃部射流模型的减阻特性进行了仿真研究，并分析了减阻机理，得到以下结论:

1)仿鲨鱼鳃部射流能够改变模型表面所受摩擦阻力。当射流速度在0.02～0.3 m/s 时，表面摩擦阻力减小;当射流速度大于0.3 m/s 时，表面摩擦阻力增大。其减阻机理为:仿鲨鱼鳃部射流使出口下游流场的黏性底层增厚，边界层流体的速度梯度降低、壁面剪应力减小。另外，射流出口下游存在反向旋涡，稳定的大涡结构使边界层流体运动有序化，降低了湍流脉动对壁面的作用。

2)仿鲨鱼鳃部射流模型的压差阻力与射流速度间存在近线性关系，当射流速度增大时，压差阻力减小。压差阻力降低的机理为射流出口下游旋涡导致近壁处出现反向流，反向流对仿鲨鱼鳃部射流产生逆流向的推动作用，使靠近下游射流出口壁面所受压力为负，导致了模型压差阻力的下降。

3)仿鲨鱼鳃部射流可以明显降低总阻力，且射流速度对仿鲨鱼鳃部射流的减阻效果有着重要影响。当射流速度小于0.1 m/s 时表现为增阻;当射流速度大于0.1 m/s 时表现为减阻，但其减阻机理不同，射流速度为0.1～0.3 m/s 时是因为模型壁面剪应力的降低，射流速度大于0.3 m/s 时是因为模型压差阻力的降低。

References)

［1］ Wang J J，Lan S L，Chen G.Experimental study on the turhulent boundary layer flow over riblets surface［J］.Fluid Dynamics Research，2000，27(4):217 -229.

［2］ Viswanath P R.Aircraft viscous drag reduction using riblets［J］.Progress in Aerospace Sciences，2002，38(6):571 -600.

［3］ Han M，Lim H C，Jang Y G ，et al.Fabrication of a micro-riblet film and drag reduction effects on curved objects［C］∥The 12th International Conference on Solid - State Sensors，Actuators and Microsystems.Boston:IEEE Electron Devices Society，2003:396-399.

［4］ Huang J C，Johnson M W.Boundary layer receptivity measurements on compliant surfaces［J］.International Journal of Heat and Fluid Flow，2008，29(2):495 -503.

［5］ Pavlov V V.Dolphin skin as a natural anisotropic compliant wall［J］.Bioinspiration ＆ Biomimetics，2006，1(2):31 -40.

［6］ Fish F E.The myth and reality of Gray's paradox:implication of dolphin drag reduction for technology ［J］.Bioinspration ＆ Biominetics，2006，1(2):17 -25.

［7］ Zheng Z C.Effects of flexible walls on radiated sound from a turbulent boundary layer［J］.Fluids and Structures，2003，18(1):93 -101.

［8］ Tian L M，Ren L Q，Liu Q P，et al.The mechanism of drag reduction around bodies of revolution using bionic non-smooth surfaces［J］.Journal of Bionic Engineering，2007，4(2):109 -116.

［9］ Catalano P，Amato M.An evaluation of RANS turbulence modeling for aerodynamic applications ［J］.Aerospace Science and Technology，2003，7(7):493 -509.

［10］ Grove D V，Wang Z J.Computational fluid dynamics study of turbulence modeling for an ogive using cobalt flow solver and a 2N tree-based cartesian grid generator［C］∥43rd AIAA Aerospace Sciences Meeting ＆ Exhibit.Reston.US:American Institute of Aeronautics and Astronautics，2005，1042:1 -10.

［11］ Menter F R.Two-equation eddy-viscosity models for engineering applications［J］.AIAA Journal，1994，32(8):1598 -1605.

［12］ 张成春，任露泉，王晶，等.旋成体仿生凹坑表面流场控制减阻仿真分析［J］.兵工学报，2009，30(8):1066 -1072.ZHANG Cheng-chun，REN Lu-quan，WANG Jing，et al.Simulation on flow control for drag reduction of revolution body using bionic dimpled surface［J］.Acta Armamentarii，2009，30(8):1066 -1072.(in Chinese)