捷联惯导系统两种速度更新算法的比较研究

林玉荣，陈亮，付振宪

(哈尔滨工业大学 航天学院，黑龙江 哈尔滨150001)

0 引言

传统捷联惯性导航算法［1-2］，通过将变换到导航系下的比力进行积分获得速度增量，积分过程中进行了截断与简化，导致算法精度降低。

对偶四元数能够将转动和平移统一表征［3-7］，文献［8］利用其设计了对偶四元数捷联惯性导航算法，准确求解出了速度增量，并指出“对高动态、大机动状态下的高精度导航来说，对偶四元数算法是更好的选择”。文献［9 -11］通过仿真测试进一步验证了对偶四元数在精度上的优势，但并未分析造成两种算法精度差别的原因。

针对传统速度更新算法与对偶四元数速度更新算法，本文从理论上研究了二者的不同之处，并通过定义两类误差，对二者之间的精度差别作出了定性的表征，同时也给出了定量的分析，结论的正确性通过高动态环境下的仿真测试得到了验证。

1 两种速度更新算法

设速度更新周期ΔT =tm-tm-1，为了便于理论分析，设导航周期等于速度更新周期，并选惯性坐标系I 为导航坐标系。考虑到引力加速度和哥式加速度大小和方向在速度更新周期内变化缓慢，由此引起的不可交换性误差很小，因此下面对两种速度更新算法进行理论分析时不考虑引力加速度和哥式加速度，只讨论载体本身运动对速度计算的影响。

1.1 传统速度更新算法

在忽略引力加速度和哥式加速度的情况下，载体相对地球的运动速度在惯性导航坐标系上的投影为

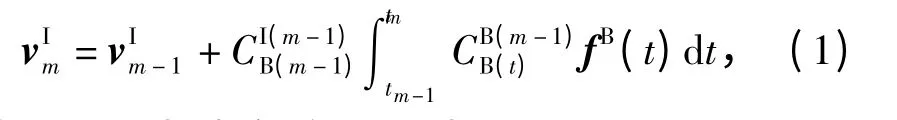
(1)式积分项为速度增量，记为

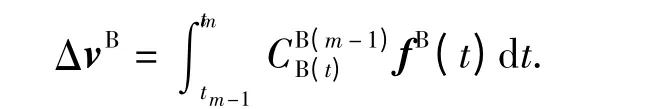
根据旋转矢量与姿态矩阵的关系，速度增量的准确表达式可写为

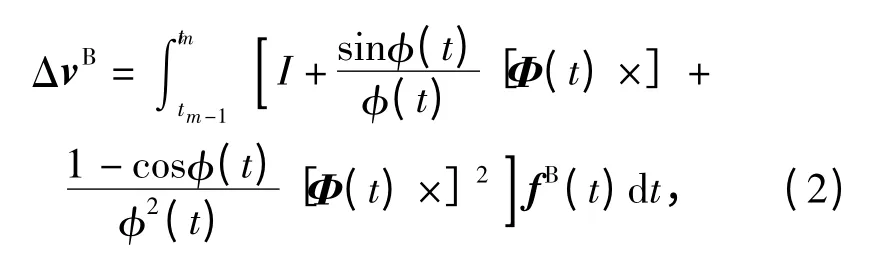
式中:Φ(t)为B(m -1)坐标系至B(t)坐标系的等效旋转矢量;φ(t)= |Φ(t)|.(2)式准确求解非常困难，考虑到ΔT 较小，有如下近似:

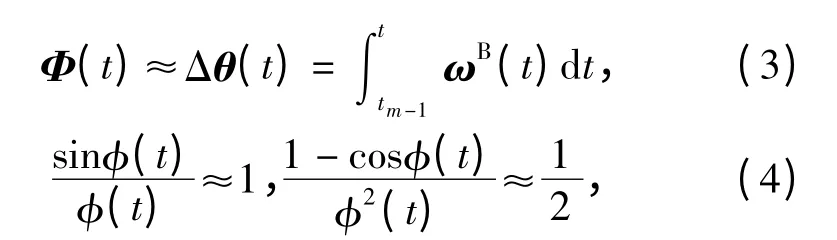
将(3)式与(4)式代入(2)式，并忽略二阶小量［Φ(t)×］2，得到传统导航算法的速度增量表达式

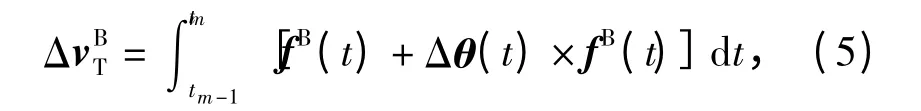
实际导航解算中，导航计算机利用陀螺的角增量输出与加速度计的速度增量输出求解(5)式，计算公式如下:

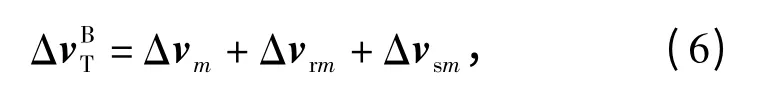
1.2 对偶四元数速度更新算法

刚体在空间中从I 到B 的运动，如图1所示，可分解为:先绕过点c 的单位向量l 旋转θ 角，后沿l的方向平移距离d(或者先沿l 的方向平移距离d，后旋转θ 角).上述的旋转和平移运动可以用对偶四元数统一描述为

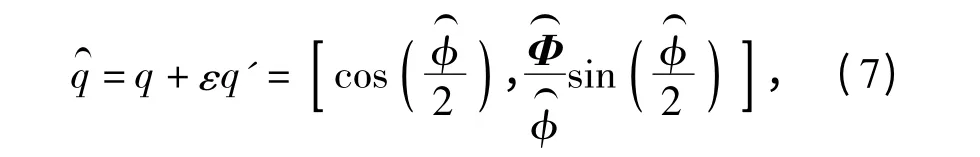
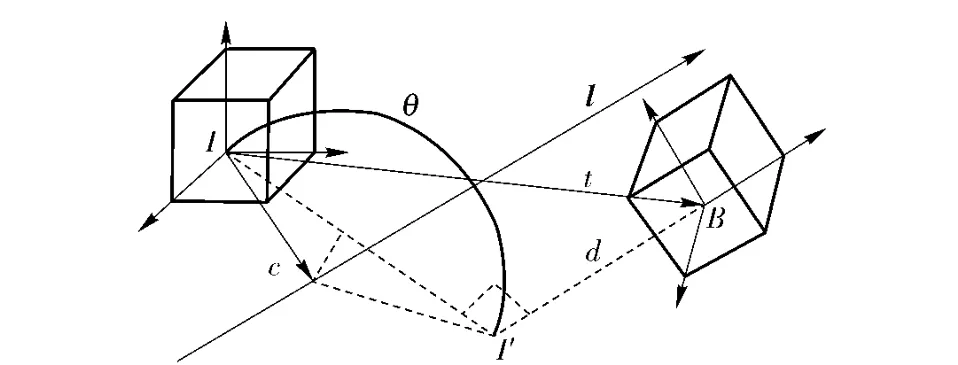
图1 旋转和平移的几何表示Fig.1 Geometric representationof rotation and translation

与传统的速度更新算法不同，在对偶四元数导航算法中可直接获得定义在惯性导航系中的地速(载体相对地球的速度)增量的精确解［2］。若将一个速度更新周期内载体系(B 系)相对于惯性系(I系)运动的对偶四元数记为

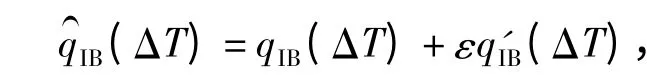
则地速增量的精确解为

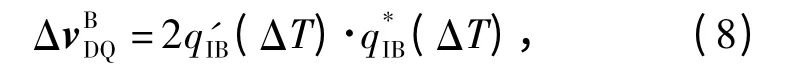
式中q*IB(ΔT)为qIB(ΔT)的共轭。

根据(7)式和(8)式有

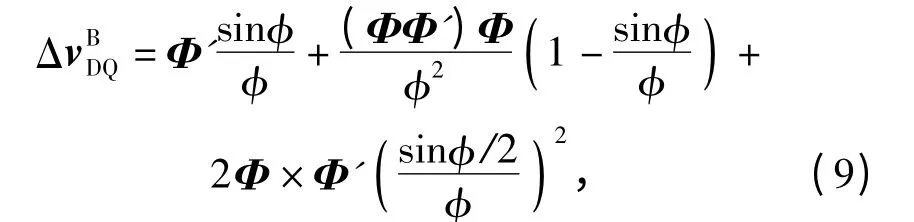
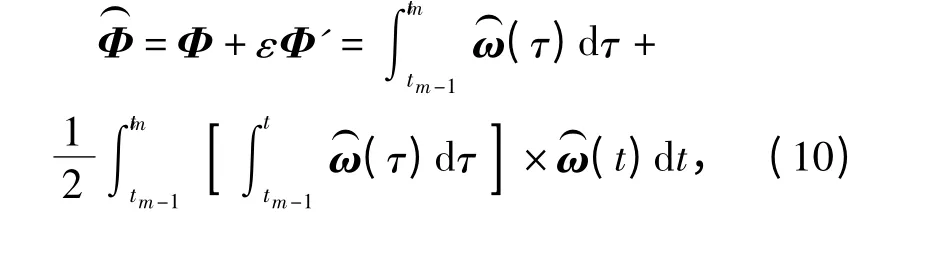
且

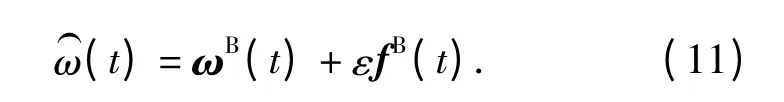
应用二重向量差乘变换公式

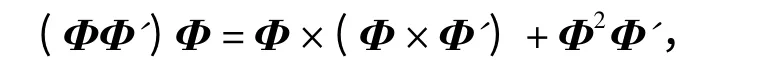
(9)式可化为

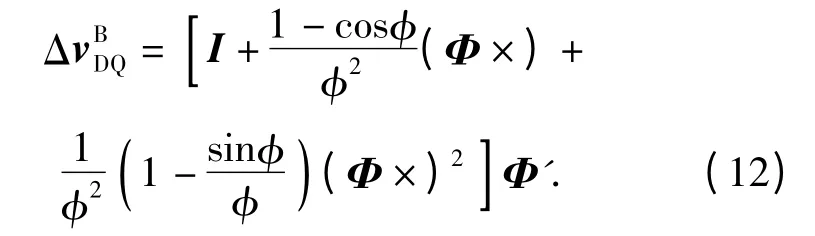
对(12)式中的三角函数取4 阶近似，忽略高阶小量，可得到对偶四元数速度更新算法中的速度增量计算公式如下:

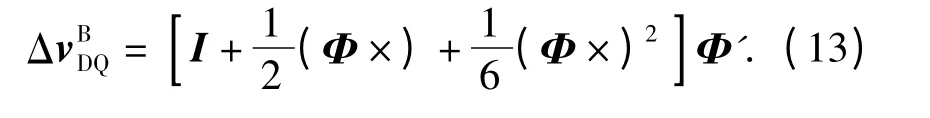
考虑到惯性器件的输出是增量形式，(10)式计算如下:

2 两种速度更新算法的精度比较

从第1 节的分析可以看出:传统速度更新算法计算速度增量时，在积分运算前忽略了二阶小量［Φ(t)×］2并对三角函数作了一阶近似;对偶四元数速度更新算法计算速度增量时，利用基于惯性器件输出定义的螺旋矢量给出了速度增量准确解，在导航解算中对速度增量准确解中的三角函数作了四阶近似。因此，两种算法得到的速度增量精度是不同的。

将(14)式代入(13)式，得到

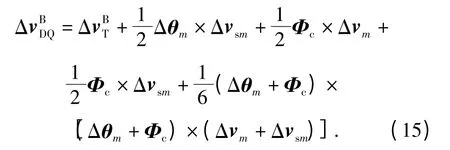
(15)式即为在对偶四元数导航算法中，利用惯性器件输出计算速度增量的结果。比较(15)式和(6)式，可看出，(15)式右端比(6)式多了4 项叉乘项，下面分析这4 项的影响。叉乘项中出现的Δvsm、Φc分别为划船误差、圆锥误差，当载体的角运动方向与线运动方向在空间不断变化时，即载体处于比较高动态环境下，Δ vsm、Φc是不为0 的整流误差项，这些整流误差与惯性器件输出的增量是不共线的，因此会造成(15)式右端的4 项叉乘项不为0，由此对导航精度产生影响，影响程度取决于载体所处动态环境的恶劣程度。

由上述分析可看出，对偶四元数速度更新算法的精度明显高于传统速度更新算法，精度优势体现在(15)式中右端后4 项。下面将定义两种误差，通过这两种误差对两种速度更新算法在精度上的不同作定量的分析。

2.1 两种误差的定义

传统速度更新算法中的速度增量表达式(5)式，是在忽略(2)式中二阶小量［Φ(t)×］2的前提下得到的，将由此引起的误差定义为截断误差

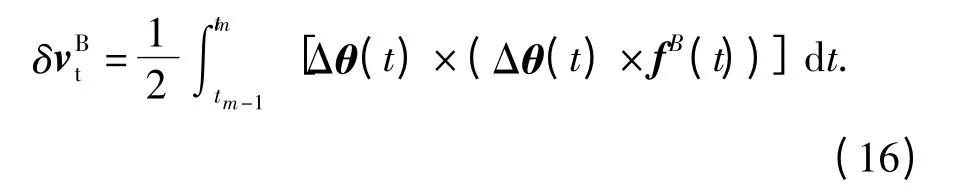
按照传统速度更新算法的实现思想，即使保留(2)式中的二阶小量［Φ(t)×］2，所得到的速度增量与对偶四元数算法中的速度增量相比也还是存在误差。前者计算速度增量时在积分运算之前对三角函数作了一阶近似，而后者是在求得速度增量准确解后对三角函数作了四阶近似。对于这种在积分运算前对表达式作近似和近似阶次低引起的误差，在此将其定义为近似积分误差

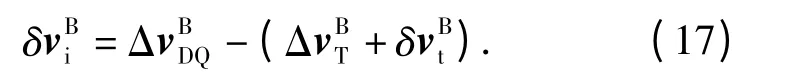
截断误差和近似积分误差的存在，导致传统速度更新算法比对偶四元数速度更新算法精度低。

2.2 两种误差的计算

以二子样速度更新算法为例，推导上述两种误差的定量计算公式，分析误差大小与载体运动的关系，并比较两种速度更新算法在精度量级上的差别。

在速度更新周期内，对载体的角速度和比力采用线性函数拟合

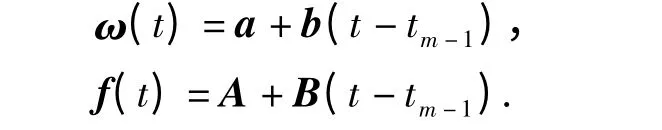
对于tm-1≤t≤tm，有

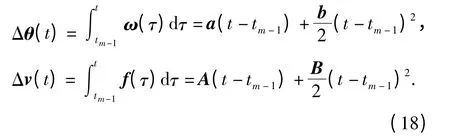
在［tm-1，tm］内等间隔采样两次，利用陀螺输出的角增量Δθm(i)，i =1，2，与加速度计输出的速度增量Δ vm(i)，i =1，2，可求得(18)式中的各项系数:

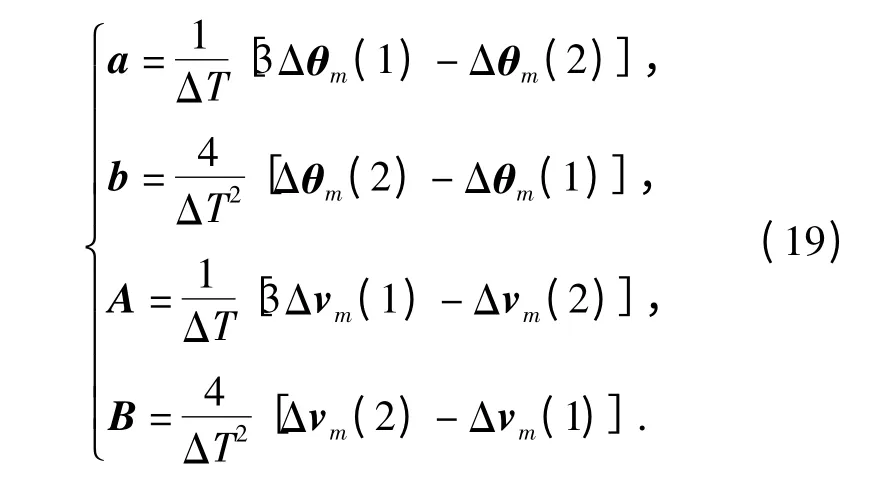
显然在ΔT 固定的情况下，系数a 和b、A 和B分别取决于陀螺、加速度计的输出增量值。下面就利用这些系数定量地分析传统更新算法中存在的两类误差。

将(18)式代入(6)式，得到二子样传统导航算法中速度增量的计算值

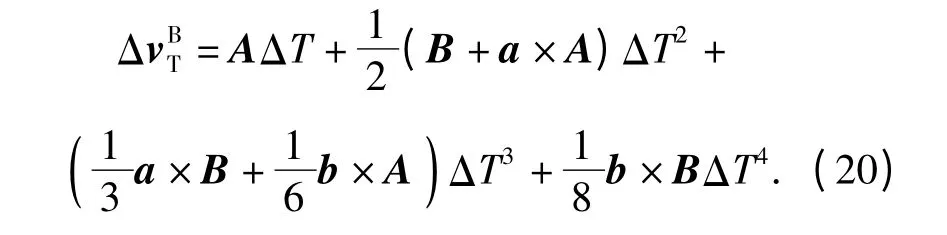
将(18)式代入(16)式，得到(20)式存在的截断误差为

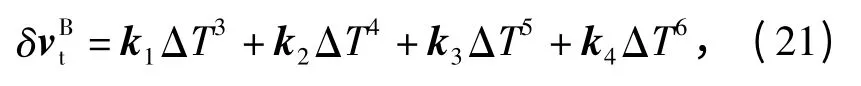
将(18)式代入(17)式，得到(20)式存在的近似积分误差为

若记

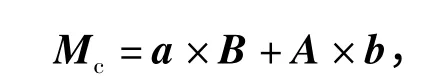
(22)式中的各项系数为:

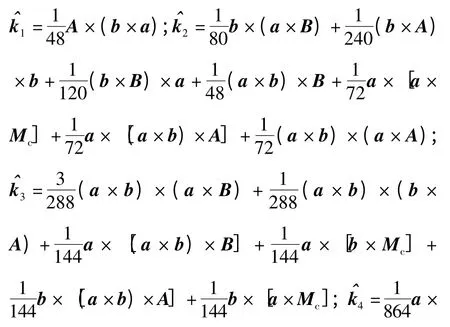
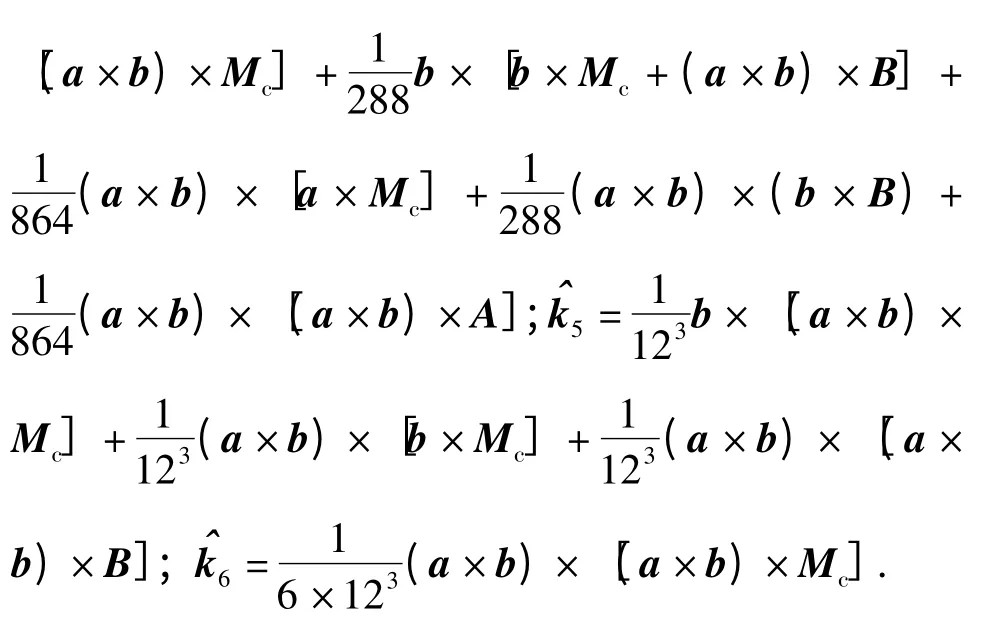
比较(20)式与(21)式、(22)式的结果可以看出:传统速度更新算法求得的速度增量ΔvBT近似到ΔT4，存在着比较明显的截断误差与近似积分误差，若载体处在高动态或大机动运动状态下，这两类误差会越发明显。

由(17)式可知

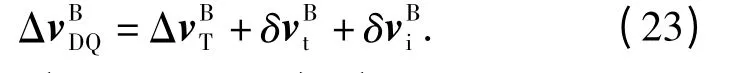
即(21)式与(22)式的和即是(15)式中右端后4项。可见，对偶四元数速度更新算法的计算精度等价于传统速度更新算法补偿了截断误差和近似积分误差后的计算精度，速度增量ΔvBDQ精确到ΔT9.在高动态或大机动运动环境下，对偶四元数算法在精度上的优势更显著，而且这种精度优势还随着算法子样数的增加而提高，如表1所示。表1中对各子样算法下，两种速度更新算法中速度增量所精确到的ΔT阶次进行了比较。

3 仿真分析

3.1 仿真环境

选东北天地理坐标系为导航坐标系，载体初始位置:经度110°，纬度40.5°，高度0 m.设置如下两种同时包含圆锥运动与划船运动的复杂动态测试条件。

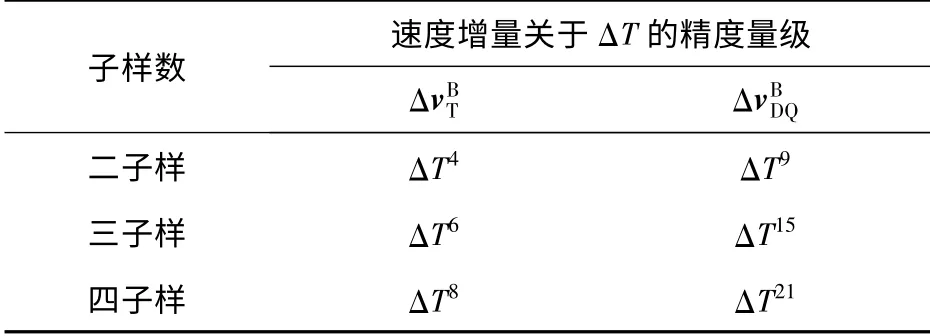
表1 两类速度更新算法的精度量级比较Tab.1 Comparison of accuracy magnitude orders between two velocity update algorithms

条件1 载体相对地球作幅值较大的三轴线振动与角振动，投影在导航系中的三轴线位移为S =投影在导航系中的载体姿态角分别为俯仰角航向角滚转角γ =

3.2 理想情况下的测试

不考虑惯性器件的测量误差，考察传统二子样导航算法与对偶四元数二子样导航算法的性能。

在条件1 下，取ΔT =0.5 s，仿真比较结果如图2～图7所示，图中绘出的是真实值减去计算值的误差曲线。图2～图4中能够清楚地看出两种算法导航参数误差的变化规律;随着导航时间的增长，如图5～图7所示，传统算法T 的导航误差发散的快且幅值远大于对偶四元数算法(DQ)，后者的精度优势非常明显。

在高动态条件2 下，取ΔT =0.002 s，两种二子样导航算法的仿真比较结果如图8～图10 所示，在此高动态环境下，沿Z 轴方向会有明显的划船整流误差，对偶四元数算法对此误差的抑制能力明显优于传统算法。

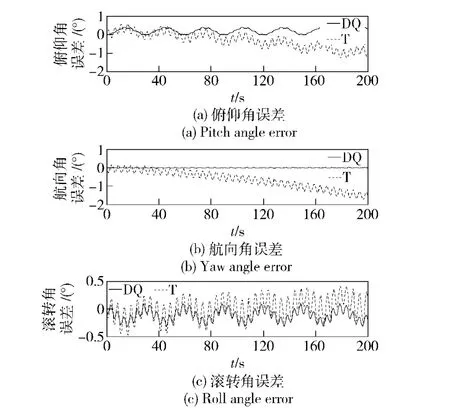
图2 条件1 理想情况下的姿态角误差(时间200 s)Fig.2 Attitude angle errors under ideal condition 1 (200 s)

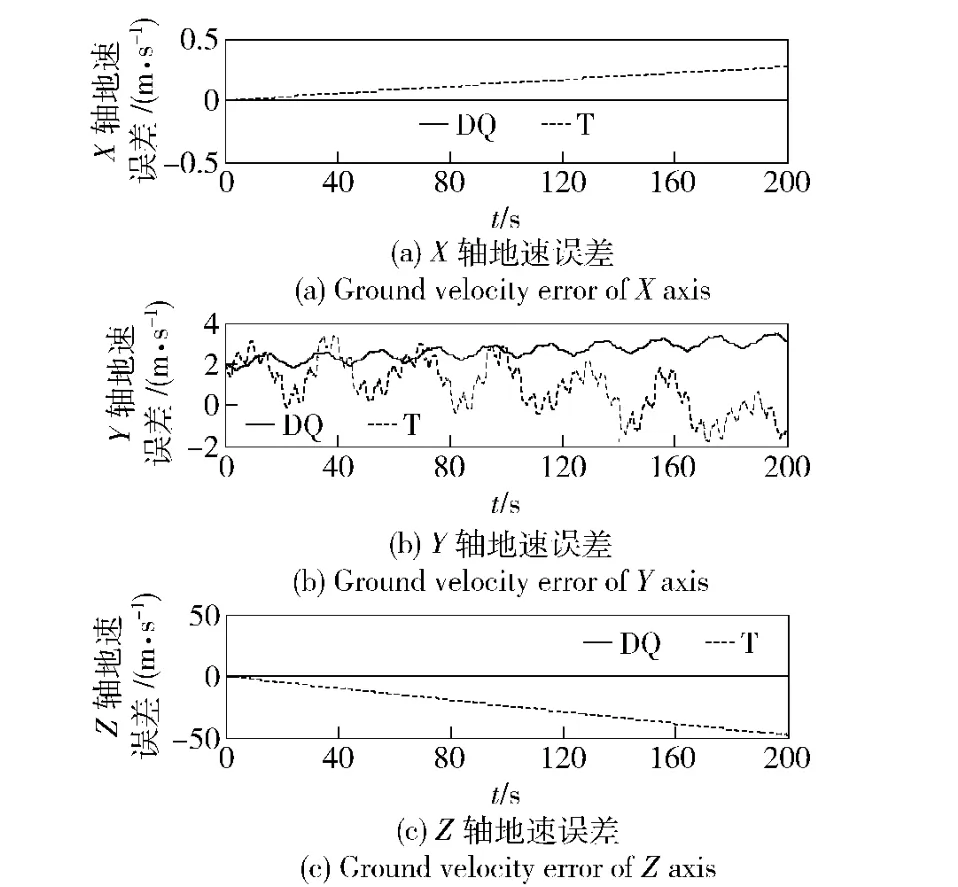
图3 条件1 理想情况下的地速误差(时间200 s)Fig.3 Ground velocity errors under ideal condition 1 (200 s)

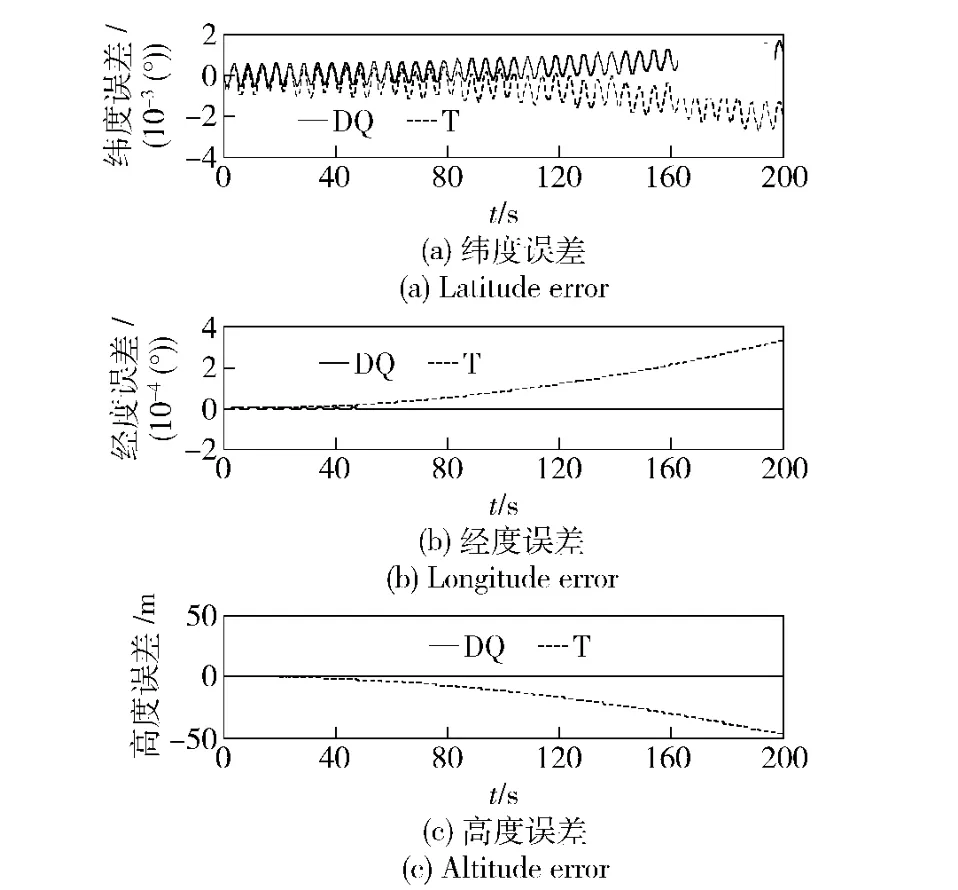
图4 条件1 理想情况下的位置误差(时间200 s)Fig.4 Position errors under ideal condition 1 (200 s)

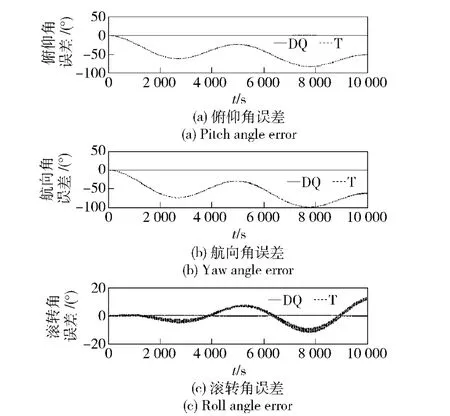
图5 条件1 理想情况下的姿态角误差(时间10 000 s)Fig.5 Attitude angle errors under ideal condition 1 (10 000 s)

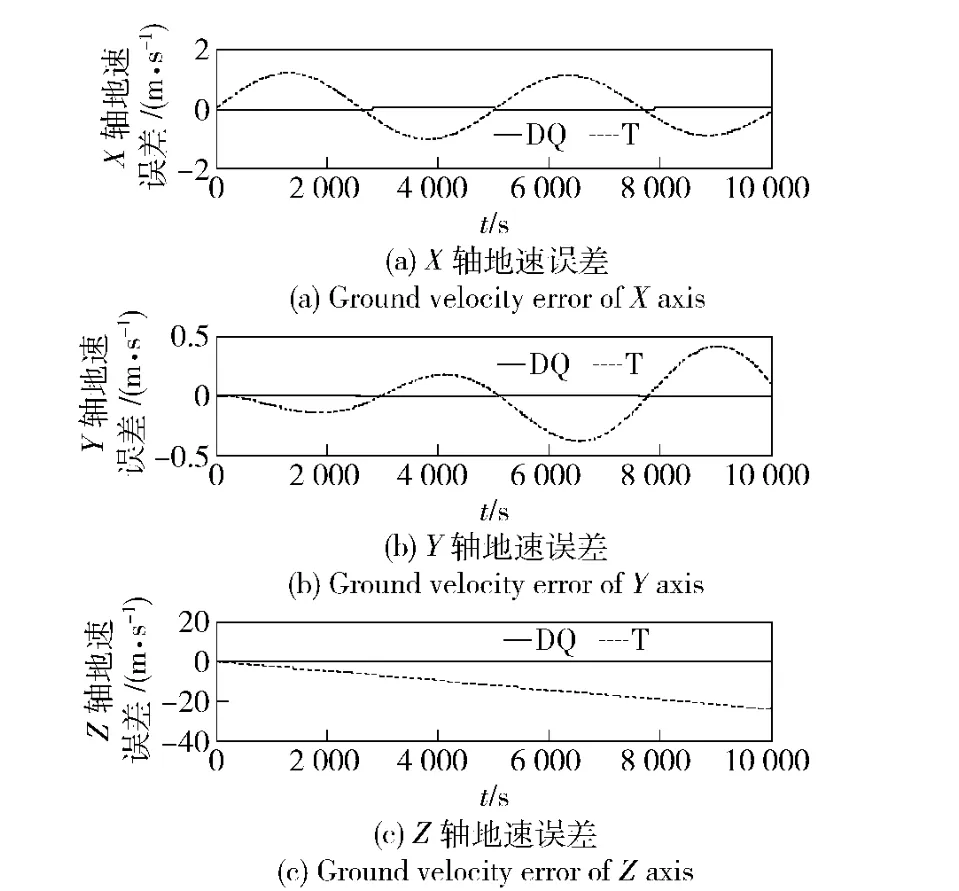
图6 条件1 理想情况下的地速误差(时间10 000 s)Fig.6 Ground velocity errors under ideal condition 1 (10 000 s)

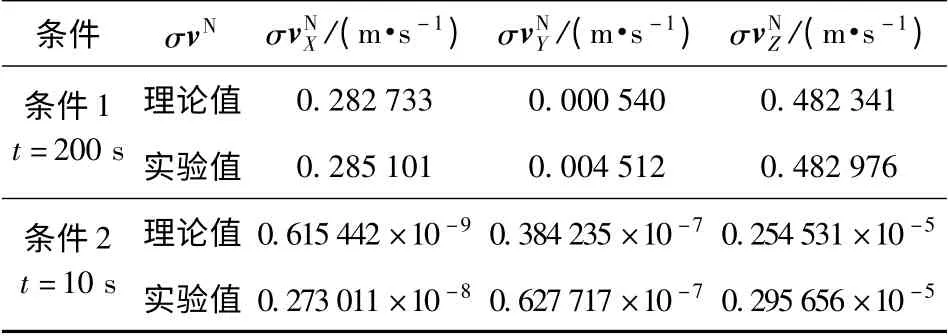
表2 理想情况下σvN 的理论值和实验值Tab.2 Both theoretical and experimental values of σvN in ideal case

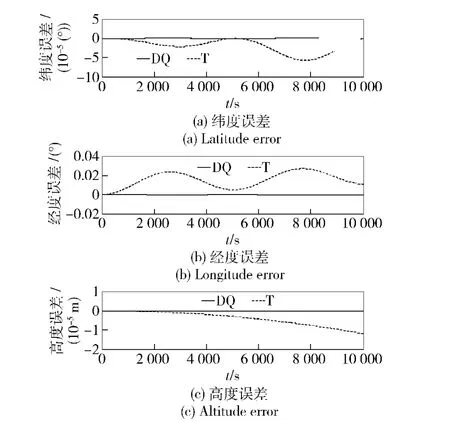
图7 条件1 理想情况下的位置误差(时间10 000 s)Fig.7 Position errors under ideal condition 1 (10 000 s)

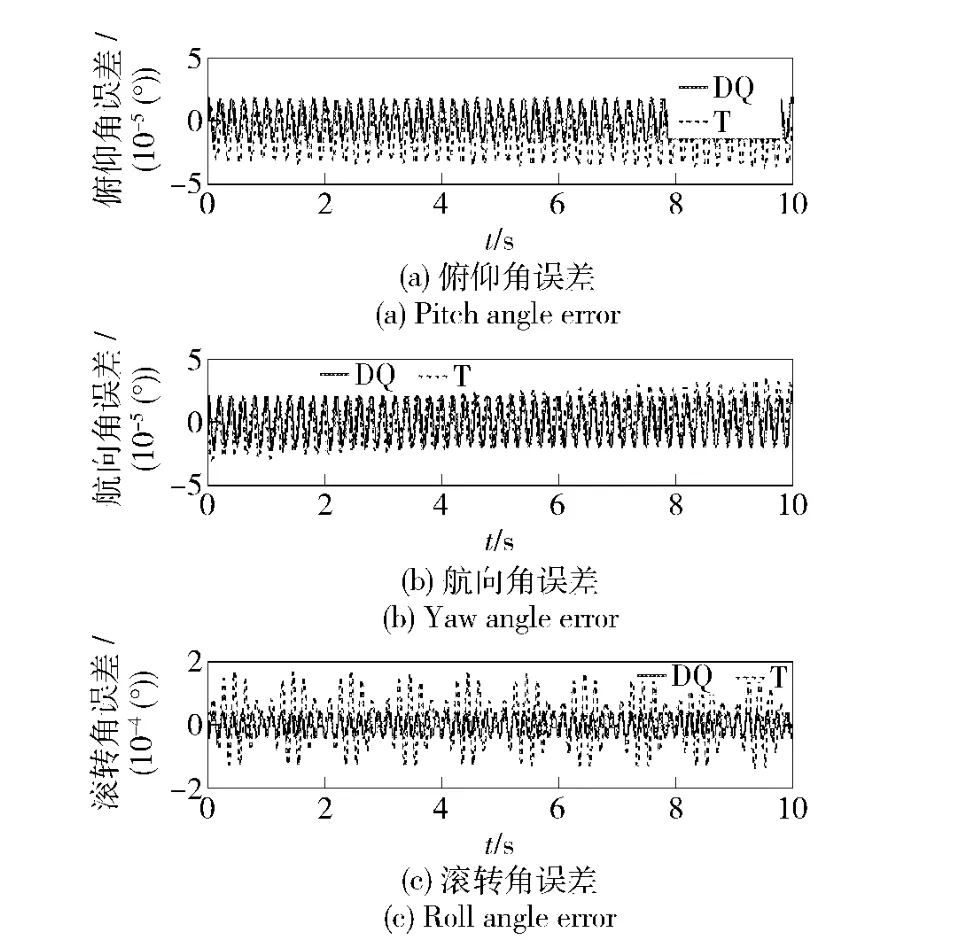
图8 条件2 理想情况下的姿态角误差Fig.8 Attitude angle errors under ideal condition 2

为了全面考察两种导航算法的性能，应对它们的运算效率进行考察。比较(6)式与(15)式可以看出，由于叉乘项的增多，导致对偶四元数导航算法的运算负担加大。以完成一个导航周期的运行时间为比较标准，分别对两种导航算法进行多次测试，平均运行时间的统计结果为δtDQ=3.88 ×10-4s(对偶四元数导航算法)，δtT=3.7 ×10-4s(传统导航算法).可见，与传统捷联导航算法相比，对偶四元数导航算法在牺牲较少运算效率的前提下，换来了精度上的显著优势。

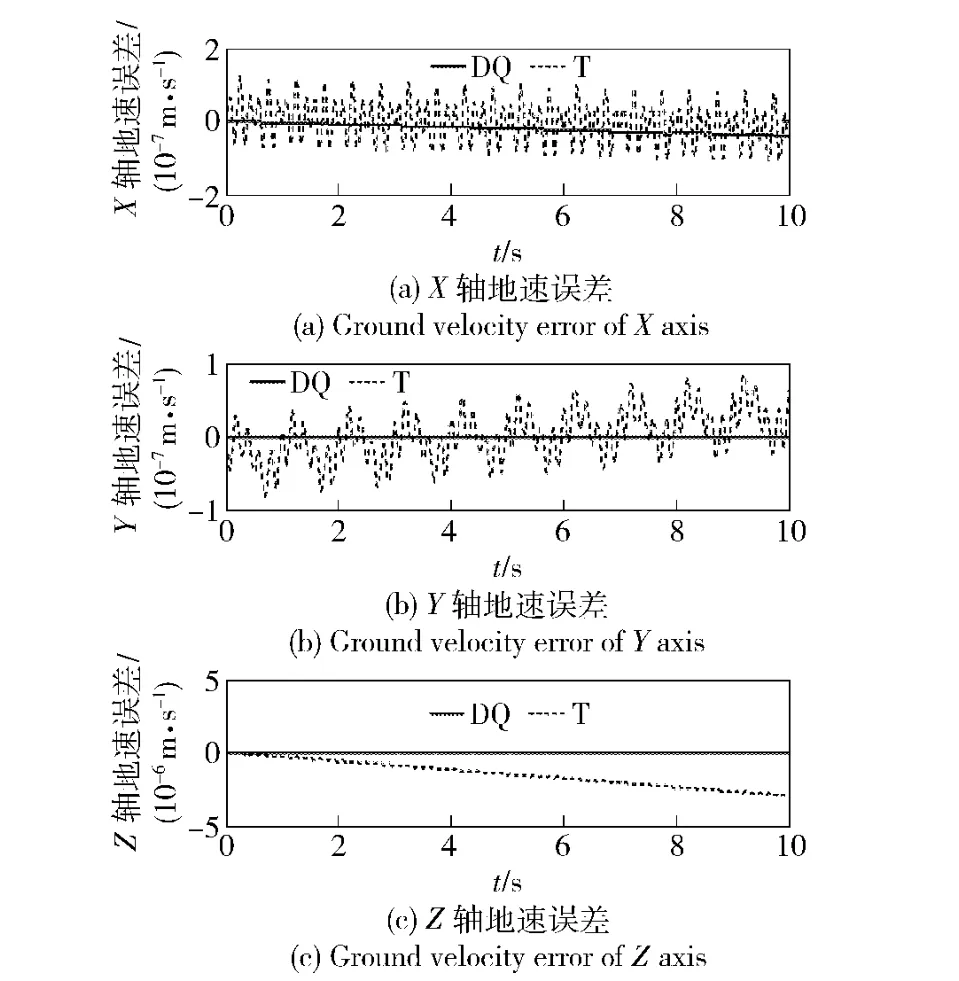
图9 条件2 理想情况下的地速误差Fig.9 Ground velocity errors under ideal condition 2

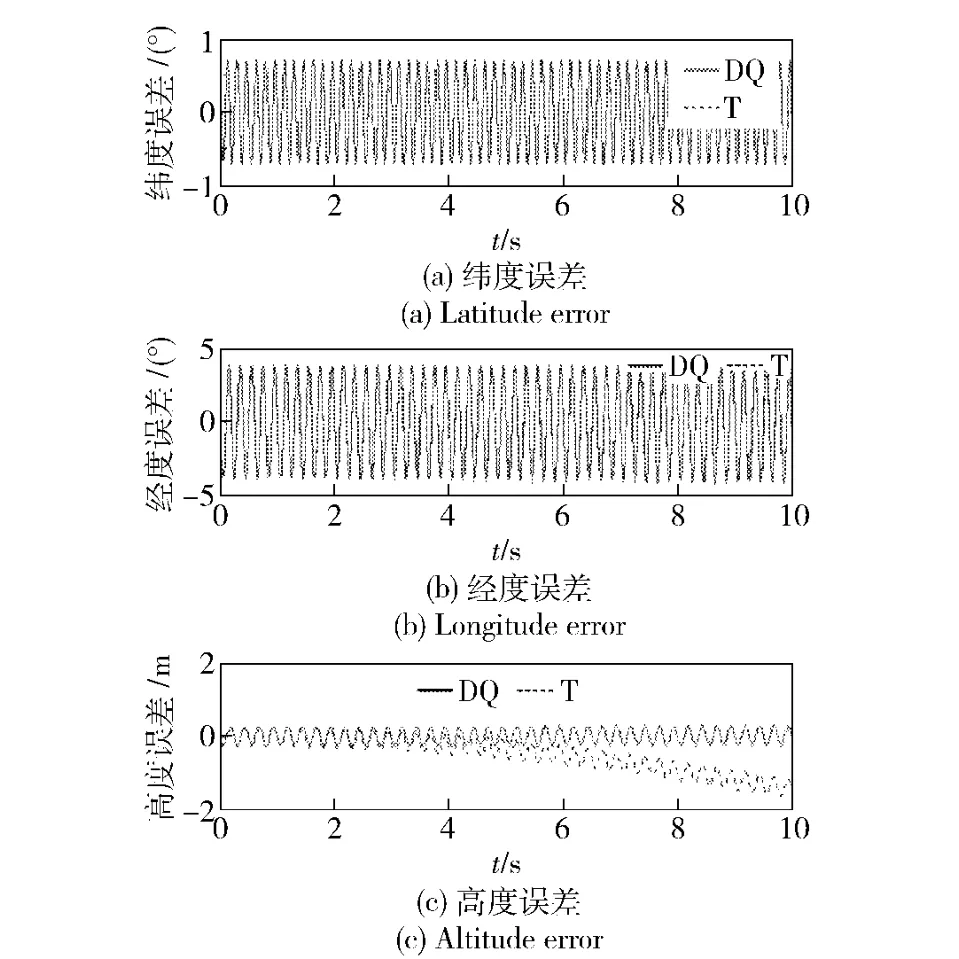
图10 条件2 理想情况下的位置误差Fig.10 Position errors under ideal condition 2

3.3 实际情况下的测试

考虑惯性器件的测量误差，并设定:

陀螺随机误差标准差σg=10-3°/h;加速度计随机误差标准差σa=10-5g，g 为重力加速度。

在条件1 下，取ΔT =0.2 s，两种导航算法的仿真比较结果如图11～图13 所示，与图2～图4中理想情况下的结果相比，可以看出:实际情况下的曲线出现了随机漂移，这种漂移在Y 轴地速误差与纬度误差曲线上比较明显。这是惯性器件测量误差随时间积累造成的影响，不过从总体看对偶四元数导航算法在精度上的优势仍然很明显。

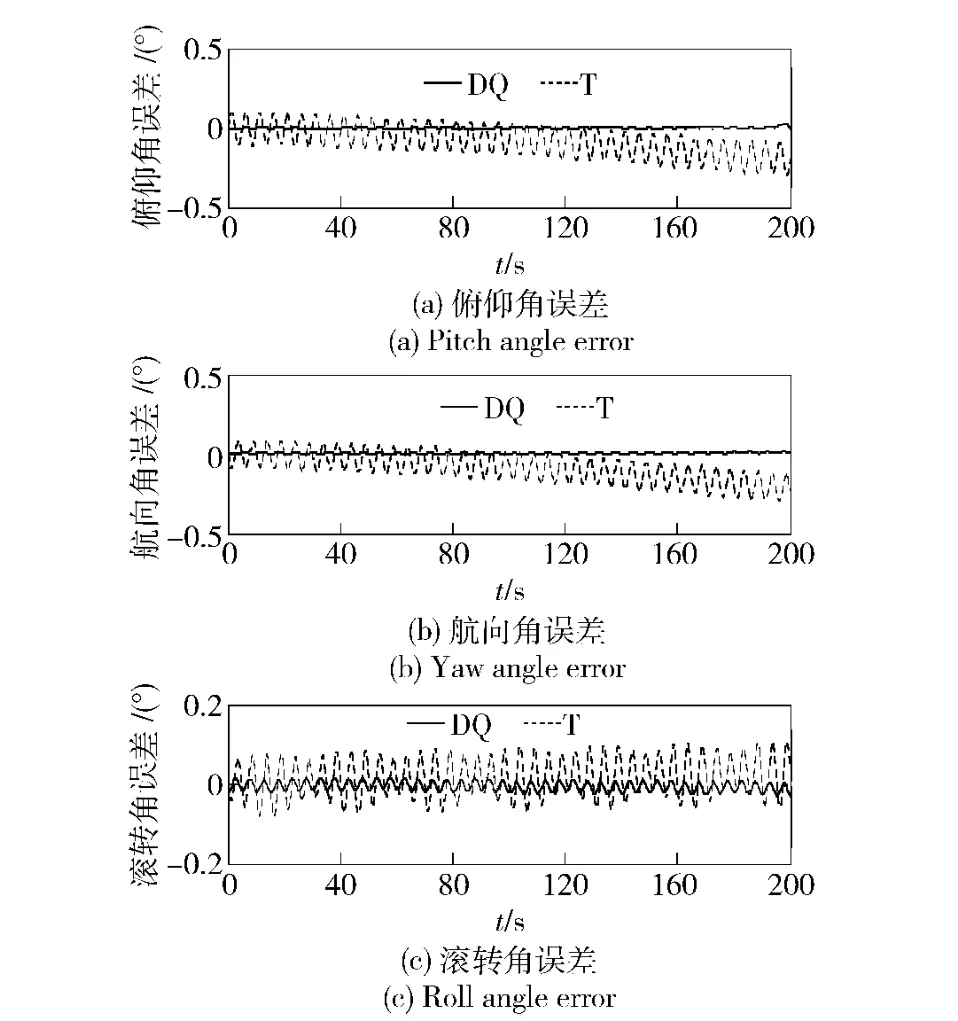
图11 条件1 实际情况下的姿态角误差(时间200 s)Fig.11 Attitude angle errors under real condition 1 (200 s)

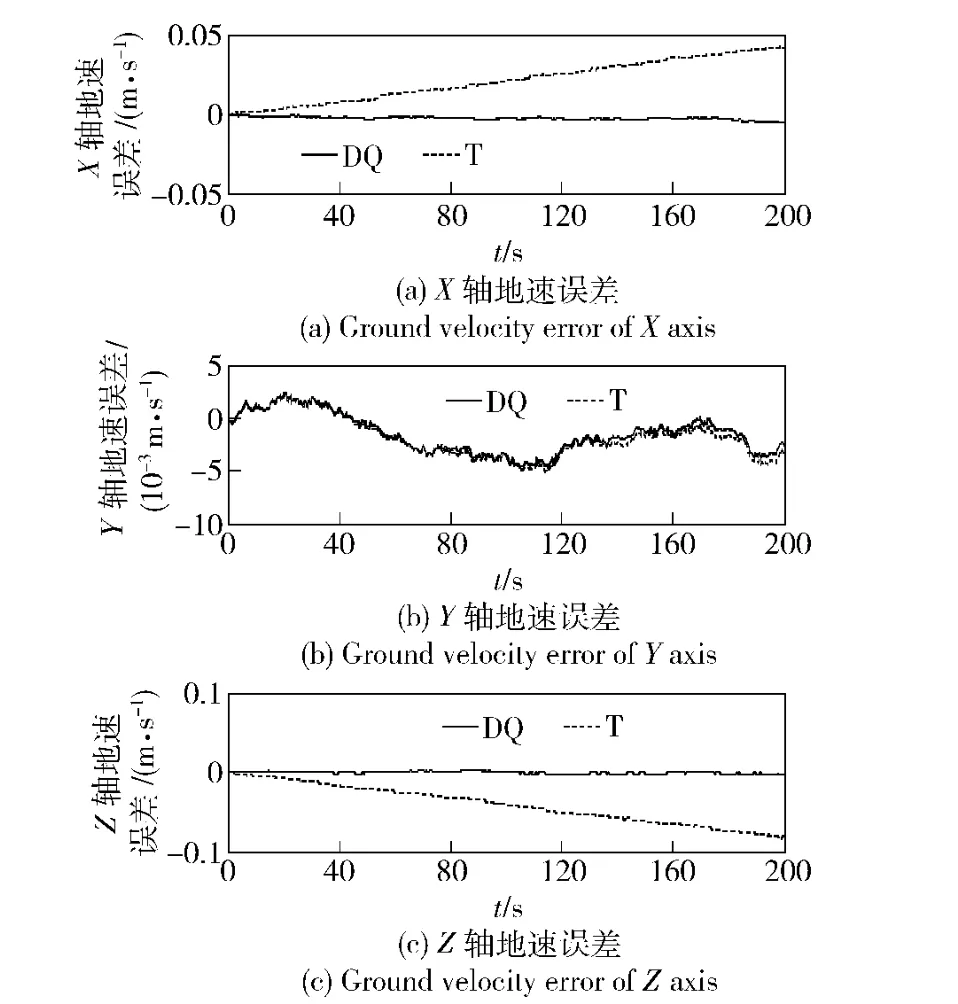
图12 条件1 实际情况下的地速误差(时间200 s)Fig.12 Ground velocity errors under real condition 1 (200 s)

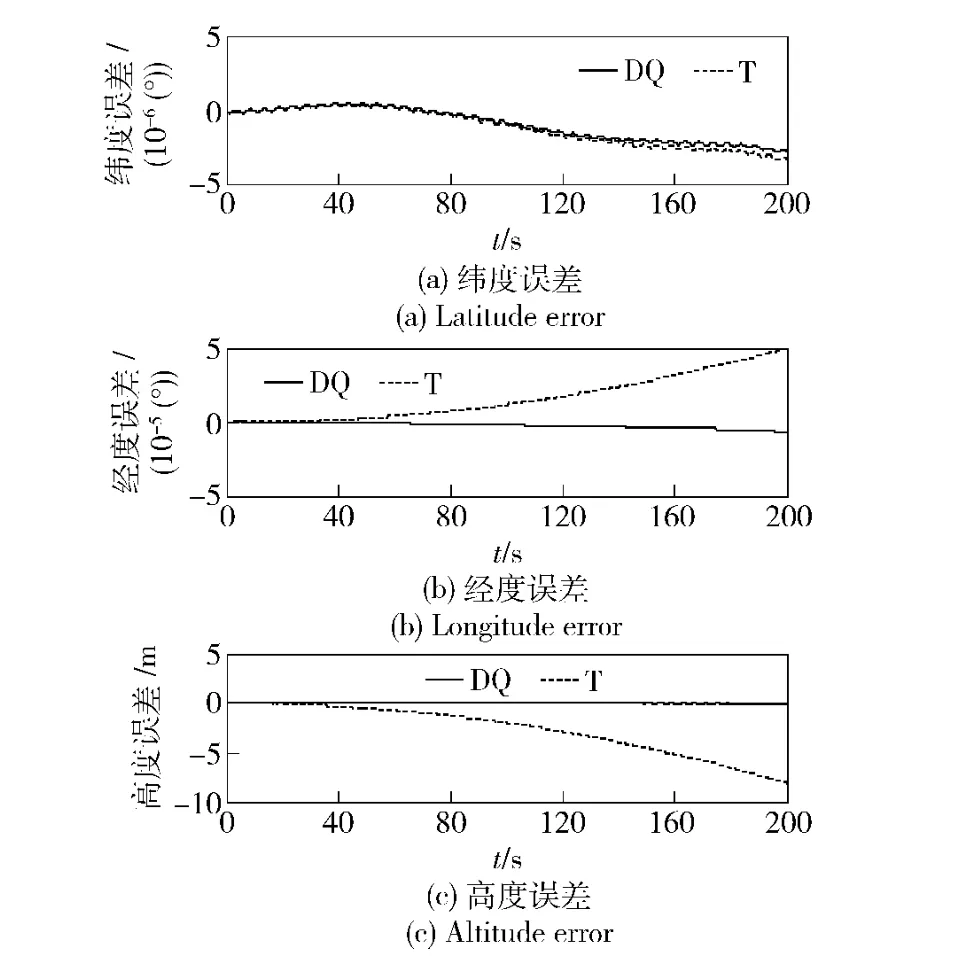
图13 条件1 实际情况下的位置误差(时间200 s)Fig.13 Position errors under real condition 1 (200 s)

对于高动态条件2，取ΔT =0.01 s，两种导航算法的仿真比较结果如图14～图15 所示。可以看出:由于惯性器件测量误差的积累影响，造成的导航参数随机漂移现象比条件1 严重，两种导航算法的性能从X 轴与Y 轴的导航参数结果难以区分;不过随着导航时间的增长，从Z 轴上抑制整流误差的能力上可以看出对偶四元数的精度优势会逐渐显著。逐级降低惯性器件测量精度，保证其他高动态测试条件不变，当测试时间t =400 s 时，两种导航算法的Z 轴地速误差比较结果如表3所示，可得出结论:在惯性器件的测量输出能够比较准确地反映高动态运动信息时，对偶四元数导航算法的性能始终优于传统导航算法;反之，当惯性器件精度下降不能保证上述条件时，两种导航算法精度降低到一致。

4 结论

针对捷联惯导系统，对传统的速度更新算法和对偶四元数速度更新算法进行了对比与研究，通过定义两类误差(截断误差和近似积分误差)，定性地分析了对偶四元数速度更新算法较传统速度更新算法在精度上的优势，并对两种算法的精度差别进行了定量的计算。结论的正确性通过理想情况下与实际情况下的仿真测试得到了验证。

在捷联惯导系统中，速度更新算法的精度高，必然获得高精度的位置导航信息，进而通过修正导航坐标系提高载体姿态的确定精度。所以，对偶四元数速度更新算法在精度上的优势，提高了对偶四元数捷联惯导算法的整体性能优势，这一点已通过两种情况下的仿真测试得到了充分验证。

References)

［1］ Savage P G.Strapdown inertial navigation integration algorithm design part 2:velocity and position algorithms［J］.Journal of Guidance，Control and Dynamics，1998，21(2):208 -221.

［2］ Savage P G.Strapdown inertial navigation integration algorithm design part 1:attitude algorithms［J］.Journal of Guidance，Control and Dynamics，1998，21(1):19 -28.

［3］ Connolly T H，Pfeiffer F.Cooperating manipulator control using dual quaternion coordinates［C］∥Proceedings of the 33rd Conference on Decision and Control.Lake Buena Vista:IEEE，1994:2417 -2418.

［4］ Daniilidis K，Bayro-Corrochano E.The dual quaternion approach to hand-eye calibration［C］∥Proceedings of ICPR ’96.Vienna:IEEE Computer Society Press，1996:318 -322.

［5］ Dai J S.An historical review of the theoretical development of rigid body displacements from Rodrigues parameters to the finite twist［J］.Mechanism and Machine Theory，2006，41(1):41 -52.

［6］ Erhan Ata，Yusuf Yayli.Dual quaternions and dual projective spaces［J］.Chaos，Solitons ＆ Fractals，2009，40(3):1255 -1263.

［7］ Leonardo Traversoni.Interpolating movements using CAGD tools［C］∥Proceeding of CGIV 2007，Bangkok:IEEE Computer Society Press，2007:229 -238.

［8］ 武元新.对偶四元数导航算法与非线性高斯滤波［D］.长沙:国防科学技术大学，2005.WU Yuan-xin.Research on dual-quaternion navigation algorithm and nonlinear gaussian filtering［D］.Changsha:National University of Defense Technology，2005.(in Chinese)

［9］ 孙枫，奔粤阳.捷联惯导算法中螺旋理论的应用［J］.系统工程与电子技术，2007，29(9):1533 -1535.SUN Feng，BEN Yue-yang.Application of spiral theory in strapdown inertial navigation algorithm［J］.Systems Engineering and Electronics，2007，29(9):1533 -1535.(in Chinese)

［10］ 杨伟光.捷联惯性导航系统动态误差标定与补偿算法研究［D］.长沙:国防科学技术大学，2009.YANG Wei-guang.Study on calibration and compensation of dynamic errors in SINS［D］.Changsha:National University of Defense Technology，2009.(in Chinese)

［11］ 吴高龙，刘华伟.对偶四元数导航的简化算法［J］.应用科学学报，2010，28(6):646 -654.WU Gao-long，LIU Hua-wei.Simplified dual-quaternion navigation algorithm［J］.Journal of Applied Sciences，2010，28(6):646 -654.(in Chinese)