基于F分布的指数型产品环境因子计算方法研究

程红伟，陶俊勇，张云安，陈循

(国防科学技术大学 装备综合保障技术重点实验室，湖南 长沙410073)

0 引言

在工程实际中当产品的寿命分布服从指数分布时常称其为指数型产品。研究表明:大部分电子、机电产品寿命分布均服从指数分布。现代产品研制往往面临产品复杂度增加、研制成本和可靠性要求高、研制周期短、投入可靠性试验的样本量小、不同研制阶段的试验环境不同等诸多问题，因此如何有效地解决小子样、变环境产品可靠性评估是现阶段可靠性工程面临的难题之一。环境因子方法属于多源信息融合方法的一种［1］，其能够直观地融合各种试验信息对产品的可靠性进行分析与评估，是解决小子样、变环境产品可靠性评估的有效途径之一。文献［2］详细分析了可靠性评估中环境因子的发展过程，文献［3］给出了指数型产品环境因子的概念，进一步明确了指数型产品环境因子的物理意义。文献［4］给出了指数型产品环境因子的信仰分布，进而得到了环境因子的Bayes 算法。文献［1］给出了指数型产品环境因子的区间估计，得到了产品可靠性的区间估计。文献［5］给出了一种零故障情况下指数型数据环境因子的计算方法。

对于指数型产品而言，环境因子的物理意义十分明确，即相同产品在不同环境下的失效率之比。但环境因子的准确计算一直是指数型产品可靠性评估的难点。文献［6］根据指数型产品试验统计量服从χ2分布的特点，以及χ2分布与F 分布之间的关系给出了环境因子的算法，并进一步分析了小样本情况下该算法的不足及改进思路。在上述研究的基础上，本文提出了修正因子的概念，并将其引入到环境因子的计算公式中，提高了指数型产品环境因子的计算精度。

1 指数型产品环境因子算法

1.1 假设与定义

产品可靠性评估中环境因子算法是基于以下3个假设［3］:

1)在不同的应力水平下，产品的失效机理保持不变;

2)在不同的应力水平下，产品的寿命分布形式保持不变;

3)相同产品在不同环境下工作时，当累积失效概率相同时，则产品内在的累积损伤相同。

基于以上假设，指数型产品环境因子的定义［4］如下:指数型产品较严酷试验环境设为环境1，产品的失效率为λ1;较良好的试验环境设为环境2，产品的失效率为λ2.环境2 相对于环境1 的环境因子K12(以环境1 为基准)定义为:环境1 下产品的失效率与环境2 下产品的失效率之比，即

同理可得环境1 相对于环境2 的环境因子K21(以环境2 为基准)为K21=λ2/λ1.

显然环境因子K12越大，表示环境2 相对于环境1 而言，其试验条件越良好;反之，则表示环境2 的试验条件越严酷。此外，对于指数型产品，基于环境因子的可靠性评估中对同母体变环境、变母体同环境和变母体变环境3 种类型的试验数据都适用，拓展了指数型产品环境因子可靠性评估方法［6］。

1.2 基于F 分布的计算方法

假定某指数型产品，在环境1 中投入n1个产品进行定数截尾寿命试验，结果为(T1，r1);在环境2中投入n2个产品进行定数截尾寿命试验，结果为(T2，r2)，Ti为环境i 产品累积试验时间，ri为环境i产品寿命试验的累积失效次数，i=1，2.

由定理［7］:设t1≤t2≤…≤tr是来自指数分布截尾数为r 的定数截尾样本，则总试验时间T 服从Γ(r，1/θ)分布，其2/θ 倍服从自由度为2r 的χ2分布:

由此可得:2λ1T1～χ2(2r1)，2λ2T2～χ2(2r2).

由χ2分布和F 分布之间的关系得

在产后42天，顺产的女性生殖系统逐渐恢复到孕前状态，而剖宫产的女性可能在产后8周恢复。不管剖宫产还是自然分娩，喂奶充分的产妇，恢复排卵的时间晚，雌激素水平稍低，阴道黏膜层较薄，宫颈分泌的黏液较少，产后第一次性生活时，有人感觉干涩或者疼痛，以后逐渐恢复正常，大部分夫妻感觉性生活质量与孕前无变化。

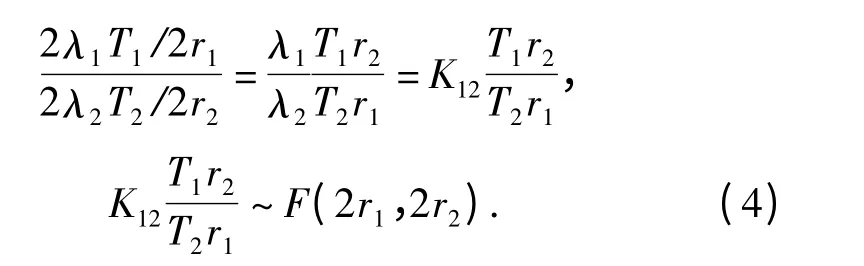
同理:

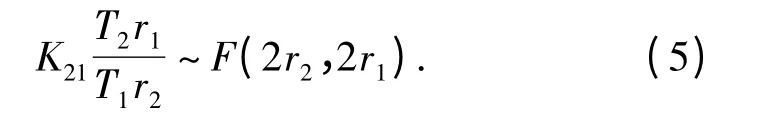
文献［6］指出该环境因子算法存在一定的问题，即小样本情况下以较良好环境(环境2)为基准环境得到的环境因子K 精度较高，而以较严酷环境(环境1)为基准环境得到的环境因子精度低。

针对以上问题，分析了基于F 分布的环境因子算法在大样本和小样本情况下的差异。

首先，由分布曲线进行直观分析。假设以较严酷的环境1 为基准环境，如(4)式所示，定义

得a12K12～F(2r1，2r2).

假设以较良好环境2 为基准环境，如(5)式所示，定义

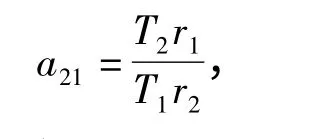
得a21K21～F(2r2，2r1).

以下通过实例数据对此进一步分析。如图1和图2所示，分别给出了大样本情况下和小样本情况下aK 的概率密度曲线。比较图1和图2可知:在大样本情况下，将a12K12的分布概率密度曲线，通过坐标变换和归一化处理后与a21K21的分布概率密度曲线接近程度较高;而在小样本情况下二者却存在很大差异。进而直观地说明了小样本情况下，直接应用基于F 分布的方法所求得的和并非近似互为倒数的原因。

图1 大样本数情况下a21K21概率密度曲线Fig.1 The probability density curves in the case of large-scale samples

当随机变量X 服从非中心参数δ=0，自由度为(m，n)的F 分布，其概率密度函数［8］为

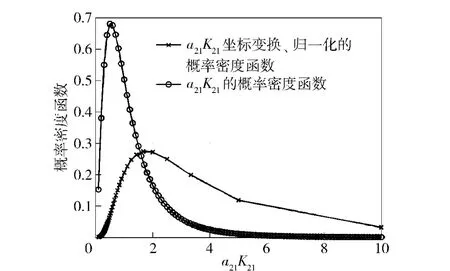
图2 小样本情况下a21K21概率密度曲线Fig.2 The probability density curves in the case of small-scale samples

其均值［9］为

将指数型产品寿命试验统计量a12K12和a21K21分别带入(6)式得

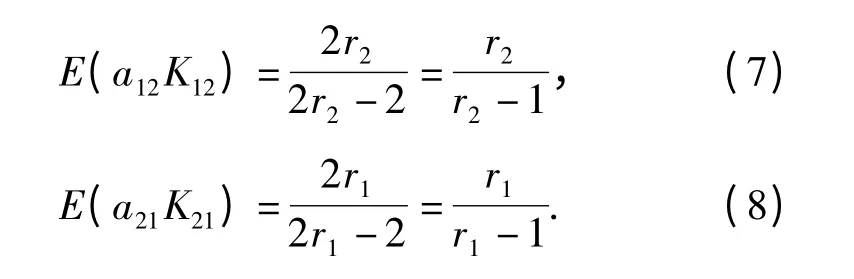
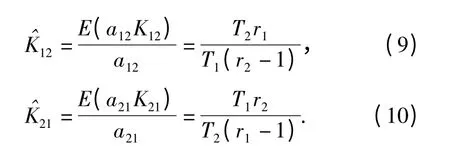
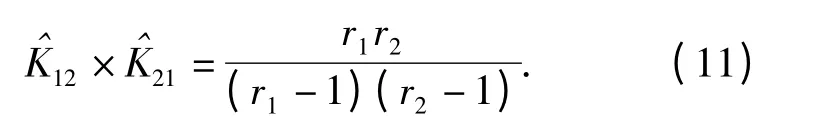
由(11)式得出，在大样本(r1≫1，r2≫1)情况下，×≈1;但在小样本情况下明显有×＞1.由此，进一步从理论上说明了基于F 分布的环境因子算法存在的问题。

1.3 计算方法修正

根据指数型产品环境因子的定义有:K12≥1，K21≤1，以下分析了估计值和的可信度，假设成立，则

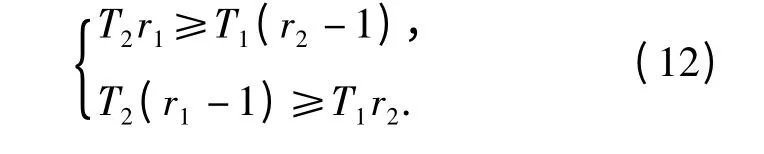
通过分析，如果T2r1≥T1(r2- 1)成立，则T2(r1-1)≥T1r2不一定成立;反之，如果T2(r1-1)≥T1r2成立，则T2r1≥T1(r2-1)必然成立。

根据指数型产品环境因子的定义可知

但由1.2 节可知，在小样本情况下(13)式并不成立，且二者之间存在较大的差值，且由前可知可信程度高于因此，在进行两个估计量调整时，要根据二者的可信程度按权值进行相应调整。小样本情况下，有二者的差值为

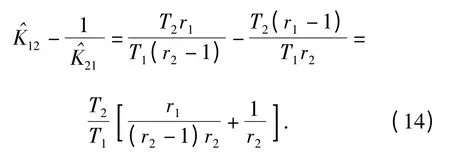
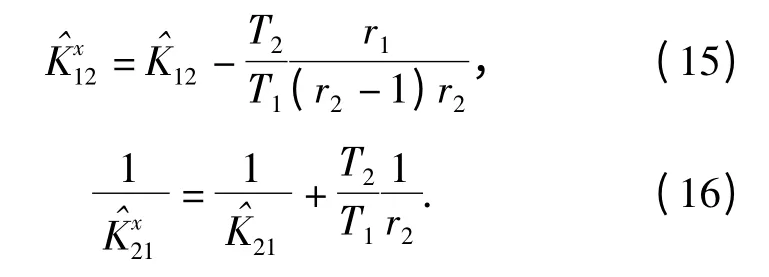
2 算例

假设某指数型产品分别在较严酷的环境1 和较良好的环境2 下进行定数截尾试验，所得试验数据如表1所示。

表1 某产品定数截尾试验数据Tab.1 Fixed number truncated test of a product

由表1可知T1=1 504 h，r1=8;T2=1 867 h，r2=4.将数据带入(9)式得

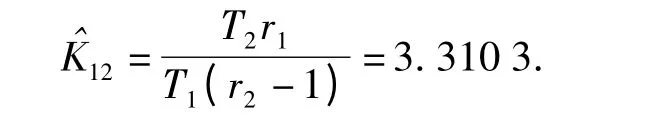
将数据带入(10)式，得

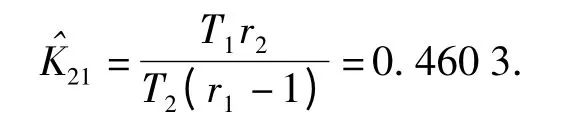
由K12和K21互为倒数，得

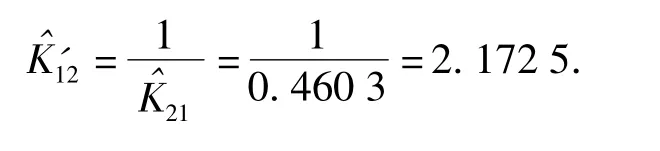
表1中的试验数据由Matlab 产生，且环境2 相对于环境1 的环境因子理论值为2.5.由此发现根据(9)式、(10)式计算得到的环境因子误差较大，且的计算误差为32.4%计算误差为13.2%，需进行进一步的修正，同时也将验证了比可信度高这一结论。

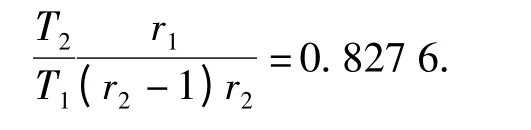
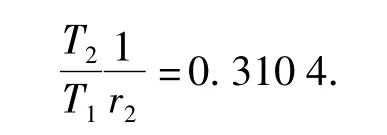
将修正因子代入(15)式和(16)式中得到修正后的环境因子估计值:

3 结论

本文根据指数型产品环境因子的定义和物理意义，指出基于环境因子的可靠性数据融合方法同样适用于变母体试验数据，从而简化了变母体试验数据的处理过程，拓展了指数型产品环境因子的适用范围。

在理论分析和仿真结果的基础上，指出现有指数环境因子计算方法在处理小样本数据时存在的缺陷，并给出了修正算法。通过仿真算例验证了修正方法的有效性。该方法弥补了传统方法在处理小样本数据时的不足，为解决指数型产品小样本、变母体、变环境可靠性评估问题提供了有效的方法。

References)

［1］ 甄昕.环境因子在电子产品可靠性评定中的应用研究［J］.电子产品可靠性与环境试验，2009，(1):20 -22.ZHEN Xin.Study on the application of the environmental factor in the reliability evaluation of electronic products［J］.Electronic Product Reliability and Environmental Testing，2009，(1):20 -22.(in Chinese)

［2］ 赵婉，温玉泉.可靠性评估领域中环境因子的研究进展［J］.电子产品可靠性与环境试验，2005，(2):69 -71.ZHAO Wan，WEN Yu-quan.The research status of environmental factor in reliability assessment［J］.Electronic Product Reliability and Environmental Testing，2005，(2):69 -71.(in Chinese)

［3］ 张春华，陈循，杨拥民.常见寿命分布下环境因子的研究［J］.强度与环境，2001，(4):7 -11.ZHANG Chun-hua，CHEN Xun，YANG Yong-min.Research on environmental factors of common life distributions［J］.Structure ＆Environment Engineering，2001，(4):7 -11.(in Chinese)

［4］ 刘琦，冯静，周经伦，等.指数分布环境因子的Bayes 算法［J］.电子产品可靠性与环境试验，2003，(3):42 -44.LIU Qi，FENG Jing，ZHOU Jing-lun，et al.The Bayesian method for environmental factor of exponential distribution calculation［J］.Electronic Product Reliability and Environmental Testing，2003，(3):42 -44.(in Chinese)

［5］ 李湘宁，王健.零故障情况下指数型数据环境因子计算方法［J］.火力与指挥控制，2009，34(10):60 -65.LI Xiang-ning，WANG Jian.The calculation method for environmental factor of exponential datum in zero failure［J］.Fire Control＆ Command Control，2009，34(10):60 -65.(in Chinese)

［6］ 程红伟，陶俊勇，张云安.指数分布环境因子算法探讨［C］∥2010年全国机械可靠性学术交流会论文集.湘潭:中国机械工程学会，2010:199 -202.CHENG Hong-wei，TAO Jun-yong，ZHANG Yun-an.Research on exponential distribution environmental factor［C］∥National Mechanical Reliability Academic Exchange Meeting.Xiangtan:Chinese Mechanical Engineering Society，2010:199 -202.(in Chinese)

［7］ 陈循，陶俊勇，张春华，等.机电系统可靠性工程［M］.长沙:国防科学技术大学出版社，2010.CHEN Xun，TAO Jun-yong，ZHANG Chun-hua，et al.Electromechanical systems reliability engineering［M］.Changsha:National University of Defense Technology Press，2010.(in Chinese)

［8］ 陈希孺.数理统计引论［M］.北京:科学出版社，1981.CHEN Xi-ru.Introduction of mathematical statistics［M］.Beijing:Science Press，1981.(in Chinese)

［9］ Dai J，Das D，Pecht M.Prognostics-based health management for free air cooling of data centers［C］∥IEEE Prognostics and Health Management Conference.Macau:IEEE，2010:1 -6.