改进的分层边际算法优化备件的初始配置方案

阮旻智，李庆民，，李承，黄傲林

(1.海军工程大学 科研部，湖北 武汉430033;2.海军工程大学 兵器工程系，湖北 武汉430033;3.海军工程大学 导航工程系，湖北 武汉430033)

0 引言

备件是装备维护检修和应急处理的保障性物资，是影响装备战备完好性及其作战能力的重要因素。初始备件是装备形成战斗力的初始保障期内装备使用与维修所需要的备件，在装备列装服役初期，由承制方同步交付部队，在采购装备的同时，军方需要与承制方协商来确定初始备件的种类和数量，即所谓的装备初始配置问题［1］。因此，合理规划备件的初始配置方案是降低装备寿命费用、提高保障效能的有效途径。对于故障率高、消耗量(报废率)低、价格昂贵的修复性备件，多级维修供应是一种较为科学的备件管理模式。但多级保障模式下的备件配置优化是大规模、非线性的NP 难问题［2］，模型求解需要在多站点、多层次、多系统等问题之间进行协同规划，因此，寻求合理的优化算法是关键。文献［3］运用相关回归技术寻求备件的最优配置;文献［4］引入拉格朗日乘子对模型进行分解，采用启发式算法求解备件的订购策略。目前，边际优化算法［5］是求解该类问题最为常见的一种方法，该方法是一种渐进的优化技术，用于分配短缺资源来获得最大效益。近些年，随着计算机及人工智能技术的发展，如仿真优化方法［6］、启发式算法［7］、BP 神经网络［8］、遗传算法［9］、粒子群算法［10］等也曾先后被应用于备件模型的求解。

相比而言，启发式算法能够在较短时间内得到备件方案的最优结果，通常被用于计算备件的订购方案;仿真方法可以在设计上考虑各项随机因素，其结果可信度较高，被广泛应用于备件方案的评估与验证，如瑞典开发的SIMLOX 软件就是基于离散事件的仿真系统，采用蒙特卡洛方法对备件方案进行评估;遗传、粒子群等进化算法优化速度快、效率相对较高，但该算法缺乏备件方案的费效全过程分析能力;边际优化算法操作简单、结果精度高，其最大优势在于算法迭代的整个过程中不丢失最优解［11］，能够得到方案的最优费效曲线。瑞典开发的OPUS10、美国开发的VMETRIC 等备件优化系统，都将边际优化算法作为核心算法，但该算法的突出问题是优化效率低。

本文针对多级维修供应模式下，针对多层次结构的串联系统，在传统边际算法的基础上，提出一种改进的分层边际优化算法对初始备件配置进行优化。

1 备件初始库存配置模型

1.1 备件需求率预测

设m=1，2，…，M 为保障站点编号，j =1，2，…，J 为备件项目编号，则备件j 在站点m 的需求率λmj由两部分构成［12］:

1)站点m 所保障的所有下一级别站点l(l∈Unit(m))对故障件j 不能维修的数量之和;这些不能维修的故障件需要送到站点m 进行维修。

2)站点m 对故障件j 的母体l(l∈Aub(j))进行维修时，其发生对备件j 的需求次数。

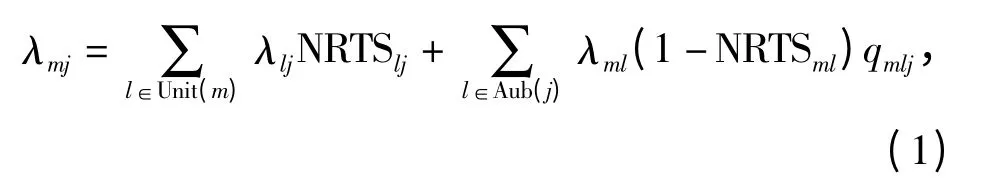
式中:NRTSmj为站点m 不能对故障件j 进行修复的比例;qmlj为故障隔离率，即故障件l 在站点m 进行维修时，发生对l 的分组件j 的需求占故障件l 维修次数的比例。

备件需求率可根据(1)式进行递推，递推的开始是从使用现场的LRU 进行，可根据装备配置量、系统结构、站点维修条件等参数确定，则LRUj在使用现场的年平均需求率

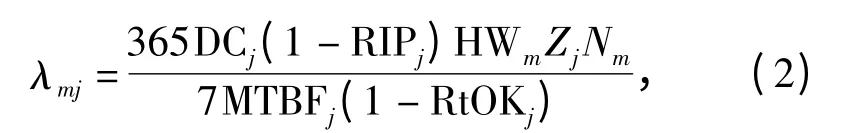
式中:m∈Echelon(N);j∈Inden(1);DCj为占空比;RIPj为原位维修率;HWm为装备的平均周工作时间(h);Zj为部件j 的单机安装数;Nm为装备配置量;MTBFj为组件j 的平均故障间隔时间;RtOKj为重测完好率。

1.2 备件供应渠道模型

备件供应渠道决定了备件短缺数的大小［13］，而备件短缺数将直接影响装备可用度和维修供应效能，因此确定备件供应渠道均值与方差是备件库存配置优化建模的核心。

1)故障件的在修数量:λmj(1 -NRTSmj)tmj，tmj为故障件j 的平均修复时间;

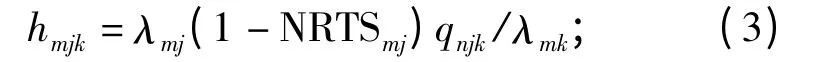
3)正在进行补给中的备件数量:λmjNRTSmjOmj，Omj为站点m 向上级申请备件的延误时间;

4)补给延误的备件数量:fmjEBOSUP(m)，j，fmj为影响站点m 的短缺占备件短缺总数的比例。

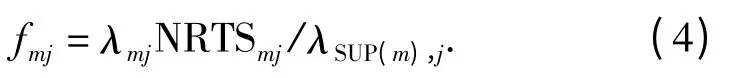
备件供应渠道由上述4 部分构成，则站点m 的第j 项备件供应渠道均值为

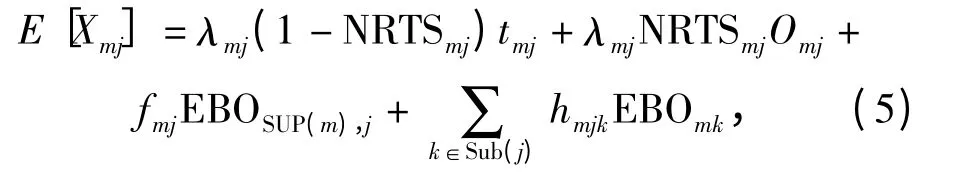
式中:SUP(m)表示直接对m 进行备件供应的上级保障站点;Sub(j)表示j 的分组件集合。

当站点m 向上级n(n∈SUP(m))申领备件时，上级出现备件短缺所造成对m 补给延误概率服从二项分布［14］。因此，根据(5)式可得出备件供应渠道方差为

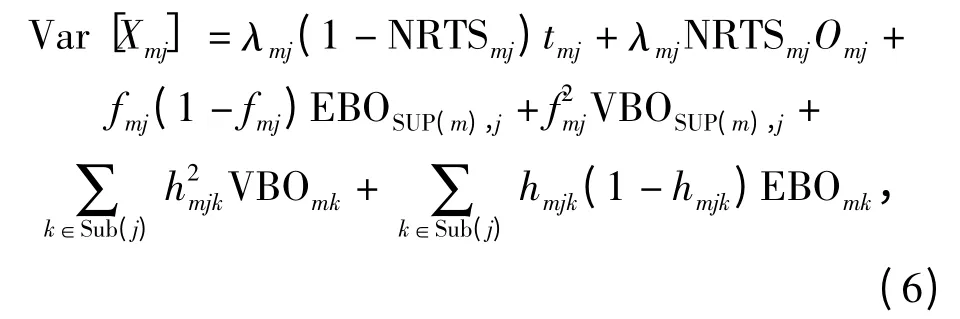
式中:EBOmj为备件期望短缺数;VBOmj为备件短缺数方差，可通过(5)式和(6)式计算得到的E［Xmj］和Var［Xmj］确定。当差均比Var［Xmj］/E［Xmj］=1时，备件供应渠道概率分布函数p(Xmj)用泊松分布计算;当Var［Xmj］/E［Xmj］＞1 时，用负二项分布近似计算［15］。当Var［Xmj］/E［Xmj］＜1 时，用二项分布对p(Xmj)作近似估计。

2 基于可用度的备件配置优化

装备可用度是衡量备件维修供应效能的重要指标，是指任意时刻，装备处于可工作或可使用状态的程度，使用站点m 的所有Nm个装备的期望可用度为

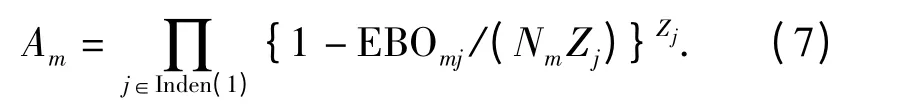
而整个保障体系的所有装备平均可用度为

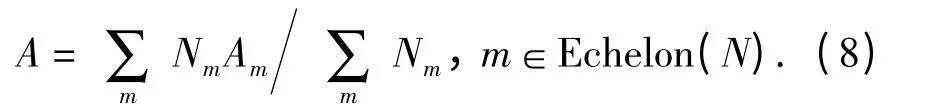
备件初始配置优化是在保证装备可用度指标的前提下，使整个保障体系的备件费用最低。所建优化模型如下:

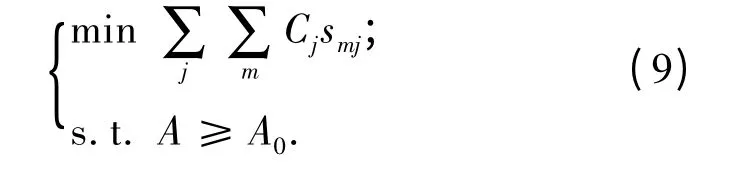
式中Cj表示第j 项备件的单价。对(7)式等号两端取对数，可将系统可用度指标转化为备件短缺数之和来近似处理，即

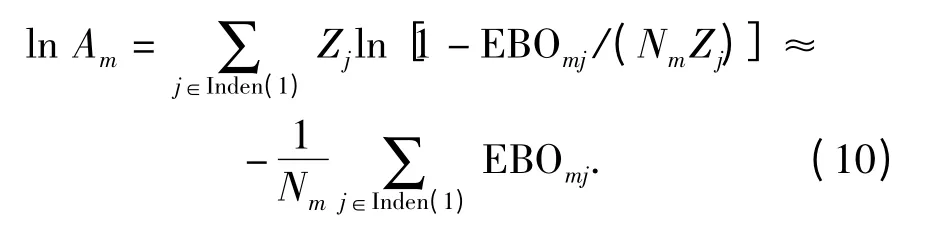
采用传统边际优化算法进行求解时，首先，初始化备件库存量，计算每一轮迭代过程中的边际效应值

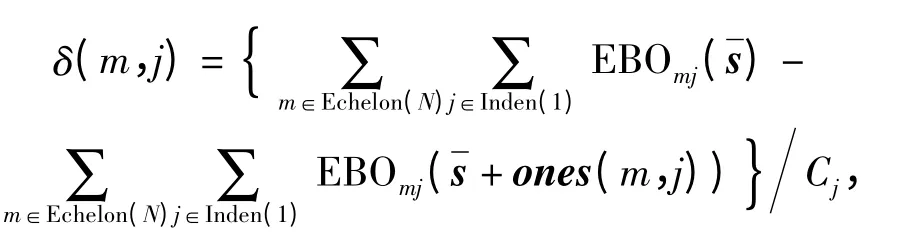
3 边际优化算法性能分析

边际优化算法在迭代过程中的最优费效曲线如图1所示，若设定指标A0=0.9，则曲线上所对应的大于A0的下一个点s*即为最优库存点，根据费效曲线，能够便于决策人员对设定指标和库存结果进行分析和调整。

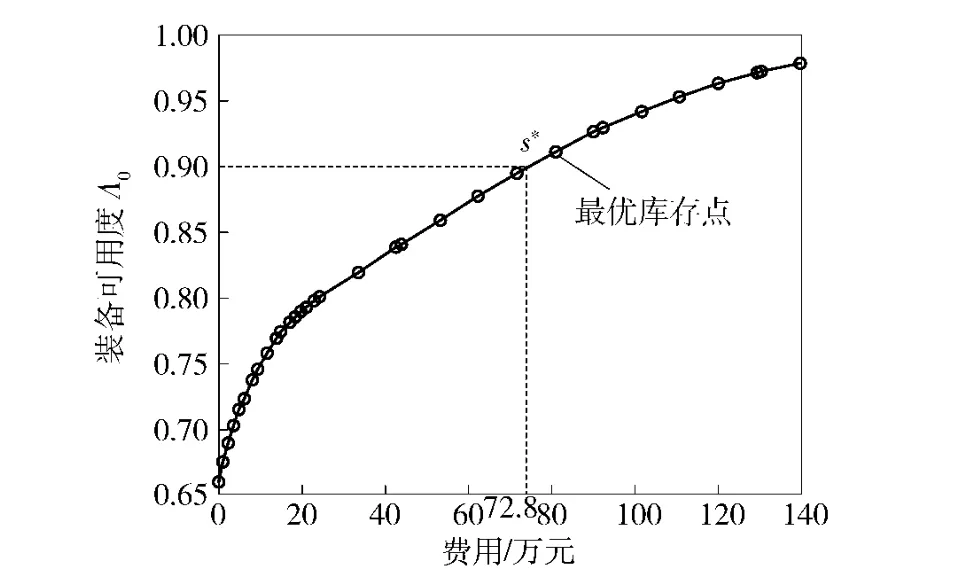
图1 边际优化算法的最优费效曲线Fig.1 The optimal curve of availability vs cost for marginal algorithm

该算法的不足之处主要体现在算法的搜索效率方面。如，设保障体系中的站点数量为m，装备系统中的备件类型数量为n，模型决策变量输出结果为一个关于各站点备件库存量集合的m ×n 矩阵

式中sij表示第i 个站点的第j 项备件配置量。首先进行变量初始化，令sm×n=［0］，分别对sm×n中的每一个元素加1，并计算其所对应的边际效应值δ(sij)(i∈［1，m］，j∈［1，n］).将最大值maxδ(sij)所对应的sij加1.确定下一个优化点时需要在当前变量矩阵sm×n的基础上进行分析，直到满足设定的指标为止。每确定一个最优点时，算法需要迭代次数为m·n，如果矩阵中的备件库存量之和sum(sm×n)=s，则算法在整个优化计算过程中需要迭代的次数为m·n·s.

4 改进的分层边际优化算法

4.1 优化算法设计

在传统边际优化算法的基础上，通过引入分层的思想对算法进行改进，以提高搜索效率。改进的算法步骤为:

1)根据装备可用度指标确定其所属的各项LRUj初始可用度A0j;

由于装备系统的可用度取决于其所属的LRU可用度大小，对于组成上具有串联结构的系统，可用度A 可表示为其所属的各项LRUj可用度之积:

若设定系统可用度指标为A0，并认为各项LRU具有相同的关键度(模型中暂不考虑非关键部件)，即任何一项LRU 失效都会导致系统停机。根据(11)式可知:要保证A≥A0，LRUj的可用度必须至少满足A0j≥A0.

2)采用边际优化算法分别对每项LRU 及其SRU 进行优化计算;

3)进行算法迭代，在满足每项LRUj的可用度指标A0j情况下，得到关于LRUj的若干条可用度-费用曲线;

4)计算当前每项LRUj费效曲线上点的斜率

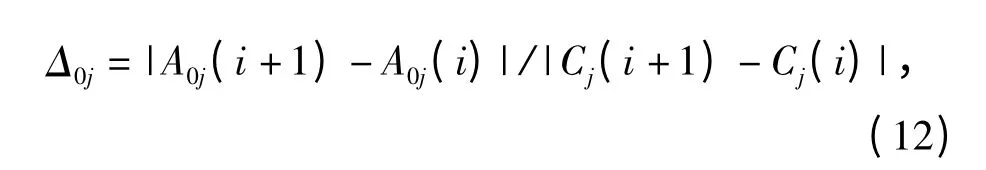
式中:|A0j(i +1)-A0j(i)|表示曲线上相邻点之间的可用度之差;|Cj(i +1)-Cj(i)|表示费用之差。若每项Δ0j的值近似相等并且LRUj的可用度之积满足∏Aj≥A0，则算法结束，得到最优备件方案;否则在当前备件方案的基础上，继续进行迭代计算，直到满足指标为止。算法流程如图2所示。

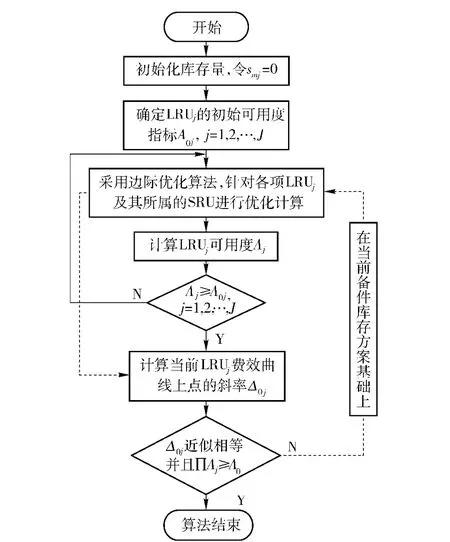
图2 分层边际优化算法流程Fig.2 The optimization flow of layered marginal algorithm

4.2 优化效率分析

证明:设第j 项LRU 及其所属的分部数量之和为nj，保障体系内的站点数量为m，每确定一个最优点时需要迭代m·nj次，若方案结果中LRUj及其SRUi的数量之和为sj，则需要迭代m·nj·sj次才能使LRUj满足指标A0j.完成系统的优化计算，基于分层的边际算法的迭代次数为

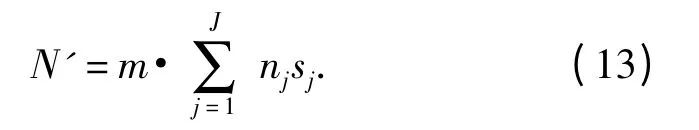
根据上述定义，系统中备件总数为n1+n2+…+nJ，优化结果中所有备件库存量之和为s1+s2+…+sJ，采用传统的边际优化算法进行计算时，需要迭代的次数为

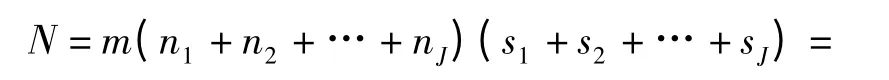
对于∀nj，sj，并且nj≥0，sj≥0，下列不等式恒成立

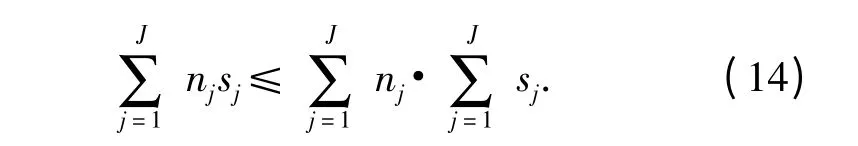
对于∀nj，sj不全为0 时，有N' ＜N.因此，改进的分层边际优化算法迭代次数要小于传统边际优化算法，从而具有更高的运算效率，证毕。

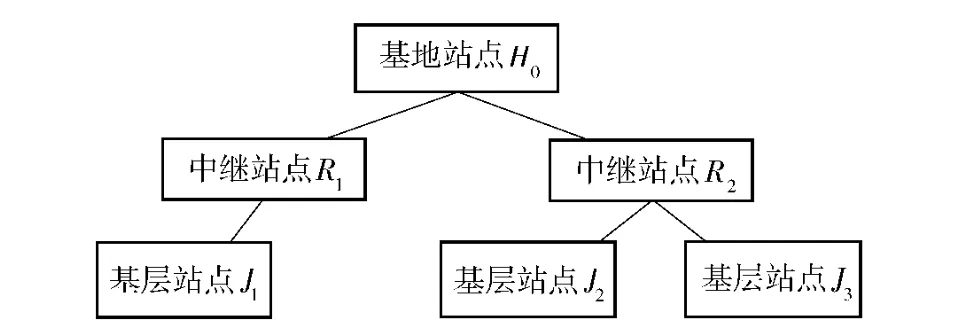
图3 保障体系的组织结构Fig.3 The framework and relation of support system

5 算例

由基地站点(H0)、中继站点(R1、R2)和基层站点(J1、J2、J3)构成的三级保障体系中，其组织结构如图3所示。装备部署在基层站点(J1、J2、J3)，配置数量Nm分别为18，12，15.需对各站点的备件初始库存配置量进行合理地规划，使保障体系内的装备可用度指标A0≥0.95，装备备件清单及其相关参数如表1所示。

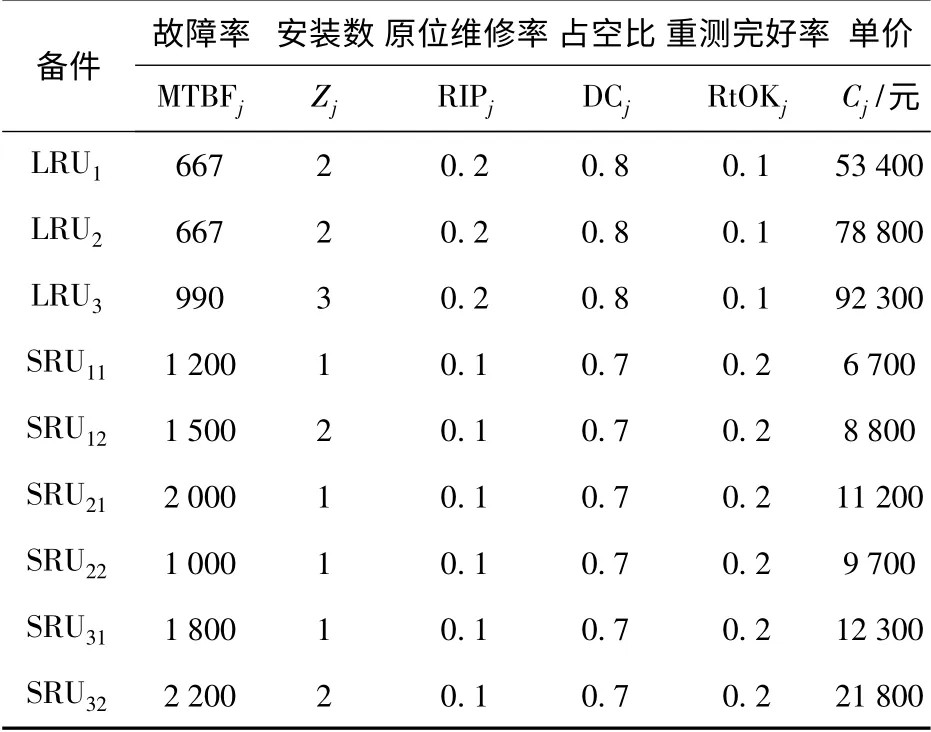
表1 装备备件清单及相关参数Tab.1 The spare parts’bill and the correlative parameters

根据改进的分层边际优化算法，可以得到关于LRU 的最优费效变化曲线，如图4～图6所示。计算各项LRU 费效曲线上大于0.95 的各点所对应的斜率，选择斜率近似相等的点并且使各项LRU 可用度之积大于等于0.95，最终得到最优库存点。所选择的LRU 最优方案点对应的可用度分别为A1=0.990 1、A2=0.980 4、A3=0.979 2.通过LRU 费效曲线合成得到装备系统的费效曲线如图7所示。

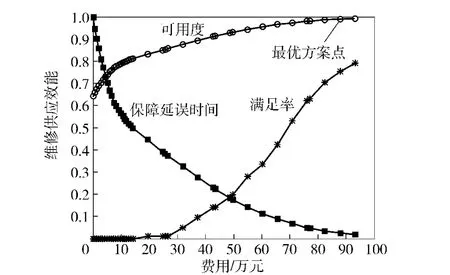
图4 LRU1 的最优费效变化曲线Fig.4 The optimal curves of effectiveness vs.cost for LRU1

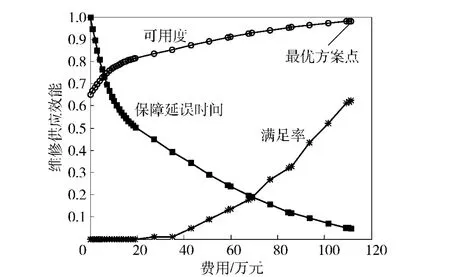
图5 LRU2 的最优费效变化曲线Fig.5 The optimal curves of effectiveness vs.cost for LRU2

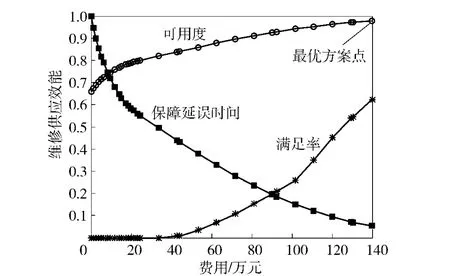
图6 LRU3 的最优费效变化曲线Fig.6 The optimal curves of effectiveness vs.cost for LRU3

最优配置方案如表2所示，在该方案下，整个保障体系的装备可用度A=0.950 42、备件满足率EFR=0.665 57、保障延误时间td=33.146 h、总费用C =337.98 万元。

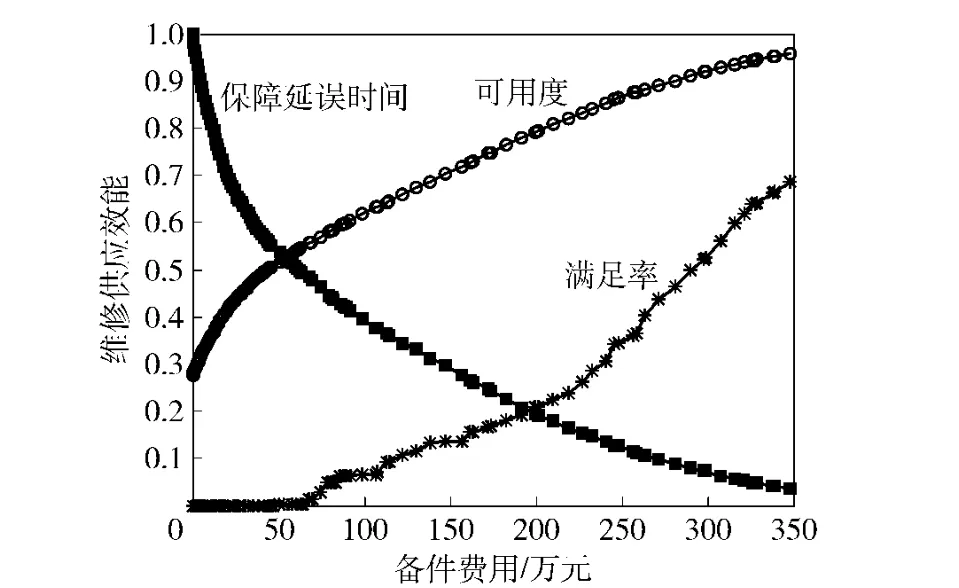
图7 装备系统的最优费效变化曲线Fig.7 The optimal curves of effectiveness vs.cost for system

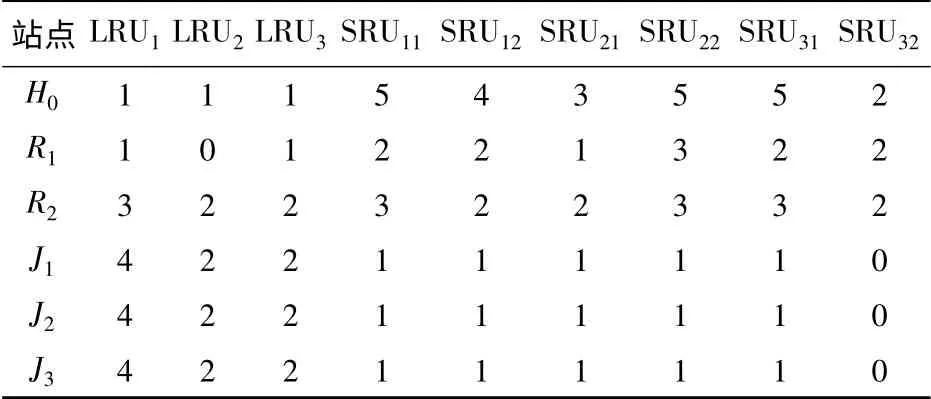
表2 备件的初始最优配置方案Tab.2 The optimal initial configuration project of items

将3 种不同算法的计算结果和优化时间进行比较，如表3所示，可得到各算法的特性和适用范围如下:

1)边际优化算法:操作简单、结果精度高，但优化效率较低。因此，该算法适合于针对备件层次结构简单、备件数量较少的优化问题。

2)改进的分层边际优化算法:搜索效率高、不仅能够得到系统单元级的费效曲线，通过曲线合成还能够得到系统级的费效曲线，可以对各单元影响因素的敏感性进行分析，便于对方案进行调整，但该算法的程序设计上相对复杂。因此，该算法适合于针对保障组织体系庞大、备件层次结构复杂、备件数量较多的优化问题。

3)人工免疫算法:搜索效率较高，能够将多指标优化问题通过抗体亲和度函数的构造而转化为单目标优化问题，缺点是算法稳定性差。此外，程序设计时需要选择合理的指标权系数和惩罚因子，否则会造成结果偏差。因此，该算法适合于针对备件层次结构复杂、数量规模大，具有多个约束目标的备件优化问题。

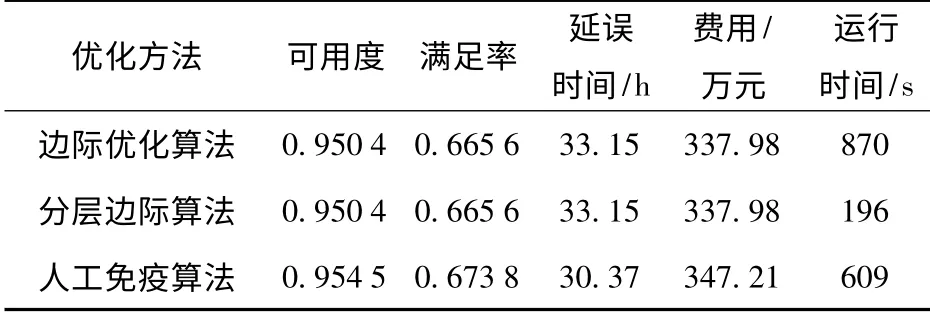
表3 不同算法的计算结果及运行时间Tab.3 The calculation result and time for different algorithms

6 结论

本文针对多级保障模式下的备件配置优化问题;提出一种改进的分层边际优化算法。通过算例中的数值结果可知:分层边际优化算法能够在保证优化结果完全一致的前提下，提高算法的优化效率，以本文算例为例，分层边际优化算法的运行时间为196 s，相比传统边际优化算法(870 s)，其运行时间提高了近3 倍，当系统中LRU 类型的数量较多时，这一优势更为突出。文中所提出的算法能够为复杂保障系统的备件配置优化节省大量的计算时间，工程上具有一定的实用性，为备件库存配置的优化方法提供一种新的思路。

文中在建立基于装备可用度的备件优化配置模型时，仅考虑了串联结构系统，因而需要根据实际需求对该问题作进一步深入研究。

References)

［1］ 周伟，郭波，张涛.两级供应关系装备常用备件初始配置模型［J］.系统工程与电子技术，2011，33(1):89 -93.ZHOU Wei，GUO Bo，ZHANG Tao.Initial configuration model for common equipment parts based on two-class supply relationship［J］.Systems Engineering and Electronics，2011，33(1):89 -93.(in Chinese)

［2］ Sherbrooke C C.Vari-metric:improved approximations for multiindenture multi-echelon availability models［J］.Operations Research，1986，(34):311 -319.

［3］ Lee H L.A multi-echelon inventory model for repairable items with emergency lateral transshipments［J］.Management Science，1987，33(10):1302 -1316.

［4］ Al-Rifai M H，Rossetti M D.An efficient heuristic optimization algorithm for a two-echelon (R，Q)inventory system［J］.International Journal of Production Economics，2007，(109):195 -213.

［5］ 阮旻智，李庆民，彭英武，等.任意结构系统的备件满足率模型及优化方法［J］.系统工程与电子技术，2011，32(8):1799-1803.RUAN Min-zhi，LI Qing-min，PENG Ying-wu，et al.Model of spare parts fill rate for system of various structures and optimization method［J］.Systems Engineering and Electronics，2011，32(8):1799 -1803.(in Chinese)

［6］ Kilpi J，Toyli J，Vepsalainen A.Cooperative strategies for the availability service of repairable aircraft components［J］.International Journal of Production Economics，2009，117(2):360 -370.

［7］ Archibald T W，Black D，Glazebrook K D.An index heuristic for transshipment decisions in multi-location inventory systems based on a pairwise decomposition［J］.European Journal of Operational Research，2009，192(3):69 -78.

［8］ Wu M C，Hsu Y K.Design of BOM configuration for reducing spare parts logistic costs［J］.Expert Systems with Applications，2008，34(1):2417 -2423.

［9］ Saranga H，Kumar U D.Optimization of aircraft maintenance support infrastructure using genetic algorithms-level of repair analysis［J］.Ann Oper Res，2006，143(1):91 -106.

［10］ 阮旻智，李庆民，王红军，等.人工免疫粒子群算法在系统可靠性优化中的应用［J］.控制理论与应用，2010，27(9):1253 -1258.RUAN Min-zhi，LI Qing-min，WANG Hong-jun，et al.Application of artificial immune particle swarm optimization algorithm to system reliability optimization［J］.Control Theory ＆ Application，2010，27(9):1253 -1258.(in Chinese)

［11］ Lee J Y，Schwarz L B.Leadtime management in a periodic-review inventory system:a state-dependent base-stock policy［J］.European Journal of Operational Research，2009，199:122 -129.

［12］ Sleptchenko A，van der Heijden M C，van Harten A.Effects of finite repair capacity in multi-echelon，multi-indenture service part supply systems［J］.International Journal of Production Economics，2002，79:209 -230.

［13］ 阮旻智，李庆民，彭英武，等.串件拼修对策下多级维修供应的装备系统可用度评价［J］.航空学报，2012，33(4):658-665.RUAN Min-zhi，LI Qing-min，PENG Ying-wu，et al.Evaluation of equipment system availability for multi-echelon maintenance supply with cannibalization［J］.Acta Aeronautica et Astronautica Sinica，2012，33(4):658 -665.(in Chinese)

［14］ Sherbrooke C C.Optimal inventory modeling of system:multiechelon techniques［M］.2nd ed.Boston:Artech House，2004.

［15］ 王乃超，康锐，程海龙.基于马尔科夫过程的备件库存动态特性分析［J］.兵工学报，2009，30(7):984 -988.WANG Nai-chao，KANG Rui，CHENG Hai-long.Study on the dynamic characteristics of spare inventory based on Markov process［J］.Acta Armanentarii，2009，30(7):984 -988.(in Chinese)

［16］ 阮旻智，李庆民，刘天华.编队防空火力分配建模及其优化方法研究［J］.兵工学报，2010，31(11):1525 -1529.RUAN Min-zhi，LI Qing-min，LIU Tian-hua.Modeling and optimization on fleet antiaircraft firepower allocation［J］.Acta Armanentarii，2010，31(11):1525 -1529.(in Chinese)