单水听器被动测距的信赖域最优化方法

刘俊星，章新华，綦敦浩，张本辉

(海军大连舰艇学院 水声信息研究中心，辽宁 大连116018)

0 引言

水雷是海军海上防御与对敌封锁作战的有战略作用的水中常规兵器，具有隐蔽性好、打击突然、威胁时间长、敌清除困难、效费比高的特点。在水雷引信中，声引信有着广泛的应用。水雷对目标进行攻击时需要估计目标距离，一旦目标进入到水雷的作用区域，声引信工作，引爆水雷摧毁目标。单个水雷利用单个水听器接收目标信号，提取有用信息，实现对目标运动状态的跟踪及预测，计算引爆水雷的最佳时间，所以单水听器被动测距是水雷发挥其作战性能的关键技术。

文献［1 -2］研究了多普勒最接近法，并将其运用于被动定向浮标目标定位，实现了单枚被动定向浮标对目标的发现、定位、追踪，但只能对匀速直线运动的目标有效，同时，必须准确测出目标过航路捷径点的时间及特征频率。文献［3］改进了多普勒最接近法，增强了测距实时性，但测距存在理论误差。

本文在多普勒最接近法的基础上，研究了基于最优化信赖域算法的单水听器被动测距方法。目的是解决单水听器对运动目标的实时测距，并预测目标距离等问题，以便更好应用于水雷声引信。

1 多普勒最接近方法

目前单个水听器实现对运动目标的测距主要是利用运动目标的多普勒频移信息，具体实现流程图如图1所示。

图1 测距流程图Fig.1 Ranging flow chart

多普勒最接近法是比较常用且研究较多的方法，如图2所示，当目标以速度v 从左向右运动。

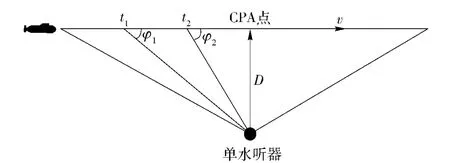
图2 水听器目标位置图Fig.2 The location of hydrophone and target

根据多普勒频移理论，水听器检测到的目标特征线谱有从高到低的变化过程。其中D 为目标航路捷径点的距离(即CPA 点的距离)［1］。

根据多普勒频移公式，水听器检测到目标的线谱频率为

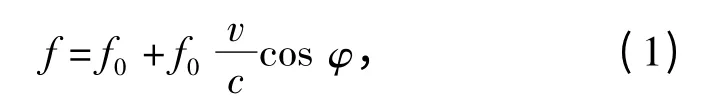
式中:f 为测量的目标频率;f0为目标的特征频率;v为目标的运动速度;φ 为目标航向到水听器连线的夹角;c 为声音传播速度。在t1、t2时刻分别测量线谱频率F1、F2.当目标由接近水听器到离开水听器，通过记录线谱的变化，如图3所示，根据线谱变化过程，求得线谱曲线的拐点(CPA 点)位置，从而可以得到目标到达CPA 点的时间TCPA及频率fCPA［2］.记:

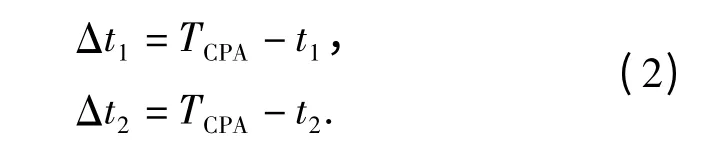
由(1)式可知:

图3 理想的观测频率时间曲线Fig.3 The ideal frequency curve graph

对(4)式、(5)式两边平方、化简，并记:

t1，t2，y1，y2均已知，求解此方程组，即可求得v，D［4］.

多普勒最接近方法利用任意两个时刻的目标多普勒信息，加上目标过CPA 点的时刻及频率，可以估计出目标的绝对速度和最接近距离，但不能实时给出目标的距离［3］。

2 改进多普勒测距法［5］

如图4所示，以水听器为坐标原点建立直角坐标系，设目标的初始位置为(x0，y0)，从目标初始位置开始计时，如果目标匀速直线运动，则有

代入(1)式得

如果目标是匀加速直线运动，设加速度为a，初速度为v0，则有

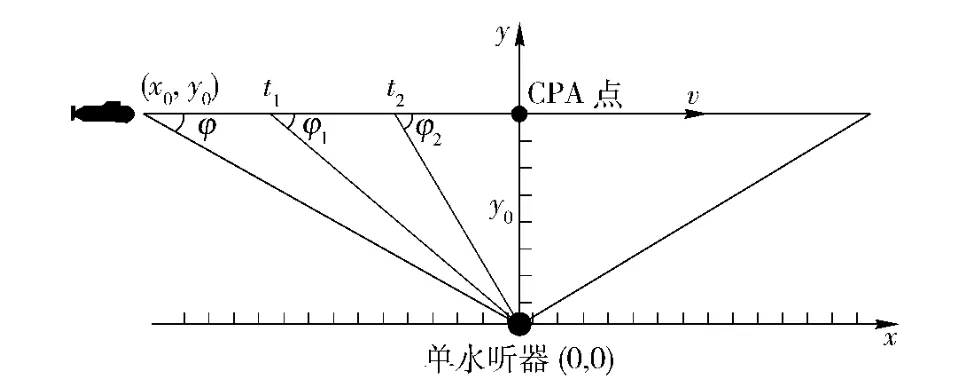
图4 水听器目标直角坐标位置图Fig.4 The location of hydrophone and target in rectangular coordinate

代入(1)式得

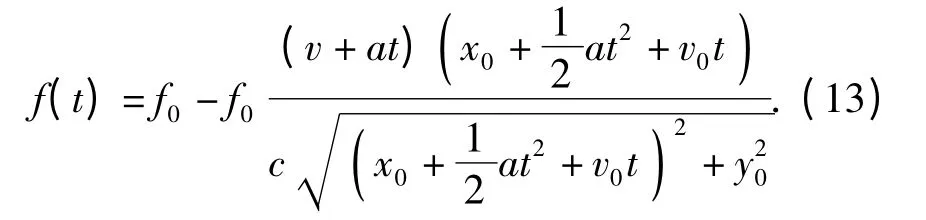
(11)式、(13)式为目标时间与频率的关系表达式，理论上来说，只要观测几个时间点的频率值，就能通过解方程组的方法求得运动参数，但这种方法要求观测频率值必须是无误差的，不符合实际应用情况。本文只要观测一段时间内的目标频率fd(t)，采用曲线拟合的优化方法估计出目标未知参数进而计算水听器与目标的距离:

或

(14)式、(15)式中当t 等于观测时间就是对当前目标距离的估计，t 大于观测时间就是对目标距离的预测。所以任何时刻都能根据记录的频率估计目标距离，体现了实时性。但由于每次测距都需要优化，计算量较大，所以本文的实时性是建立在具有高速计算性能的硬件基础上的。

2.1 信赖域最优化方法

最优化问题就是求一个多元函数在某个给定集合上的极值，对于非线性优化参数估计的算法主要有Gauss-Newton 法、Levenberg-Marquardt 法及trustregion(信赖域)法［7］。本文选用信赖域算法，信赖域算法是求解无约束优化问题的一类有效算法［5］:

其基本思想是设xk是第k 次迭代点。记fk=f(xk)，gk=Δf(xk)，d = x - xk，Bk是Hesse 阵Δ2f(xk)的第k 次近似，则f(x)在xk的泰勒二阶展开为

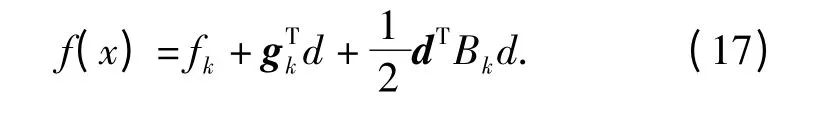
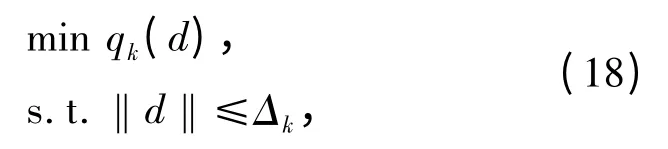
式中:Δk是信赖域半径;‖·‖是任何一种向量范数，通常取2 范数或∞范数，设子问题的最优解为dk，定义Δfk为f 在第k 步的实际下降量，

Δqk为对应预测下降量，

再定义它们的比值为

一般地，有Δqk＞0，因此，若rk＜0 则Δfk＜0，xk+dk不能作为下一个迭代点，需要缩小信赖域半径重新求解子问题。若rk比较接近1，说明二次模型与目标函数在信赖域范围内有很好的近似，此时xk∶=xk+dk可以作为新的迭代点，同时下一次迭代时可以增大信赖域半径。对于其他情况，信赖域半径可以保持不变［6］。将该方法应用于本文的被动测距，令(16)式中:

式中x=(f0，v，x0，y0)T，选取合适的搜索初值及信赖域半径，找到使目标函数f(x)最小的点便是所求的估计值［5］。

2.2 信赖域算法［8］

信赖域算法实现步骤如下:

步骤0 选取控制迭代的参数值，初始点x1∈Rn，0≤η1＜η2＜1，0 ＜γ1＜1 ＜γ2，0≤ε≪1.取定＞0 为信赖域半径的上限，初始信赖域半径Δ1∈(0，］，令k∶=1.

步骤1 计算gk=Δf(xk)，若‖gk‖≤ε，停止迭代。

步骤2 求解子问题(18)式的解dk.

步骤3 按(21)式计算rk值。

步骤4 校正信赖域半径:

步骤5 若rk＞η1，则令xk+1∶=xk+dk，更新矩阵Bk到Bk+1，令k∶=k+1，转步骤1;否则xk+1∶=xk，令k∶=k+1，转步骤2.

3 仿真及结论

3.1 仿真

针对新方法进行计算机仿真，使用Matlab 作为仿真计算软件。利用Matlab 软件提供的lsqcurvefit 优化工具实现［9］，该工具的调用格式为［x，residual］=lsqcurvefit(myfun，x1，xdata，ydata，lb，ub)，式中x 为求取的估计参数向量，residual 为对fd(ti)拟合后的残差序列数据Δf(ti)=f(ti，x)-fd(ti)，xdata、ydata 为观测数据ti、fd(ti)(i=1，2，…，n)，myfun 为由(11)式或(13)式所描述的非线性函数表达式，x1、lb、ub 分别为搜索初值和上下限。系统默认算法为信赖域法。迭代参数取值如下:Δ1=

仿真条件如下:目标中心频率f0=1 000 Hz，目标匀速运动速度为v =8 m/s，目标初始位置坐标(x0，y0)=(-800 m，100 m)，即航路捷径点距离为100 m.水文环境为典型的浅海环境，弱负梯度，水中声音传播速度c=1 500 m/s，声波按直线传播，不考虑传播能量衰减，水声信道等的影响，水听器静止，频率测量周期为1 s.测量目标由起始位置到CPA 点之前的频率，即观测时间为100 s，设测量频率附加0.2 Hz 的高斯白噪声。图5为信号整个过程的LOFAR 历程图。根据实际情况，设搜索初始值x1 =［fd(tn)，5，-500，200］，最大值ub =［fd(tn)+10，50，-10，10 000］，最小值lb =［fd(tn)-10，0，-4 000，1］.

仿真计算结果为:经过17 次迭代后得估计目标中心频率^f0= 999.896 9 Hz，估计目标速度^v=8.163 3 m/s，估计目标初始位置坐标(-819.862 9 m，104.471 3 m).然后通过(14)式对目标距离估计及预测，图6为仿真图。

假设目标为匀加速直线运动模型，则设目标加速度a=0.2 m/s2，初速度v0=3 m/s，测量目标由起始位置到CPA 点之前的频率，其余仿真条件不变。仿真结果如下:目标中心频率^f0=998.8 Hz，加速度=0.200 5 m/s2，初速度=2.391 m/s，目标初始位置坐标(-753.2 m，97.31 m)，仿真图如下:

图5 信号LOFAR 历程图Fig.5 The history plot of signal LOFAR

图6 匀速运动目标实时测距及预测距离仿真图Fig.6 The simulation diagram of real-time ranging and forecasting distance of uniform motion target

图7 匀加速运动目标实时测距及预测距离仿真图Fig.7 The simulation diagram of real-time ranging and forecasting distance of uniformly accelerated motion target

由以上计算结果可知该算法的正确性，下面着重研究观测时间、频率测量周期、目标初始位置及目标运动速度对测距结果的影响。在仿真分析目标运动参数对测距性能的影响时，采用作50 次Monte Carlo 的方法，给出了距离真值、估计距离均值及均方差，距离真值和估计距离均值可以表征距离估计的无偏性，估计距离的均方差可以表征距离估计的有效性。

改变观测时间，其余仿真条件不变，以估计目标当前时刻距离的真实值、估计距离平均值、均方差及估计航路捷径点的距离(实际距离是100 m)作为比较测距性能优劣的标准。结果见表1.

表1 不同观测时间测距仿真分析Tab.1 The simulation analysis of different observation time

有时被动目标测距会给出测距过程的累积误差，累积误差是在指每个时刻的估计误差将影响下个时刻参数估计的精度，并具有传播性形成积累误差，且累积误差会随着时间增加［10］。本文采用的是曲线拟合的参数估计方法，每个时刻的参数估计都是利用之前所有观测的数据进行拟合估计，与前一时刻的估计值不存在递推关系，且由上表可知随着时间增加，误差越小，所以该算法完全消除了累积误差。

再比较目标不同的运动速度对测距结果的影响，改变目标运动速度，观测时间为目标从起始位置开始运动到CPA 点为止，仿真重复50 次，其余仿真条件不变，以估计目标在CPA 点的距离真实值、估计距离平均值及均方差作为比较测距性能优劣的标准。结果如表2所示。

表2 不同目标速度测距仿真分析Tab.2 The simulation analysis of different target speed

改变频率测量周期，观测时间为目标从起始位置开始运动到CPA 点为止，其余仿真条件不变，仿真重复50 次，以估计目标在CPA 点的距离真实值、估计距离平均值及均方差作为比较测距性能优劣的标准。结果如表3所示。

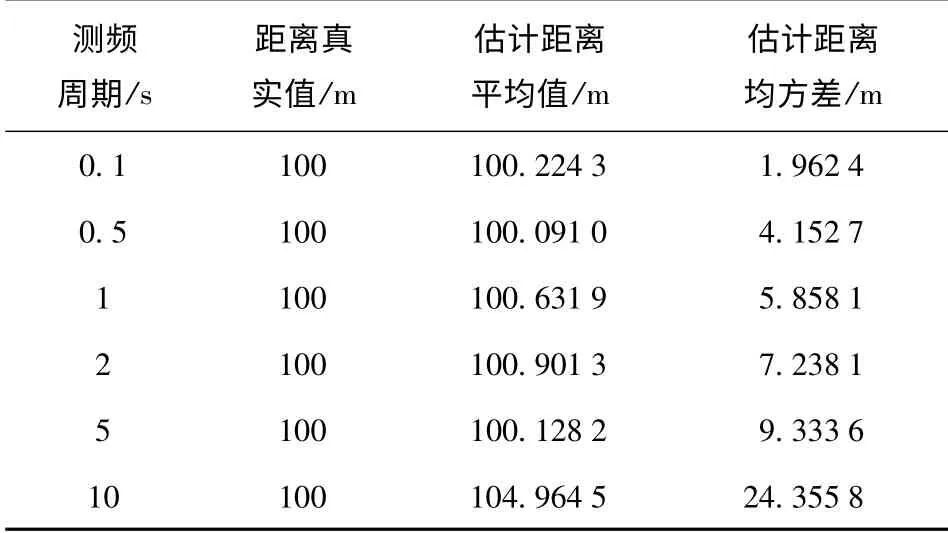
表3 不同频率测量周期测距仿真分析Tab.3 The simulation analysis of different frequency measurement period

3.2 仿真结论

由以上仿真结果可以得出以下结论:1)由图6、图7可知，目标运动至CPA 点附近，测距误差变小，离CPA 点越远，测距误差越大，因为CPA 点附近的多普勒变化率最大;2)由表1可以看出，目标运动到CPA 点之前就可以估计目标运动参数，同时观测时间对测距误差影响明显，观测时间越长，误差越小，因为观测时间越长，数据点就越多，观测到得多普勒频移量就越大;3)由表2可见，目标运动速度越快，测距误差越小，因为速度越快，多普勒频移就越大;4)理论上，频率测量周期越短，相同的观测时间，数据点就越多，频率附加0.2 Hz 的高斯白噪声对测距结果影响也就越小，这符合表3给出的结果，但实际工程应用上，测频周期越短，频率分辨率就越低，带来的误差也越大。

4 结束语

基于最优化方法的单元被动测距法，充分利用单个水听器接收的多普勒信息，运用最优化方法的信赖域算法估计目标运动参数。该方法可以在航路捷径点之前对目标实现实时探测，不仅能直接获得目标当前运动状态及预测目标状态，还适用于目标匀加速运动模型。将其运用于水雷声引信上，将更好地发挥水雷作战性能。

但该方法对频率测量精度依赖性很大，如何解决频率测量周期与频率分辨率的矛盾是下一步需要研究的内容。而且，本文研究的测距方法都是已知了目标是匀速直线运动或匀加速直线运动，在实际作战中，不可能事先完全知道目标运动规律，目标也不可能完全遵循匀速直线运动或匀加速直线运动，所以能否根据观测量来判断目标的运动规律也是需要进一步研究的。

References)

［1］ 陶林伟，王英民，王成，等.声纳浮标多普勒最接近法的一种新算法［J］.系统仿真学报，2008，20(23):6353 -6355.TAO Lin-wei，WANG Ying-min，WANG Cheng，et al.New algorithm for sonobuoy Doppler-CPA［J］.Journal of System Simulation，2008，20(23):6353 -6355.(in Chinese)

［2］ 陶林伟，王英民.一种新的单枚被动定向浮标目标定位方法［J］.兵工学报，2011，32(3):365 -369.TAO Lin-wei，WANG Ying-min.A target location algorithm based on single direction finding and ranging sonobuoy［J］.Acta Armamentarii，2011，32(3):365 -369.(in Chinese)

［3］ 郁涛.对水下目标的多普勒直接定位［J］.中国电子科学研究院学报，2011，6(3):328 -330.YU Tao.Doppler direct location for underwater target［J］.Journal of CAEIT，2011，6(3):328 -330.(in Chinese)

［4］ TAO Lin-wei，WANG Ying-min.A new single DIFAR sonobuoy target location algorithm［J］.Journal of China Ordnance，2011，7(3):153 -157.

［5］ 王永杰.利用引信多普勒频率估计导弹脱靶量方法研究［J］.系统工程与电子技术，2005，27(11):1914 -1931.WANG Yong-jie.Research on estimating missile miss distance using fuze Doppler spectrum［J］.Systems Engineering and Electronics，2005，27(11):1914 -1931.(in Chinese)

［6］ 孙文瑜，徐成贤，朱德通.最优化方法［M］.第二版.北京:高等教育出版社，2010.SUN Wen-yu，XU Cheng-xian，ZHU De-tong.Optimization method［M］.2nd.Beijing:Higher Education Press，2010.(in Chinese)

［7］ 王德人.非线性方程组解法与最优化方法［M］.北京:人民教育出版社，1979.WANG De-ren.Solving nonlinear equations and optimization method［M］.Beijing:People's Education Press，1979.(in Chinese)

［8］ 马昌凤.最优化方法及其Matlab 程序设计［M］.北京:科学出版社，2010.MA Chang-feng.Optimization method and Matlab program design［M］.Beijing:Science Press，2010.(in Chinese)

［9］ 魏巍.Matlab 应用数学工具箱手册［M］.北京:国防工业出版社，2004.WEI Wei.Matlab toolbox of applied mathematics handbook［M］.Beijing:National Defense Industry Press，2004.(in Chinese)

［10］ 嵇玮玮，刘中.递增式传感器节点定位方法的累积误差分析及其改进［J］.南京理工大学学报:自然科学版，2008，32(4):496 -501.JI Wei-wei，LIU Zhong.Accumulative error analysis of incremental node localization approach and its improvement in wireless sensor network［J］.Journal of Nanjing University of Science and Technology:Natural Science，2008，32(4):496-501.(in Chinese)