双兰杰文振子V型直线超声波电动机的设计与实验

乔 木，洪尚任

(华侨大学，福建厦门362021)

0 引 言

超声波电动机拥有许多传统电机无法比拟的优势，比如重量轻、无电磁干扰、机械结构简单、无需齿轮减速器、噪声低、高自锁力和高的位置精度等，使得超声波电动机在许多工业领域得到了广泛的应用。

本文提出了一款由双兰杰文振子组成的V型超声波直线电动机，详细介绍了电机的工作原理并且使用有限元分析的方法优化了电机的定子。

1 V型电机定子的结构和工作原理

1.1 V型电机定子的结构

由图1可知，电机的定子部分由摩擦材料、前盖板、压电陶瓷、螺母、支撑架和双头螺杆组成。

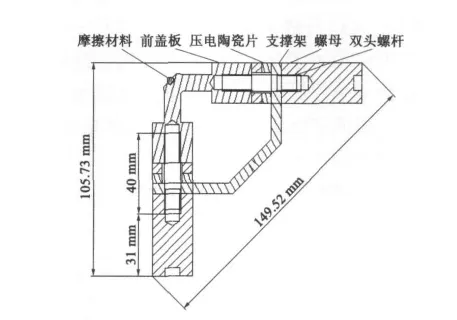
图1 V型电机定子结构

前盖板采用的是阶梯型变幅杆，目的是将压电陶瓷产生的振动能放大。这里使用密度小、能够承受很大张拉应力的铝合金2AI1;定子尾部的螺母使用的是不锈钢304，它的特点是密度大、强度高，声速较铝合金材料小，有利于振动波最大限度地向前辐射，从而提高电机的效率。同时尾部使用重金属，还能够有效地缩短定子的尺寸;定子中部是两对面对面放置的圆环形压电陶瓷片，尺寸是Φ20 mm×Φ10 mm，其中正极接在两个压电陶瓷片中间，电极片使用的是普通薄铜片。为了消除压电陶瓷片和薄铜片之间空气间隙，并且提高定子组装效率，我们使用环氧树脂胶将压电陶瓷片和铜片粘成了一体。摩擦材料使用的是碳素工具钢T8。支撑架的厚度是5 mm，使用的材料是铝合金2AI1，它的作用是将两侧的兰杰文振子连接在一起，并且通过它将定子与外界固定起来。

1.2 电机的工作原理

使用ANSYS软件对定子进行固有模态计算。将支撑架的下表面作为位移约束。当给定子两侧接入相同频率、相同相位的高频电信号时，将激发出图2(b)所示的对称振动，此时定子驱动足法向运动;当定子两侧接入的电信号频率相同，相位相反时，将激发出图2(a)所示的非对称振动，此时定子驱动足切向运动。

图2 定子的工作模态

如果给定子左右两侧接入两个同频、相位差为90°的高频电信号时，调整输入电流的频率，直到能够同时激发出对称和非对称两个振动模态。这样，两个振动叠加的结果是，定子的驱动足上出现椭圆运动。当切换左右两侧的电信号，驱动足的椭圆运动将反向。

在ANSYS中所需要的各种材料参数和有限元划分的单元类型，如表1所示。

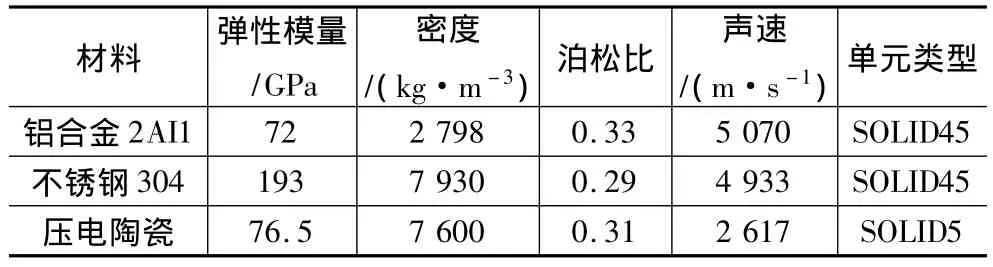
表1 材料参数表

2 使用ANSYS软件对定子进行优化

使用ANSYS软件对定子进行固有模态计算，由计算结果可知，定子是利用一阶纵振和二阶弯振工作的。最初设计的定子，其对称振动和非对称振动的固有频率差为826 Hz，而且伪振动(驱动足部分振动方向垂直于对称振动和非对称振动的工作面)的固有频率与非对称的固有频率差仅为950 Hz。所以需要对定子进行优化。优化的目标是对称振动和非对称振动的固有频率差控制在300 Hz左右，伪振动的固有频率要远离对称振动和非对称振动的固有频率。这里将螺母的长度作为调整参数，图3为螺母长度与定子固有频率的关系曲线。图4是定子伪振动的位移云图。

当后盖板长度为41 mm时，V型定子的非对称振动模态(24 734 Hz)和对称振动模态(25 021 Hz)的频率差是287 Hz，达到了优化要求。而此时的伪振动(22 982 Hz)也已经远离了两个工作模态。

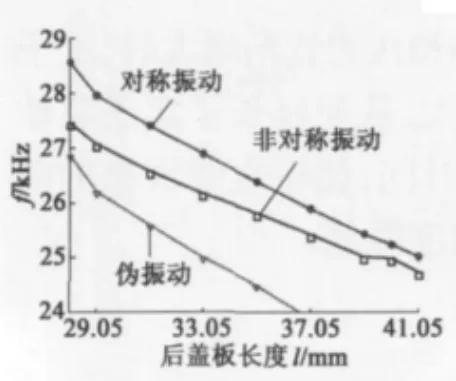
图3 螺母长度与定子固有频率的关系曲线

图4 伪振动位移云图(22 982 Hz)

通过图2可以看到，支撑架的变形量非常小，说明支撑架确实位于两个兰杰文振子的位移节面处。这样就可以最大限度地降低由于支撑架的变形而消耗的能量，提高了电机的输出效率。

3 V型电机的输出特性

图5是实验平台照片，直线滑轨的材料为45#钢，行程130 mm，移动部分的重量是100 g，定子两侧螺母的预紧力为7 N。

图5 实验平台

3.1 无负载速度－频率特性

当弹簧预压力F=11 N，电源输入电压峰－峰值680 V，相位差90°时，电机的无负载速度－频率特性曲线如图6所示。由图6可知，实验样机的谐振频率 f=22.9 kHz。当电源的激励频率逐渐远离谐振频率时，电机的输出速度逐渐降低。在预压力11 N，输入电压峰－峰值680 V，相位差为90°时，电机无负载的输出速度达到162.5 mm/s。输入频率22～24 kHz范围内变化时，电机速度都在40 mm/s以上。由此可以说明，电机可工作的频率范围很大，抗干扰能力较强。

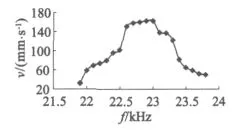
图6 电机无负载的速度－频率特性曲线

3.2 无负载速度－预压力特性

图7给出的是电机在驱动频率f=23.32 kHz，输入电压峰－峰值680 V，相位差为 90°时，无负载的情况下测得的速度－预压力曲线。

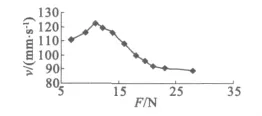
图7 无负载速度－预压力特性

由图7可以得知，预压力的大小对于电机的输出速度有很大的影响。当预压力F=11 N时，电机输出的速度最大。在较小的预压力下，定子驱动足与导轨之间的压力较小，即定子驱动足与直线滑轨之间的弹性变形量较小，使得定子驱动足与直线滑轨间的接触时间较短，所以直线滑轨的前进步幅较大，这时电机表现出的是速度比较快;当电机的预压力逐渐增大时，定子驱动足部分的弹性变形加大，从而延长了定子驱动足与直线滑轨之间的接触时间，使得直线滑轨的前进步幅减小，电机的输出速度降低。

3.3 无负载速度－电压特性

图8 无负载速度－电压特性

图8给出的是电机在给定谐振频率f=22.9 kHz，相 位 差 为90°，预压力 F=11 N时，测得的无负载速度－电压特性曲线。本次实验中，使用了四个不同电压峰 －峰值，分别为 600 V、680 V、780 V、880 V，通过图8可以发现，随着电压的增加，电机的输出速度不断提高。在谐振频率f=22.9 kHz，电压峰－峰值为880 V，相位差为90°，预压力F=11 N时，电机取得了本次实验的最大值，达到了206 mm/s。

3.4 有负载速度－频率特性

电机在实际使用过程中，一定是带有负载的。所以，电机在施加负载后的工作状态，对于电机实际的应用更加具有参考价值。

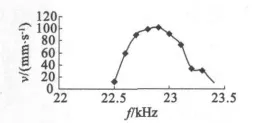
图9 有负载速度－频率特性

电机有负载速度－频率特性，如图9所示。在接入负载G=1.93 N后，为了增加定子驱动足与直线滑轨间的摩擦力，我们增加了预压力，实验中的预压力F=21 N。在实验过程中，调节不同的频率，直线滑轨的运动很平稳，没有噪声。电机在谐振频率f=22.9 kHz处，速度达到最大值为102 mm/s。与图6对比可知，接入负载G=1.93 N后，电机的可工作频率范围变小。

3.5 单侧兰杰文振子驱动时的速度－频率特性

当只有一侧的振子被激励时，由压电陶瓷产生的纵振波一部分传递到了驱动足，而另一部分纵振波则传向了另外一侧的振子，经过后盖板反射后再次到达驱动足。这列经过反射后的波便与激振源产生的振动波出现了相位差。这相当于另一侧的振子也被施加了一个同频率不同相位的振动信号。所以，在某一频率范围内，定子驱动足依然可以产生对称振动和非对称振动。两种振动叠加的结果，便是定子驱动足上的椭圆运动。

图10 单侧驱动速度－频率特性

图10是给定驱动电压峰 －峰值680 V，弹簧的预压力F=11 N时，无负载条件下，单个兰杰文振子的速度－频率特性。

3.6 电机输出力实验

实验测得电机最大输出力为10.5 N，单侧振子驱动时的最大输出为5 N。但是，同时发现当负载超过5 N时，由于需要增加预压力以提供足够大的摩擦力，电机在驱动负载的运行中，噪声开始加大。当负载达到10 N时，定子驱动足与导轨之间的磨损开始加剧，使得电机在运行中发出刺耳的噪声，并且直线滑轨的运行变得很不平稳，运动速度不均匀。这是由于定子驱动足与直线滑轨之间出现打滑现象引起的。这说明界面的摩擦系数不够大。本次试验驱动足与直线滑轨构成的摩擦副的摩擦系数约为0.2。如果要提高电机的输出力和寿命，还需要提高直线滑轨和定子之间摩擦副的摩擦系数。图11是输出力实验前后，直线滑轨表面的对比。

4 结 语

本文设计了一款V型超声波直线电动机，使用ANSYS软件计算了电机的对称模态和非对称模态频率，并对定子进行了优化。优化的结果是对称模态和非对称模态的频率差为287 Hz，使两者能够更好的简并。对电机做了比较详细的输出特性实验，实验表明该电机最大输出速度206 mm/s，最大输出力10.5 N。

［1］ Kurosawa M，Kodaira O.Transducer for high speed and large thrust ultrasonic linear motor using two sandwich － type vibrators［J］.IEEE Trans.on ultrasonics，ferrodectrics，and frequency control，998，45(5):1188 －1195.

［2］ Asumi K，Kurosawa M.Miniaturization of a V －shape Transducer Ultrasonic Motor.The Japan Society of Applied Physics，2009，44(07GM02):1－5.

［3］ 胡国良.Ansys11.0有限元分析入门与提高［M］.北京:国防工业出版社，2009.

［4］ 李朝东.直线型压电驻波超声电机的研究［D］.南京:南京航空航天大学，1998.

［5］ 林书玉.夹心式压电陶瓷功率超声换能器的优化设计［J］.压电与声光，2003，25(3):199 －202.

［6］ 戴雄杰.摩擦学基础［M］.上海:上海科学技术出版社，1989.