高速内嵌式永磁电动机转子机械强度分析

陈远扬，韩则胤，陈阳生

(1.浙江大学，浙江杭州310027;2.中国航天万源国际集团有限公司，北京100176)

0 引 言

内嵌式永磁电动机(以下简称IPM)采用转子冲片内嵌磁钢块且磁极表面对称分布的方式，不仅使电机反电势波形得到优化，而且有效地抑制了电机齿槽力矩和负载力矩扰动。由于电机存在dq轴不对称，凸极效应产生的附加磁阻转矩将进一步提高电机效率。由电机的磁路分析表明，经过磁保护的磁钢，其抗去磁能力增强，电机体积有效减小，功率密度得到大大提高。经过合理的机械设计，相比采用普通瓦形或者环形磁钢的电机，IPM电动机转子结构坚固可靠，无需额外绑扎等其它加固措施，加工工艺简单，更适合高速弱磁运行。因此，内嵌式永磁电动机转子结构具有结构简单、尺寸灵活多样且效率高、功率密度大等优点［1-3］。

常规的高速IPM电动机中，极靴由于远离旋转中心，将受到很大的离心力作用而产生严重的形变，而连接极靴的隔磁桥将承受极大的应力。为提高转子的机械强度，一般需要采取增加隔磁桥宽度(如图1所示)的措施来减小形变。但这使得电机漏磁大幅增加，电机性能下降。因此对于IPM电动机，转子强度和应力分析将是一个必要的设计环节。

图1 常用IPM转子结构和作用力方向示意图

本文以高速运行的IPM电动机为研究对象，分析了电磁力与离心力、永磁体吸引力三种力对于转子形变的影响。常规的电磁及结构有限元分析由于考虑上述三种类型的力的共同作用，涉及电磁场与结构场的切换，导致流程复杂，计算量大。本文提出了一种灵活高效的简化模型分析法，该方法利用电磁有限元网格剖分，来计算转子离心应力，具有流程简单、计算量小的特点。仿真和实验结果表明，该方法实用有效。

1 基于有限元的机械应力分析

一般情况下，IPM电动机具有Ⅰ型、V型两种常用的转子结构如图1所示。这两种IPM转子均通过隔磁桥饱和来限制漏磁通的大小以达到隔磁的目的。在V型IPM中为了降低隔磁桥受力以减小极靴形变，一般还会采用辅助隔磁桥(隔磁桥2)。

该两种IPM电动机转子的受力分析如图1所示，转子受力分析时，一般考虑以下三种力的作用，即离心力、定转子电磁力以及转子吸引力。其中离心力和定转子电磁力的方向相同，均径向向外，而永磁体和转子铁心之间的吸引力则垂直于永磁体边界径向向内。本文将分析上述三种力对于转子应力及形变的影响。

1.1 有限元分析模型

对于IPM电动机性能的分析，有限元是一种有效的分析手段。其中电磁有限元可以得到转子隔磁桥和极靴饱和的状况及电磁性能，而结构有限元可以分析隔磁桥部分的形变状况。基于强度分析中结构场与电磁场弱耦合性的特点，分析过程如下:先构建电机有限元节点与单元模型，接着对该电磁模型进行电磁力的计算和电磁性能的分析，最后将电磁模型分析的结果作为结构分析中结构场的边界条件，进行相应的应力计算及结构分析［4］。

由电磁模型的分析可知，根据电机的对称性，6极电机只需对1/3电机模型进行分析即可。定转子相对位置不同时，电磁力的分布是不同的。通过改变定转子的相对位置可以得到不同的旋转位置下的电磁分布情况。

电磁有限元分析主要得到两方面的结果:一是作为结构场边界条件的转子电磁力分布情况;二是电机的电磁性能，包括其反电动势和漏磁。结构有限元分析着重考虑的是转子的应力分布以及极靴部分的形变状况。

1.2 转子应力形变结果分析

由于磁钢和转子的接触并非理想接触，中间存在的间隙和黏胶等物质的磁导率远小于硅钢材料［5］，所以径向电磁力将垂直于转子外表面，不同位置的力的幅值会有变化(如图1所示)。转子冲片和永磁体之间的吸引力也基本上垂直于接触面。事实上，转子内部吸引力作为上述三种力中唯一方向不同的力，将起到消减离心力的作用。本文将分别进行三种情况下的有限元分析。

(1)独立转动 该状态下不考虑定转子内的磁性作用，转子单独在空气中转动，只计及离心力作用在转子上。

(2)空载状况 该状态下转子在无电流定子中旋转，与情况1相比，需额外考虑永磁体产生的电磁力。

(3)负载状况 该状态下定子绕组中施加了电流，转子在定子中旋转。与情况2相比，需多考虑定转子间的电磁力。后两种情况中唯一区别在于定子中是否有电流［6］。

当转速变化时，不同负载条件下6极Ⅰ型IPM转子隔磁桥部分的最大应力变化如图2(a)所示;相应的极靴的最大形变情况如图2(b)所示。

图2 6极Ⅰ型IPM转子隔磁桥部分最大应力及形变

由图2可知，三种情况的变化趋势是一致的。这是因为离心力和转速的平方成正比，满足关系Fc=f(ω2)，所以转子的离心力将随着转速的上升而增加，而永磁体与转子间的吸引力仅起到缓解离心应力的作用，其效果使得“空载”情况比“独立转子”时的应力和形变都小一些。“负载”时应力和形变又会略有增大，这主要是由于电枢反应产生与离心力同方向的电磁力造成的。

当转速变化时，离心力和电磁力分别产生机械应力和转子形变作用所占的比例如图3所示。当转速达到10 000 r/min时，机械应力作用和转子形变效果70%由离心应力提供，相比之下，电磁力的作用低得多。

图3 离心力和电磁力对最大形变和最大应力的影响

随着转速的增加，将近一步削弱电磁力的作用效果［7-8］。这进一步说明，当电机高速运转时，电磁力影响明显下降，最大应力作用和形变效果主要由离心力决定，因此，在高速IPM电动机的强度分析中可以只考虑离心力的作用，而将定转子间电磁力、永磁体吸引力的作用作为安全裕量。

2 简化分析模型

2.1 简化模型的建立

在进行机械应力与形变分析时，本文采用Ansys作为有限元分析软件。过程如下:将电磁有限元软件剖分后所包含节点与单元信息的数据文件导入Ansys中重新建立起电机模型，通过电磁有限元分析的结果作为边界条件，导入到结构场中进行结构有限元分析计算应力分布。由于涉及到不同应用软件平台以及物理场的切换，有限元法步骤多、计算量大。本文提出的简化模型分析方法是直接利用电磁有限元的剖分模型进行离心应力的计算和分析，流程得到大大的简化。

在电磁有限元分析软件中，将转子部分剖分成密集的三角形单元，如图4所示。当电机高速旋转时，各小三角元都受离心力作用。由于几何体较小，可以认为其离心力方向应为沿转子轴中心与三角几何体中心连线径向向外。

图4 6极Ⅰ型转子横截面mesh剖分图

则区域范围内的小三角元i所受到的离心力Fi:

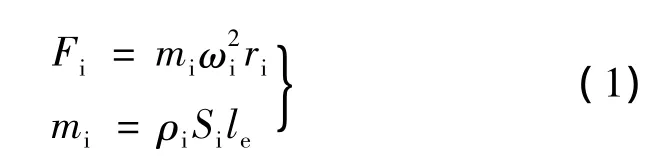
式中:ρi为小三角元所处区域的材料密度;Si为每个小三角元的面积;mi为小三角元的质量;ωi为三角元的角速度;ri为小三角元重心半径;le为小三角元的轴向有效长度(为方便分析，常取单位长度来计算)。

2.2 模型解析计算

为了方便计算，对于承受最大应力的隔磁桥区域，作相关近似计算如下。

(1)Ⅰ型IPM和未加辅助隔磁桥2的V型IPM转子

如图4、图5所示，在Ⅰ型以及未加辅助隔磁桥2的V型IPM电动机中，隔磁桥1，3将是最大离心力承受区，它主要承受的是剪切应力。产生应力的主要部分是磁钢(区域①)以及磁钢外侧的极靴铁心部分(区域②)。

假设两个隔磁桥承受所选区域单元的离心力，对离心应力Fi沿隔磁桥1和隔磁桥3的径向方向进行分解，如下:

式中:Fi1、Fi3分别为应力单元对隔磁桥1和隔磁桥3中心点施加的离心应力，θi1、θi3分别为对应单元重心与隔磁桥1、3中心之间的夹角。

对于应力来源区域内的单元进行求和，分别得到隔磁桥1、3所受的离心力F及应力τ:

式中:τ1、τ3分别为隔磁桥 1、3 所受的剪切应力，A为隔磁桥1、3剪切应力的轴向截面积，γ为隔磁桥1、3的径向宽度，le为轴向有效单位长度。

(2)存在辅助隔磁桥的V型IPM电动机

如图5所示，对存在辅助隔磁桥的V型IPM电动机中，由于辅助隔磁桥2的存在，它将大大减轻隔磁桥1、3上所承受的应力。实际上最大应力将由隔磁桥1、3转移到辅助隔磁桥2上。而此时隔磁桥2将主要承受拉伸应力，而非剪切应力。产生离心应力的部分主要有磁钢(区域①②)和极靴铁心(区域③)。

图5 V型IPM电动机转子横截面mesh剖分图

假设由上述三处隔磁桥来承受施力区域所产生的离心应力——隔磁桥1和隔磁桥3的剪切应力，以及隔磁桥2的拉伸应力，方向均为径向向外。对离心应力Fi沿隔磁桥1、2、3的径向方向进行分解如下:

由隔磁桥3与隔磁桥1的对称性可得Fi3=Fi1。

假设转子冲片的形变集中于隔磁桥1、2、3上的三个点上，同时隔磁桥1、3对称分布，故当隔磁桥2发生形变Δx2时，隔磁桥1，3应相应沿径向向上产生位移:

式中:θ12为隔磁桥1和隔磁桥2中心沿径向的夹角，它与极对数p有关

2.3 有限元法与简化模型分析的比较

本文采用简化模型分析和有限元两种方法，对不同极数下的Ⅰ型IPM转子以及有无隔磁桥下的V型IPM电动机两种情况下的离心应力进行计算与比较。验证了简化模型分析法的可行性，同时就增加辅助隔磁桥的优化设计方法进行讨论。

2.3.1 不同极数下Ⅰ型IPM转子最大应力比较

选用6极与8极的转子结构进行简化模型分析与有限元分析。两者均选用磁钢密度为7 400 kg/m3，转子冲片密度为7 750 kg/m3，切变弹性模量G=8.065×104MPa;设计参数如表1所示。

表2 两种Ⅰ型IPM电动机转子设计参数

简化模型分析法和有限元法计算的IPM电动机转子离心应力的对比如图6所示。

图6 不同极数下Ⅰ型IPM转子的简化模型分析与有限元法的计算离心应力比较

可以看到，用两种方法计算出来的离心应力结果基本一致，但用简化模型分析法所算得的应力稍小，这是因为计算时，等效的径向应力时有一部分未计入在内以及相关计算误差所致。同时也证明了简化模型分析法粗略估计转子所受最大应力的可行性。

2.3.2 V型IPM电动机隔磁桥2的作用

对V型IPM电动机有无隔磁桥2的两种不同类型进行简化模型分析计算。

两者均选用磁钢密度为7 400 kg/m3，转子冲片密度为7 750 kg/m3，拉伸弹性模量E为2.082×105MPa，切变弹性模量 G 为8.065×104MPa，设计参数如表2所示。

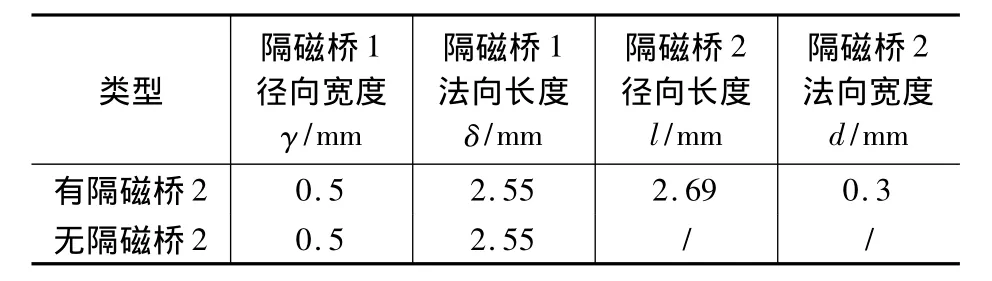
表2 V型电机IPM电动机转子设计参数

同样，将简化模型分析法和有限元法计算的V型IPM电动机转子离心应力进行对比如图7所示。图7同样可以说明了简化模型分析法的可行性。同时可以得到，在V型电机转子中，通过增加隔磁桥2，使得其转子所受的最大应力减小，这样使得在承受相同应力的条件下，存在隔磁桥2的V型电机能在更高的转速下运行。

隔磁桥宽度的变化同时会对电磁性能和结构性能都产生重要的影响。对于IPM电动机最大应力通常分布在隔磁桥区域，一方面可以通过增加其宽度来增加隔磁桥的机械强度，而另一方面，会使漏磁迅速增加而影响电机的运行性能［9-10］。

图7 V型转子(有无隔磁桥情况)离心应力简化模型分析法与有限元法比较

3 实验分析

本文采用Ⅰ型IPM电机转子结构进行实验(如图8所示)，隔磁桥原始设计为0.5 mm，为方便实验分析，将隔磁桥宽度削薄至0.2 mm。转子硅钢材料抗拉强度为250 MPa，抗剪强度取抗拉强度的0.6倍，约为162 MPa。对上述原型机进行以上两种方法进行计算分析，仿真结果表明:转速为7 000 r/min时，隔磁桥上的应力约为170 MPa，较硅钢片的抗拉强度250 MPa小，但是大于抗剪强度约为162 MPa，故很有可能出现隔磁桥断裂的情况。

图8 仿真结果及实验测试平台

IPM电动机高速旋转的实验结果如图9所示。当电机转速达到7 000 r/min时，转子冲片上的隔磁桥完全断裂，同时极靴部分也严重形变。而中间部分极靴没有明显的形变，这是由于冲片叠压的转子，两侧冲片对中间冲片的挤压起到了加固作用。相比之下，最外侧的冲片由于缺少这种挤压力，相同转速条件下更容易发生严重的形变而产生断裂。由断裂脱落的极靴形状可以看出，极靴部分的隔磁桥在断裂前已发生了严重的塑性形变。实验结果与理论分析基本一致，这进一步验证了本文所提出简化模型分析法的可行性。

图9 电机旋转至7 000 r/min后，转子的受损情况

4 结 论

本文对两种常用转子结构的IPM电动机的形变和应力进行了分析。同时提出了一种灵活高效的简化模型分析法来计算转子离心应力。

(1)考虑到在永磁电机高速运行时，其机械应力大部分由离心应力引起，故采用简化分析模型可以估算出其所能承受最大应力。电磁和结构有限元计算可以分析电磁力和离心力的影响，但是计算复杂、步骤较多。

(2)隔磁桥是内嵌式转子结构最容易断裂的部分，增加隔磁桥的宽度能够增强其机械强度，但是会降低电机的电磁性能。在V型IPM电动机中，隔磁桥2能够有效地增强极靴部分的强度，但是也增加了额外的漏磁路径。所以，平衡电磁和结构两方面的性能是优化设计隔磁桥时应重点考虑的问题。另外增加极靴孔并选择合适孔半径对降低离心力，降低转子的最大形变亦有一定的帮助。比较两种转子结构，V型IPM结构具有能够承受更大的机械应力，结构更坚固。

［1］ 王继强，王凤翔，鲍文博，等.高速永磁电机转子设计与强度分析［J］.中国电机工程学报，2005，25(15):140-145.

［2］ 韩则胤.内嵌式转子无刷直流电机驱动系统在汽车电动空调中的应用研究［D］.杭州:浙江大学电气工程学院，2009:61-94.

［3］ Kim Y K，Lee J.A comparative study of high-speed permanent magnet synchronous motor for air compressor［C］//in INTMAG，2005:663-664.

［4］ Ha K H，Hong J P，Kim G T，et al.Mechanical Vibration and Stress Analysis of the Link of Interior Permanent Magnet type Synchronous Motor［C］//Interuational Conference on Electric Machines and Drives，1999:150-152.

［5］ Lovelace E C，Jahns T M，Keim T A，et al.Mechanical design considerations for conventionally laminated，High-Speed，Interior PM Synchronous Machine Rotors［J］.IEEE Trans.on Industry Appli.，2004，40(3):806-812.

［6］ Lee K J，Kim K C，Lee J.Bridge optimization of interior permanent magnet motor for hybrid electric vehicle［C］//Magnetics Conference.INTERMAG，2003:GQ-07.

［7］ Lee K J，Kim K C，Lee J.Rotor optimization of interior permanent magnet synchronous motor considering mechanical stress［C］//Magnetics Conference.INTERMAG Asia，2005:717-718.

［8］ Jun C H.Analysis of the mechanical stresses on a squirrel cage induction motor by the finite element method［J］.IEEE Transactions on Magnetics，1999，35(1):1282-1285.