任务与有效可用度在备件计算中的对比分析
王剑平,魏曙寰,陈国卫
(1.海军驻武汉701所军事代表室,湖北 武汉 430064;2.海军工程大学船舶与动力学院,湖北 武汉 430033)
备件配置优化,是指为保证达到系统的使用需求,对相关备件(如备件数量和种类的确定、备件储存位置选择等)的一系列问题的求解,其核心是对备件存储的品种和数量的确定[1~2]。
一般情况下,装备的战备完好性和任务成功性与备件的品种和数量密切相关,所以备件优化问题常与装备的使用可用度、任务成功率等相关联[3~5]。
NATO针对舰船装备,考虑舰船自身的维修和保障能力,给出了任务期内使用可用度的海军经验公式,称之为有效可用度(Effective Availability)[6]。有效可用度仅为NTAO的海军经验公式,未见其确定机理或实际数据决策应用的相关文献,尚不能为其他海军或民用设备提供决策参考。
本文将任务可用度与有效可用度经验公式对比分析,显示了任务可用度的优势;在此基础之上,分别解析了寿命服从指数分布的备件在故障发生后,采用更换策略时,备件携行量与任务可用度、有效可用度的关系;最后应用Monte-Carlo方法,验证了本文所得任务可用度与备件携行量关系式的正确性,且所得结果优于依据NATO给出的有效可用度经验公式所得结果。
1 任务可用度与有效可用度的对比分析
任务可用度,指的是装备在任务期间的使用可用度。定义ART为装备的有效修理时间(修复性修理时间);Missiontime为任务时间;PMdowntime为任务期间预防性检修总停机时间;TBCF为装备可修严重故障间隔时间;TTCFmf为装备执行任务时发生不可修严重故障导致任务失败的时间。基于任务成功率的任务可用度计算式为[2]
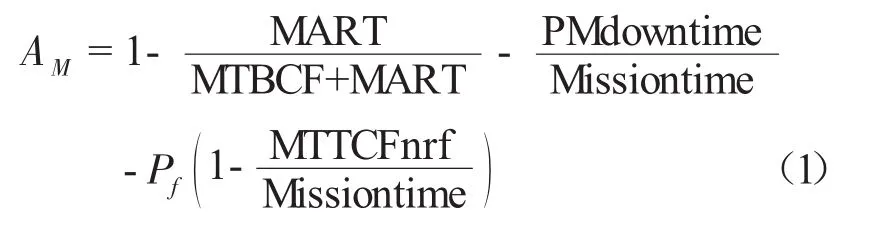
NATO给出的舰船装备的有效可用度(Effective Availability)的经验公式为[6]

其中,
MTBCF为海上可修平均严重故障间隔时间;
MART为平均有效修理时间;
PMdowntime为任务期间预防性检修总停机时间;
MTTCFnr为海上不可修平均严重故障间隔时间;
Missiontime为任务时间。
这里将影响任务完成的故障称为严重故障。
对比分析式(1)和式(2)后,可以得到以下结论:
任务可用度AM与有效可用度AE均是装备在任务期间使用可用度的简单、易用的解析形式。
式(1)和式(2)中的

实际上为装备的固有可用度,在装备列装前已由设计方确定和提供;
依据任务时间和装备的使用保养规程,确定预防性维修项目和次数后,PMdowntime也可以很容易计算得到。
1-MART/(MTBCF+MART–Pmdowntime/Missiontime
实际上是装备在任务期间的可达可用度,即任务必定成功情况下的使用可用度。
因此,确定装备任务期间的可用度,仅需进一步分析任务成功与否对使用可用度的影响。
AM将任务成功与否,对任务期间使用可用度的影响解析为
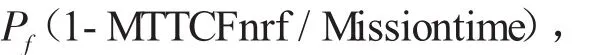
即装备发生严重故障导致任务失败后,剩余任务时间均值与任务时间的比值与任务失败率的乘积;
根据NATO海军大量的实测数据,AE将任务成功与否对任务期间使用可用度依据经验表示为
0.5 Missiontime/MTTCFnr,
需要指出的是
0.5 Missiontime/MTTCFnr
是综合舰艇任务期间备件储备、人力资源、海上维修条件(某些故障本身是海上不可修的)等多种保障资源影响因素的经验公式。
由于AE是综合舰艇任务期间备件储备、人力资源、海上维修条件(某些故障本身是海上不可修的)等多种保障资源影响因素的经验公式,因此若应用AE分析某单项保障要素,如备件携行量对任务期间装备使用可用度的影响,可能会造成较大的误差,造成决策失误。
而AM为装备在任务期间使用可用度的解析式,通过进一步明确AM与各种保障要素之间的关系,可以确定各种保障要素的任务要求,AM在装备保障资源决策方面优于AE。
2 任务期的使用可用度与寿命服从指数分布的备件携行量的关系式
假设装备在任务期间发生严重故障后,采用更换维修策略,则备件短缺将会导致任务失败。备件任务期间的寿命,服从参数为λ的指数分布[2]。
由于备件的寿命服从参数为λ的指数分布,不必进行预防性维修。AM为
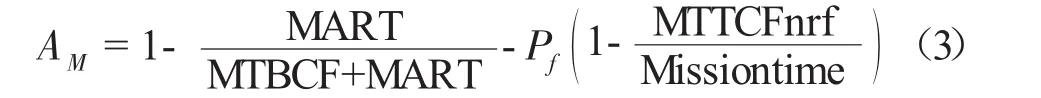
采用更换维修策略时,装备的有效修理时间即为备件更换时间,且有效修理时间并非本文分析的重点,因此可认为是定值。MTBCF为备件的寿命期望1/λ,Missiontime为输入变量,则Pf与是需要确定的变量。
由文献[2]可知,任务期携带n个备件时的任务失败率Pf即为发生n+1及以上次故障的概率
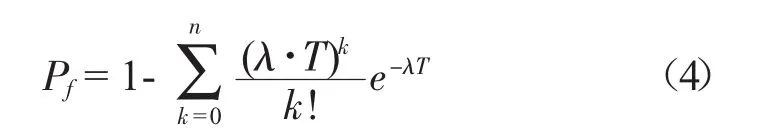
其中T为任务时间,即Missiontime。
AM与备件携行量的关系式为

由于备件的寿命服从参数为λ的指数分布,不必进行预防性维修。式(2)化简为

采用更换维修策略时,装备的有效修理时间即为备件更换时间,因此可认为MART是定值。MTBCF为备件的寿命期望,Missiontime为输入变量,MTTCFnr是需要确定的变量。
AE与寿命服从指数分布的备件携行量的关系式为
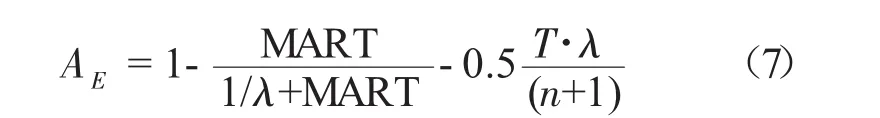
3 数值算例与仿真验证
采用文献[2]中的数据,假设舰艇某部件寿命服从分布参数为λ=1/720 h-1的指数分布。采用更换维修策略,每次更换维修时间为8 h,任务时间为2 160 h(90 d)。依据式(5)和式(7),可以计算得到备件携行量n与AM、AE的关系,如表1所示。

表1 AM和AE与备件携行量的关系
由表1可知,由于AE是综合舰艇任务期间备件储备、人力资源、海上维修条件(某些故障本身是海上不可修的)等多种保障资源影响因素的经验公式,应用AE分析备件携行量的影响,出现了不合理的结果:当备件携行量n为0时AE为-0.511 0,而实际上可用度不可能为负值,显然是不合理的。因此,可以通过仿真方法进一步验证AM的正确性。
在执行任务期间,装备的维修保障流程为:任务开始后,装备投入使用;当装备发生严重故障时,如果有备件更换,而且任务时间满足备件更换时间,则对装备进行备件更换;备件更换后,装备重新投入使用;装备正常工作直到任务完成,则任务成功;当装备发生严重故障时,如果没有备件更换,或任务时间无法满足备件更换时间,则任务失败。对于舰艇某部件寿命服从指数分布,分布参数为λ=1/720 h-1,采用更换维修策略,每次更换维修时间MART为8 h,任务时间T为2 160 h(90 d)的任务过程仿真1万次后,得到装备的任务期间使用可用度Ao与备件携行量的关系,并与表1中AM所得结果对比,见表2。
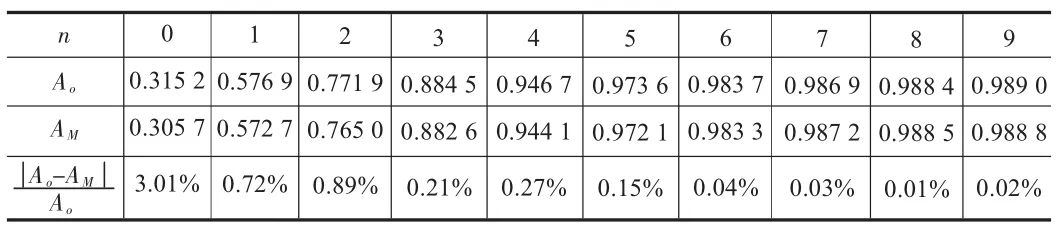
表2 Ao和AM与备件协行量n的关系
由表2可知,Ao与AM之间的误差较小,其中:最小相对误差为0.01%,最大相对误差为3.01%。因而可认为备件携行量与AM之间的关系,与实际任务过程是相同的。因为任务过程不进行预防性维修,装备的任务可达可用度为
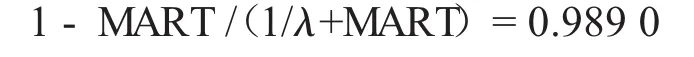
当备件携行量为6个时,装备任务期间的使用可用度与可达可用度基本一致,装备在任务期间的可用性已发挥至99%(0.9837/0.9890或0.9833/0.9890)以上。
4 结束语
任务可用度AM与NATO针对舰船装备的有效可用度AE经验公式对比分析显示:AE是综合舰艇任务期间备件储备、人力资源、海上维修条件(某些故障本身是海上不可修的)等多种保障资源影响因素的经验公式,因此若应用AE分析某单项保障要素,如备件携行量对任务期间装备使用可用度的影响,可能会造成较大的误差,造成决策失误。而AM为装备在任务期间使用可用度的解析式,通过进一步明确AM与各种保障要素之间的关系,可以确定各种保障要素的任务要求,AM在装备保障资源决策方面优于AE。
基于任务可用度AM的备件携行量与基于仿真方法的备件携行量对比分析显示:两种方法确定的备件携行量基本一致,通过任务可用度AM确定的备件携行量真实地反映了任务对备件的需求,可以作为装备保障决策的依据。
[1]Kennedy W J,Patterson J Wayne,Fredendall Lawrence D.An overview of recent literature on spare parts inventories[J].Int.J.Production Economics,2002,(76):201-215.
[2]张汝政,魏曙寰,陈砚桥.基于任务可用度模型的指数分布型备件随舰携行量计算模型[J].海军工程大学学报,2011,23(4):70-73.
[3]王佩高,金家善.随舰备件动态管理及备件数量计算模型[J].海军工程大学学报,2005,17(3):103-106.
[4]张建军,刘 芳,张 涛,等.基于BCMP排队网络的作战单元备件保障度评估模型[J].兵工学报,2009,30(1):110-113.
[5]郭继周,赵朝先,郭 波.面向多阶段任务的武器系统备件优化配置[J].数学的实践与认识,2009,39(12):64-70.
[6]NATO.ARMP-4:Guidance for Writing NATO R&M RequirementsDocuments(4th Ed.)[S].2008.

