用杠杆法计算行星齿轮机构的啮合效率
李明圣
(湛江师范学院物理科学与技术学院,广东 湛江 524048)
传动比法,对求封闭式差动行星传动的啮合效率很方便,即只要求得传动比公式,便可以写出效率计算公式。但公式中的指数x(等于+1或–l)通常需求偏导数才能确定,运算繁琐。
卢存光、段钦华在文献[1]对传动比法指数x的含义做了分析,给出了确定指数x的判断依据,使传动比法的应用更简单。指数x由转化机构中啮合功率流向确定,啮合功率计算虽然不用求偏导数,功率流向计算过程还是比较繁琐。
本文提出一种新的确定啮合功率流向方法——杠杆法。用此法不但可以快速求出多排并联行星轮传动比,通过转速图和受力图,可以方便判断各行星轮的啮合功率流向,容易确定指数x的取值,是计算行星轮系传动的啮合效率很有效方法。
1 杠杆法
杠杆模拟法是将行星轮系中3个基本构件(太阳轮、齿圈和行星架)的角速度,模拟为一垂直杠杆上3个不同点对应的水平线速度,将轮系中3个基本构件受到的扭矩,模拟为杠杆上对应点受到的力。杠杆模拟法的优点,是将一个旋转运动系统模拟为人们熟悉的直线运动系统,从而可以直观地对轮系各构件的受力情况进行分析。
如图1(a)所示,是单级单行星齿轮系的结构简图,图1(b)是单级单行星齿轮系的一垂直放置的模拟杠杆图。杠杆图的3个构件点(a、b、H)分别代表单级行星齿轮系太阳论、齿圈和行星架。

图1 单级单行星齿轮系示意图
具有2个自由度3个构件点的角速度,满足以下关系式:
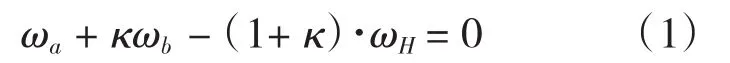
式中,
κ为行星轮系的特性系数,κ=Zb/Za;
ωa、ωb、ωH分别代表单级行星齿轮系太阳轮、齿圈和行星架的角速度,下同。
根据能量守恒定理,不考虑齿轮副摩擦,设Ma、Mb、MH分别表示太阳轮、齿圈和行星架所受到的转矩,3个构件点所受力矩之间,满足以下关系式:

考虑齿轮副摩擦,3个构件点所受力矩之间满足以下关系式[2]:
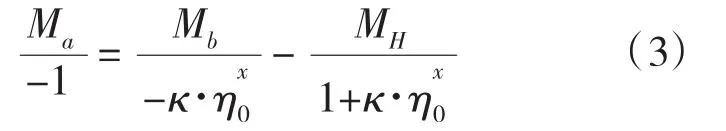
式中,
η0为转化机构的效率,按定轴轮系效率公式确定;
若用η1、η2分别表示太阳轮与行星轮、齿圈与行星轮啮合时的传动效率,则有

这3个构件点所受力矩方向,可以从图1(c)受力图获得,行星轮系的传动比,可以由式(1)角速度关系式计算,也可以从图1(b)杠杆图中相似三角形关系获得。
2 5HP-24自动变速器结构分析
图2所示是ZF公司生产的5速电子控制的5HP-24型自动变速器传动示意图,该型号自动变速器用于 2003款以后的路虎(Land Rover)、宝马(BMW540、740、X54)、捷豹(Jaguar XK8、XJ8)等。

图2 5HP-24自动变速器传动简图
由图2可知,5HP-24自动变速器行星齿轮组,由3个单级行星齿轮机构组成。行星排1的行星架,与行星排2的内齿圈相连;行星排1的内齿圈,与行星排2的行星架及行星排3的内齿圈相连;行星排2和行星排3的太阳轮相连。行星排3的行星架,是动力输出端。
变速器内部共有7个换档执行元件,包括3个离合器、3个制动器和1个单向离合器。各换档执行元件的作用,如表1所列。
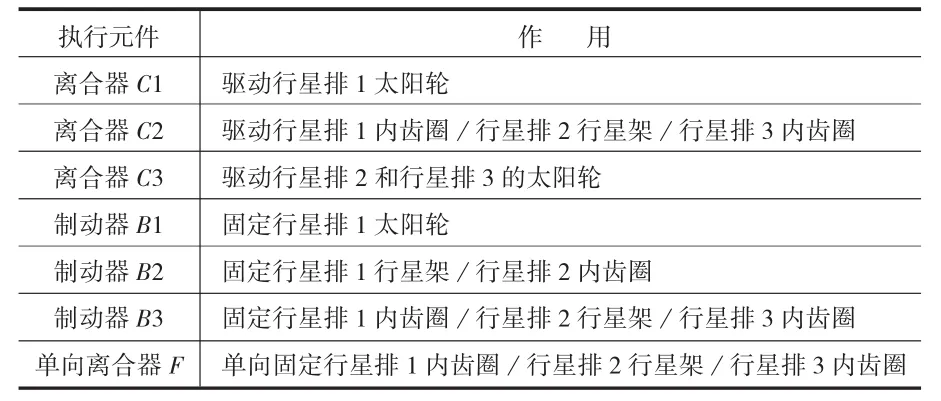
表1 5HP-24自动变速器换档执行元件的作用
各档传动比的大小,如表2所列。

表2 5HP-24自动变速器各档传动比值[3]
3 5HP-24行星轮系啮合效率计算
3.1 建立5HP-24传动机构的杠杆图
三行星排并联时,每个行星排视为1个垂直的杠杆和3个支点,行星排之间的构件相互连接,在杠杆图上视为各支点之间的连接。
三行星排并联时,在杠杆图上有5个支点,在处理时,根据需要,既可以将杠杆重叠,又可以将杠杆分开。重叠时,将相互连接的部分合并为一个点,将杠杆分开时,连接点用一水平线来表示。两种情况都要对杠杆的力臂进行调整,调整时要保证连接部分合并点之间的力臂长度相等,并且各杠杆力臂长度比不变,这样将多个行星排的杠杆图合并为一个总杠杆图,并在图上标上离合器C、制动器B、单向离合器F以及输入构件i、输出构件o,即得多行星排并联机构的转速杠杆图[4]。
如图3所示为5HP-24杠杆图,图(a)为杠杆总图;图(b)为转速图,C3B3(或 F)接合得到 1 档,连C3B3与H3相交,交线段长度为输出转速的大小,方向与输入同向。同样方法C3B2接合得到2档,C3B1接合得到3档,C3C2接合得到4档,C2B1接合得到5档,C1B3接合得到R档。各支点的距离由行星轮的特性系数κi决定。

图3 5HP-24杠杆图
3.2 计算5HP-24传动机构各档位下传动比
由图4(c)转速图,假设输入件构件的转速为1,制动件构件转速为0,输出构件转速为该档位的转速线的长度,方向与x轴向同为正,相反为负,利用相似三角形的关系,求各档的传动比。
设 AC=a、CE=b、ED=1、DB=c,其中,

各档的传动比见表2。
从转速图可见,三行星排这种并联布置形式,可实现6个前进档,但这款变速器只采用前五档。
知道变速器各档的传动比,根据传动比法[1],可
3.3 运动分析与效率计算
以写出各档齿轮啮合效率计算公式,限于篇幅,本文选择传动路线最为复杂的前进3档为例,则前进3档啮合效率式:
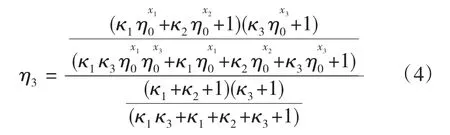

表3 5HP-24自动变速器各档传动比
根据表2和表3,可计算出

如图2所示,可知三排行星齿轮组,均为单排单行星齿轮结构。若所用齿轮均选用圆柱斜齿轮,精度均为8级,采用油润滑,则每级齿轮的传动效率η可取为 0.98,则

前进3档的动力传动路线,离合器C3接合,制动器B1接合:
行星排3:太阳轮a3、齿圈b3为输入,两者转速不同,行星架H3减速同向输出;
行星排2:太阳轮a2、齿圈b2为输入,两者转速不同,行星架H2减速同向输出;
行星排1:行星架H1输入,太阳论a1固定,齿圈b1增速同向输出。
根据以上动力传递路线的分析,做出3个行星排的转速图和受力图(如图 4 所示),(a)、(b)、(c)为行星排1、2、3的转速图和受力图,并用图4来判断指数x的值。
(1)行星排 1:ωa1-ωH1<0,则得 x1=-1;
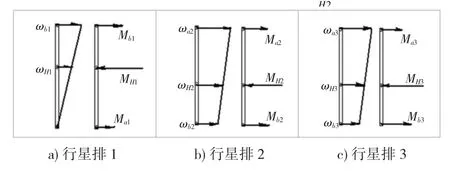
图4 前进3档的转速图和受力图
(3)行星排 3:ωa3-ωH3>0,则得 x3=+1。
将 κ1=2.59,κ2=3.13,κ3=2.57,x1=-1,x2=+1,x3=+1,η0=0.982代入式(4),求出前进 3 档啮合效率:

4 结束语
运用杠杆法计算行星轮系的啮合效率,首先根据行星轮机构的结构特点,画出行星轮机构的杠杆总图,确定机构动力传递路线,求出传动比;根据动力传递路线和构件间受力平衡关系,画出单个行星轮系的转速图和受力图,并由此图判断各单个行星轮系的功率流向,确定传动比法指数x的取值。
[1]卢存光,段钦华.传动比法(KpeЙHec法)的研究[J].机械传动,2003,27(2):19-20.
[2]公彦军,赵 韩,黄 康,等.拉维娜行星齿轮机构的运动分析和传动效率计算[J].设计与研究,2010,(9):9-11.
[3]谢代鹏,黄宗益,王 康.BMW轿车五档自动变速器[J].上海汽车,1999,(2):7-10.
[4]李兴华,何国旗.等效杠杆法分析行星齿轮传动[J].机械传动,2004,(1):44-45.

