构造A-伸缩MRA小波集的一种新方法
李万社, 史会婷
(陕西师范大学数学与信息科学学院, 陕西 西安 710062)
0 引 言
小波分析是近几十年发展起来的一个新的数学分支,广泛应用于通信、图像处理、信号处理等领域,并且取得了巨大的成就.但是我们又知道构造一类实用的小波是非常困难的,尤其是构造同时具有正交性、对称性、紧支撑性等的小波.为了解决这一难题,20世纪90年代后期,Dai和Larson在文献[1]中提出了小波集的概念:用来描述一个可测集合E⊆R,使得χE(χE为E的特征函数)的IFT变换是二进正交小波(这里的正交小波是指一个函数ψ∈L2(R)经过连续的伸缩平移变换后成为L2(R)的正规正交基).后来,文献[2]把这样的小波集推广到了高维空间中,并研究了它的一些性质,许多文献已经证明非二进伸缩因子的小波集是存在的,其中文献[3,4]证明在n维空间中,伸缩因子为A(A为n×n的可扩张矩阵)的小波集也是存在的.
经过长时间的发展,小波集的理论有了较大的发展,尤其在一维空间中,利用小波集的思想构造小波已经取得了很大的成果,如Eugen和X.Dai等人分别在文献[1,4]中研究了伸缩因子为实数时的小波集的构造方法.在高维空间中,学者在小波集的构造方面也有一定的研究,但都有一定的局限性,如X.Dai等人在文献[3,5]中探讨了高维空间中框架小波集的构造方法,Marcin在文献[6]中研究了Riesz小波的构造方法,但是他们都没有直接构造高维空间中的小波集.后来,Marcin和Qing Gu分别在文献[7,8]中构造了高维空间中的小波集,但是文献[7]中的构造方法仅限于|det(A)|=2时的情形,对于其它的可扩张矩阵A却不一定适用.而文献[8]报道了对多小波的构造.
基于上述原因,本文在前人研究的基础上,在高维空间中,对于任意的可扩张矩阵A,利用映射的思想,探讨了A-伸缩MRA小波集的构造方法,再利用小波集的定义得到了小波.
1 基础知识
定义1:L2(Rn)空间中的MRA即为L2(Rn)空间中一列嵌套的闭子空间{Vj∶j∈Z}满足下列的性质:




引理1[9]若T是Q=[-π,π]n到Rn的任一映射,且满足对任意的x∈Q有At(T(x))≡x,则存在一个集合E⊆Rn和一个映射T′∶E→E,使得(T,T′)是集合E的A-补对.
注: 该定理说明了对满足条件(At(T′(x))≡x)的映射T,都存在一个可测子集E及一个映射T′,使得(T,T′)满足集合E的A-补对定义,即证明了可测子集E及T的存在性.

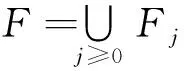
引理3[7]可测集合E=Rn是小波集的充要条件为

(1)

2 A-伸缩MRA小波集的构造
定理1若A为n×n的可扩张矩阵,E为Rn的可测子集,E与2π是平移同余的,且余集为空集,E包含原点的邻域且该邻域的测度为零,设(T,T′)是集合E的A-补对,则W=A′EE是一个MRA小波集.

(2)
对任意的x∈Rn,设y=(At)-1(x+2πj)∈ET(Q),则存在z∈T(Q)及m>0,使得y=T′m(z).
因此x≡AT(y)≡T′m-1(z),这表明存在k∈Zn,使得x+2πk∈E.
若(2)的左边为零,则右边也必须为零.否则,设x1,x2,…是E中形如x+2πk的一列完备点列,则T′(x1),T′(x2),…是ET(Q)中的不同元,且T′(x1),T′(x2),…的形式都为(At)-1(x+2πj).
若z是ET(Q)中形式为(At)-1(x+2πj)的任意一个元,则存在w≡x使得z=T′(w),则z必然是T′(x1),T′(x2),…中的某一个,因(2)式中左边的非零元与右边的非零元是一一对应的,故χE满足容许性方程(1).
由于E在(At)-1下不变,故有E⊆(At)-1E,令W=At(E)E,易知
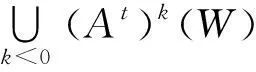



定理2设A是n×n的实可扩张矩阵,则存在一个A-伸缩MRA小波集.
证明:易知很容易选择一个可测集合Q⊆Rn(使其包含原点的邻域且该邻域的测度为零)和一个映射T∶Q→Rn是一一映射且满足∀x∈Q有At(T(x))≡x.



由定理1知,W=AtEE是A-伸缩MRA小波集.
总结: 定理1及定理2表明,任意满足条件的可测集合都可以通过A-补对构造小波集,进而构造A-伸缩MRA小波.
在文献[7]中也给出了n维空间中一类小波MRA的构造方法,为了读者的方便,我们将给出这些结论.
定理3若A是n×n的实可扩张矩阵且|det(A)|=2,并且AZn⊂Zn,当F是n维空间中一个包含零的邻域的可测子集,如果F⊂AtF且F与Ω是2π平移同余的,且余集为空集,则E∶=AtFF是一个A-伸缩MRA小波集.
定理4若A是n×n的实可扩张矩阵且|det(A)=2|,则存在一个A-伸缩MRA小波集.
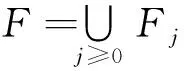
文献[8]中也给出了n维空间中,对任意的可扩张矩阵,一类r-正则MRA小波的构造方法,内容如下:

定理6设A是n维空间中的任意一个可扩张矩阵,且|det(A)|=b(b为实数),则对任意的可扩张矩阵A都存在一个r-正则MRA及包含(b-1)个函数的r-正则小波类.
不难发现,定理5及定理6给出了n维空间中MRA多小波的一种构造方法,而且这类r-正则的正交多小波具有消失时刻,这个事实在文献[8]中已经得到证明,这3种构造MRA小波的方法都具有各自的优缺点.本文之所以选择利用映射的思想构造MRA小波是因为映射比较熟悉且容易构造,尤其在某些时候我们可以直接利用所熟悉的映射构造实际需要的小波.
3 构造算例
本文定理1及定理2给出了构造A-伸缩MRA小波集的方法,具体步骤如下:
(1) 选择可测子集E,使其满足E与Ω是2π平移同余的,且余集为空集,E包含原点的邻域且该邻域的测度为零.
(2) 令Q=[-π,π]n,取映射T∶Q→Rn, 使其满足对任意的x∈Q,At(T(x))≡x,则由引理1知,存在一个E到E的映射T′(T′最简单的选择就是令T′=(At)-1)使得(T,T′)是集合E的A-补对.
(3) 令W=AtEE,由定理1知,可测子集W是一个MRA小波集.
下面我们利用定理1及定理2的方法,根据以上的具体步骤构造一些简单的A-伸缩MRA小波集,最后再利用定理3的方法构造一些简单的MRA小波集.
例1 在一维空间中用本文定理1及定理2的方法构造A-伸缩MRA小波集.




在下面例子的构造过程中,为了书写的方便,用顶点坐标表示二维空间中所形成的区域,如conv{(1,-1),(0,1),(1,0)}表示顶点坐标分别为(1,-1),(0,1),(1,0)所形成的三角形区域.


再令A=conv{(-1,2),(-1,1),(0,1)},B=conv{(1,-2),(1,-1),(0,-1)},C=conv{(-1,1),(0,1),(1,0),(1,-1),(0,-1),(-1,0)}.
记作:
则2π(A′∪B′∪C)是空集,因此F2是2π平移同于Ω且余集为空集,简单计算后发现AtF=conv{(0,2),(-2,2),(0,-2),(2,-2)}, 因此AtF⊃F,AtFF是空集.
4 结束语
本文在前人研究的基础上,进一步探讨了高维空间中伸缩因子为可扩张矩阵A时,A-伸缩MRA小波集的构造方法.该方法引进A-补对的定义,首先构造两个满足一定条件的映射T及T′,然后再利用映射的思想构造满足条件的可测子集E,并令W=AtEE,最后证明了W即为A-伸缩MRA小波集,但是这种构造方法在子空间中是否依然成立还没有得到论证.本文同时还引进了两种构造A-伸缩MRA小波集的方法,并且对这3种方法加以比较.最后,本文利用这3种方法构造了一些简单的A-伸缩MRA小波集.
参考文献
[1] Eugen J.Lonascu,David R.Lrason, Carl M.Pearcy.On wavelet sets[J].The Journal of Fourier Analysis and Applications, 1998,6(4):711-721.
[2] Xingde Dai, Darid R.arson, Darriin M.Speegle.Wavelet sets inRn[J]. Fourier Anal.,1997,(5):451-456.
[3] X.dai, Y.diao, Q.GU, D.Han. Wavelets with frame multriesolution analysis[J]. The Journal of Fourier Analysis and Applications, 2003,1(9):39-48.
[4] X.Dai, D.Larson. Wandering vectors for unitary system and orthogonal wavelets[J]. Memoris of the AMS,1998,134(640):1-50.
[5] X.dai, Y.diao, Q.GU, D.Han.Frame wavelet sets inRd[J].Journal of Computational and Applied Mathematics, 2003, 155:69-82.
[6] Marcin Bownik.Riesz wavelets and generalizedMRA[J].Applied and Computational Harmonic Analysis, 2003, 14:181-194.
[7] Qing Gu, Deguang Han, D.Han.Wavelets with frame multriesolution analysis[J].The Journalof Fourier Analysis and Applications, 2000,4(6):437-447.
[8] Marcin Bownik. The construction of r-regular wavelets for arbitrary dilations[J]. The Journal of Fourier analysis and Applications, 2001, 5(7):489-506.
[9] Lawrence W.Baggett, Herbert A.Medina, Kathy D.Merrill.Generalized multriesolution analysis, and construction procedure for all wavelet sets inRn[J]. The Journal of Fourier analysis and Applications, 1999, 6(5):563-573.

