利用微元法简化对面积的曲面积分计算
2012-02-15 06:38:18林玎
吉林建筑大学学报 2012年6期
林玎
(吉林建筑工程学院基础科学部,长春130118)
0 引言
1 设Σ是球面或球面的一部分,球面方程:x2+y2+z2=R2
利用球面坐标[2],该球面的方程为r=R.又设Σ:r=R.α≤θ≤β,γ≤φ≤ω.
利用球面坐标的坐标面φ=常数,θ=常数;把积分曲面Σ分成许多小块曲面,则曲面的面积微元为:

曲面上任一点(x,y,z)与球面坐标(r,φ,θ)之间的关系为:

所以,
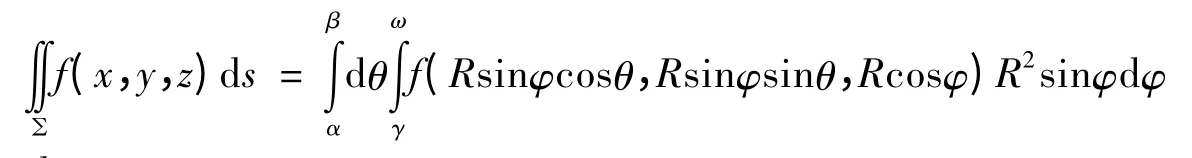
解 用球面坐标计算,由(1),(2)式得:
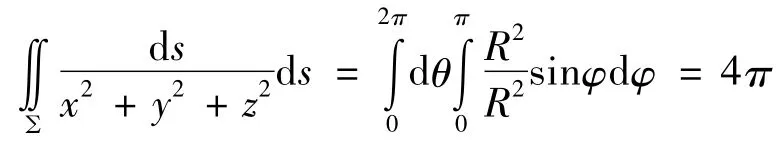
2 设Σ是柱面或柱面的一部分,柱面方程:x2+y2=R2
利用柱面坐标(r,θ,z),该柱面的方程为r=R,又设Σ:r=R
α≤θ≤β,φ1(θ)≤z≤φ2(θ),以坐标面z=常数,θ=常数,
分割曲面Σ,设ds为上任一小块曲面,则曲面微元ds=Rdθdz,曲面上任一点(x,y,z)与其柱面坐标(r,θ,z)之间的关系为:
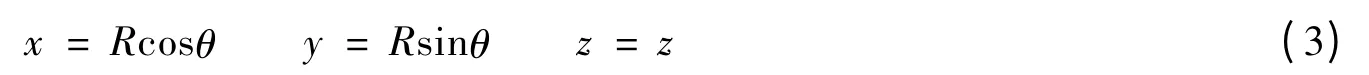
所以,
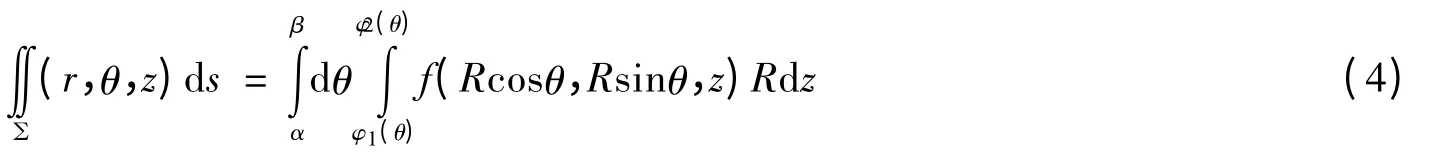
解:利用柱面坐标,由(3),(4)式得:
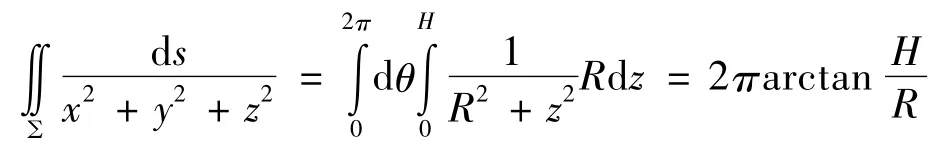
下面介绍一个灵活利用球面坐标计算曲面积分的例子
例3求圆柱面x2+y2=2xa(a>0)被锥面和坐标面xoy所截的面积
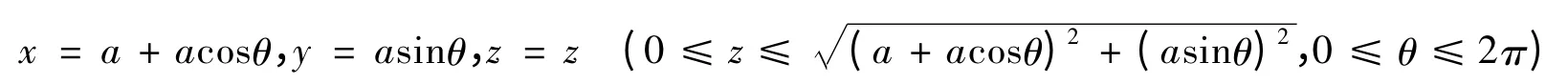
在Σ上用θ=常数的直线(平行于z轴)和z=常数的平面分割曲面Σ,面积元素ds=adθdz

3 结语
由例1~例3可见,利用微元法把曲面微元转化成两个变量微分之积,对面积曲面积分的计算方便快捷,效果较好,可在以后教学中借鉴.
[1]张永明.计算柱面上对面积的曲面积分的一种新方法[J].数学的实践与认识,2008(4):201-203.
[2]同济大学数学系.高等数学(下册)[M].北京:高等教育出版社,2007:215-218.
猜你喜欢
河北理科教学研究(2020年3期)2021-01-04 01:49:32
制造技术与机床(2019年8期)2019-09-03 01:14:40
重型机械(2019年3期)2019-08-27 00:58:46
现代计算机(2019年11期)2019-05-27 01:18:58
邵阳学院学报(自然科学版)(2019年3期)2019-05-04 04:12:48
电脑与电信(2018年11期)2018-02-16 05:41:16
数学物理学报(2017年2期)2017-06-05 09:12:31
发明与创新·中学生(2016年3期)2016-03-29 04:44:22
中学生数理化(高中版.高二数学)(2016年4期)2016-03-01 03:46:22
西安建筑科技大学学报(自然科学版)(2014年5期)2014-11-10 02:34:30

