CR系统中基于博弈论的频谱分配算法及仿真

孙爱伟 ， 张 杭 ， 路 威 ，王 萌

（1.解放军理工大学通信工程学院 研究生3队，江苏 南京 210007；2.解放军理工大学通信工程学院 卫星通信系，江苏 南京 210007；3.解放军理工大学通信工程学院 训练部，江苏 南京 210007）

电磁频谱反映了电磁辐射在各个频段和波段上的分布状况，作为一种传递信息的重要资源，在现代战争中往往成为战争双方必争的焦点之一，而且，随着军队信息化建设的高速发展，它已经成为影响战争进程甚至决定战争胜负的重要砝码。未来战场具有装备数量多、种类齐全、电台密度大、程式复杂、电磁环境变化快等特点，如果不加强电磁频谱管理，势必会造成设备相互之间的干扰。电磁频谱作为有限的国家资源和重要的战略资源，除部分分配给军队专用外，大部分是军民共用的，各国十分重视其利用效率，而据调查世界各国授权频段的平均频谱利用率不足5%[1]。

伯克利分校的一项实验结果表明，在全球授权频段，即使是信号传播特性较好、需求非常紧张的300 MHz～3 GHz频段内，频谱利用率也不到6%；在3～4 GHz频段，频谱利用率降低为0.5%；在4 GHz以上，频率利用率则更低。因此，如何对频谱资源进行有效管理和利用，充分提高频谱利用率成为亟待解决的问题。频谱利用率低下的现状对频谱的军民统筹管控技术提出了更高的要求，目前静态的频谱管理方式已无法满足要求，在很大程度上限制了频谱的高效利用，为解决这一问题，人们提出先进的调制技术、编码技术以及多天线技术、链路自适应等新技术。这些技术从不同的角度提高了信道容量，取得了较好的效果。然而，由于受到香农极限的限制，人们不可能无限制地提高信道容量。针对以上状况，认知无线电技术（CR，Cognitive Radio）应运而生，1999年瑞典皇家学院的Mitola博士提出了认知无线电（CR，Cognitive Radio）的概念旨在实现频谱的灵活、高效管理，进而提高电磁频谱的利用率[1－2]，CR 技术通过 动态频谱 共 享 （DSS，Dynamic Spectrum Sharing）来提高无线电频谱的利用效率。CR系统是一种智能无线通信系统[1－2]，它能感知周围环境，运用“理解一构建”的方法来从周围环境中获取信息，并通过实时改变诸如传输功率、载频、调制方式等传输参数来适应运行环境的变化，从而达到提高频谱利用率、缓解频谱资源紧张的目的[3]。

1 认知无线电和博弈论

认知无线电技术能够为无线电设备提供各种性能，如频谱灵活性、自适应调制、功率控制等[4－5]，其关键技术为动态频谱管理，而作为频谱管理重要组成部分之一的频谱分配，在通信领域也得到了广泛的研究，目前对于频谱分配的研究主要采用模型化的方法，而常用的模型主要有基于图论着色理论模型的方法[7-8]、基于干扰温度模型的方法和基于定价拍卖理论模型的方法[9]。

以上模型为认知无线电中的频谱分配提出了解决问题的框架。然而，基于图论模型的频谱分配完成时间与空闲信道数的多少以及网络的动态特性有关，不适应认知无线电中空闲频谱快速时变的要求，也不适应网络动态变化环境下的频谱分配研究；基于定价拍卖的模型适合于主次用户间为租用关系的认知无线电系统，应用范围具有局限性；基于干扰温度的频谱分配模型对于调制方式及干扰门限等要求固定，无法实现动态灵活的频谱切换及频谱选择。一方面，为推动认知无线电频谱分配技术的发展，提出新的频谱分配模型已成为迫切需要；另一方面，在频谱分配算法设计过程中，涉及了大量的策略选择问题。因此，基于博弈论的频谱分配模型成为当前认知无线电技术中的研究热点之一。博弈论最大的特点是能够为相应的博弈过程找到纳什均衡点，而纳什均衡点有时也正是策略最优点。这样，博弈论就可指导和分析我们的算法设计，使我们对某些问题的研究找到最优策略。

认知无线电中有关策略选择的关键问题研究的核心都是相关算法的设计和分析。可以利用博弈论对这些自适应算法进行分析，在分析的过程中，主要需要确定以下4个方面的基本问题：

1）算法是否具有稳定状态；

2）这些稳定状态是什么：

3）这些稳定状态是否是所需要的；

4）算法收敛到稳定状态所需要的约束条件。

2 博弈论模型及算法设计

2.1 博弈论模型

利用博弈论对认知无线电技术进行研究，其中的关键是如何将博弈论引入到相应算法的设计和分析中，找到算法的纳什均衡点[6]。因此在利用博弈论分析认知无线电的频谱分配问题之前，我们首先将所研究的问题抽象成博弈论问题模型，认知无线电中的频谱分配问题是关系到不同用户频谱策略选择的博弈过程，我们假设把频谱的分配等同于信道的分配，即信道分配问题可以建模成一个博弈的输出。在这个博弈过程中，参与者是认知无线电用户，他们的行动策略是对传输信道的选择，并且他们的效用和所选择的信道质量相联系。信道质量信息可由认知无线电用户通过在不同的无线频率上的测量来获得。那么，频谱分配问题的博弈论数学描述的一般形式如下：

这里N是参与者（选择某个信道来传输的认知无线电用户）的有限集，si是相对于博弈者i的策略集，定义S={s1，s2，s3，…，sn}是策略空间，则Ui:S→R是效用函数集。在博弈中的每一个博弈者i，效用函数Ui是博弈者i的策略si和当前其对手的策略集s-i的效用函数，这里si是博弈者选择的策略，s-i是其对手的策略。

由于博弈者均独立进行决策并且受到其他博弈者决策的影响，博弈结果分析的一个关键问题是判断对于自适应信道选择算法是否存在收敛点，且这个收敛点对于任何用户都不会偏移，也就是纳什均衡。

因此，对于博弈参与者的一组策略，当且仅当

时，这组策略即行动向量就是纳什均衡。如果这个纳什均衡点也是策略最优点，这样的算法就是我们所需要的。基于博弈论的认知无线电频谱分配模型将频谱分配问题中的各用户间竞争博弈过程用博弈论的方法进行了描述，使博弈论在认知无线电频谱分配问题上的应用成为可能，但是在具体设计基于博弈论的算法时，发现就网络结构而言，基于博弈论的算法比较适合于分布式网络，网络中各节点以协同合作的方式传递策略选择信息，以便于在下一个算法周期中对自身策略进行修改，从而实现自适应的策略收敛。此外，基于博弈论的频谱分配算法要求系统存在一个初始分配状态，博弈论算法根据不同的优化目标实现频谱的重新分配。

2.2 算法设计的目标

认知无线电中进行频谱分配的目标根据实际要求的不同而有所区别。例如以最大化系统吞吐量为目标、以最大化信道利用率为目标、以最小化系统总干扰水平为目标等。在文中假设频谱分配算法以最小化系统总干扰水平为目标，如果用信干比描述用户所受到的干扰情况，在接收机，关于发射机j的信干比可以表示为：

这里pi是发射机i的发射功率，Gij是发射机i和接收机j之间的链路增益，f（k，j）是表示由节点k到节点j的干扰方程，定义如下：

因此，使得系统总干扰水平最小即是使各节点用户所受干扰最小，而用户之间在同一频谱上的干扰是互相的，这正符合了博弈论研究问题的特征。在明确了算法设计目标后，如何选取适当的效用函数，从而运用基于博弈论的认知无线电频谱分配模型设计正确的频谱分配算法，是我们要致力解决的关键问题。

2.3 效用函数的描述

前文明确了基于博弈论的算法设计是以最小化系统总干扰水平为目标，那么如何将小区内各用户的干扰情况用效用函数进行描述便是接下来要关注的问题。这些效用函数刻画了用户对于某个特定的信道的性能。效用函数的选择不是唯一的，但必须选择对于某个特定的应用具有实际意义的，并且还要具有某些数学性质，也就是说效用函数的选择要保证频谱分配算法能够达到均衡收敛。通常仅考虑策略的参与者是自私用户的情况，用户基于在某个特定信道上感知到的其他用户的干扰级别来评估信道 。

效用函数U具体表达如下[3]：

在上面的定义中，P={p1，p2，p3，…，pn}是 N 个无线电用户的发射功率集合，S={s1，s2，s3，…，sn}是策略集合

效用函数U由两部分组成，第一部分是认知用户受到其它认知用户在相应信道上的干扰Id，第二部分是该认知用户对其它认知用户在相应信道上产生的干扰Io。

则可以得出效用函数U的另一个表达方式：

其中Id的值在用户接收端测量得到，而IO的值在用户发射端计算得出。通常在采用U效用函数的情形下，因为算法需要在公共控制信道上有一个数据包来传递用户对相邻节点干扰的测量信息，所以算法复杂度会增加。但是，效用函数U的设计能够反映最小化系统总干扰水平的总目标，只要每个用户的效用函数值达到最大即可。而对效用函数的博弈论分析，则是频谱分配问题模型的主要任务，论证效用函数纳什均衡的存在，讨论这样的纳什均衡是否满足需要，确定收敛的条件等，这样，就可以对相应的算法预测其收敛性，论证均衡状态的最优性[10]。一旦算法的效用函数确定，就可以针对效用函数的数学形式设计相关的信令协议，并搭建仿真平台进行仿真实验，验证仿真结果与算法的博弈论分析的一致性。

3 仿真结果讨论

在本算法中假设一个场景，在50×50 m2的区域内随机分配10个用户，假定初始时刻用户的发射功率在0～1 W之间，用户的最大发射功率为1 W，各用户随机分布在这个认知无线电小区内，一个收发机在同一时刻只能占用一个信道。初始时刻，将各信道分配给各个用户（算法中初始定义），开始时刻，通过执行一次算法确定取得竞争机会的用户在各个信道上的效用函数，并计算初始时刻的SIR，通过柱状图形显示，如图1所示，一次算法结束，记录一次结果，在初始值中设计算法共执行40次，记录每次的信道占用情况通过图形显示。

图1 算法执行前后的用户的SIR值对比Fig.1 Change of the user’s SIR value when performing the algorithm

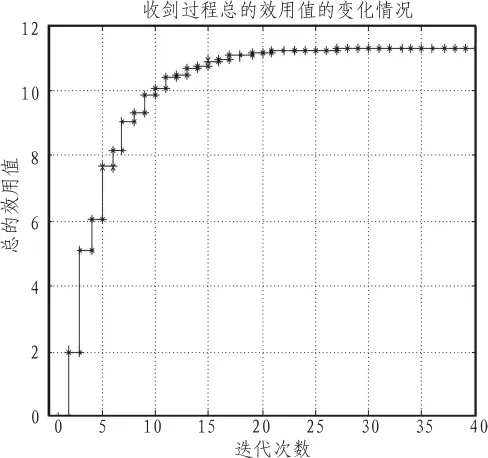
图2 算法执行过程中总的网络效用的变化情况Fig.2 Change of the net utility when performing the algorithm

则在整个小区中总的网络效用可以用式（10）来衡量。从图2仿真结果中算法执行前后各用户的SIR值对比可以看出，算法执行后各用户的SIR状况得到了明显的改善，整个系统的SIR水平得到了优化，仿真过程还测量了单个用户的SIR值，目的在于通过对比，验证以最小化系统干扰水平为目标的频谱分配算法有助于系统整体性能的提高。从图2的仿真结果可以看出随着算法执行过程的进行，整个小区的总的网络效用值在不断的增加，而增加到一定的程度，随后趋于稳定，此时各用户在其特定的信道位置上不再变化，系统达到一种使信道资源最大化利用的状态。

4 结 论

综上所述，利用博弈论设计认知无线电频谱分配算法，是一种行之有效的方法，理论上实现了灵活的频谱资源配置和工作状态调整。文中首先阐述如何利用博弈论对认知无线电进行分析，提出算法设计需要解决的4个方面的基本问题。在此基础之上进一步提出了基于博弈论的认知无线电频谱分配问题模型和算法设计的目标，并重点对模型中算法的收敛性及效用函数的选择做了详细的探讨和仿真，为以后更多基于博弈论的认知无线电频谱分配算法设计提供一定的参考。

[1]Mitola J，Maguire G，JR.Cognitiveradio:makingsoftwareradios more personal[J].IEEE Pers.Commun，1999，6（6）：13-18.

[2]Mitola J.Cognitive radio for flexible mobile multimedia communications[C]//IEEE.（MoMuC'99），1999:3-10.

[3]Haykin S.Cognitive radio:brain-empowered wireless com-munications[J].IEEE J.Select Areas Commun.，2005，23（2）：201-220.

[4]Buddhikot M M，Ryan K.Spectrum management in coordinated dynamic spectrum access based cellular networks[C]//Proc.IEEE DySPAN，2005：299-307.

[5]Neel J，Buehrer R M，Reed J，et al.Game theoretic analysis of a network of cognitive radios[C]//Midwest Symposium on Circuits and Systems，2002.

[6]Neel J.How Does Game Theory Apply to Radio Resource Management?[C]//In partial fulfillment of the requirements for qualification for acceptance to the Virginia Tech Doctoral Program，2002.

[7]WANGWei，LIUXin.List-Coloring based Channel Allocation for Open-Spectrum Wireless Networks[C]//In Proc.of IEEE VTC，2005：690-694.

[8]ZHENG Hai-tao，PENG Chun-yi.Collaboration and fairness in opportunistic spectrum access[C]//Proc.IEEE ICC 2005，2005：3132-3136.

[9]徐友云，高林.基于步进拍卖的认知无线电网络动态频谱分配[J].中国科学技术大学学报，2009，39（10）：1604-1609.XU You-yun，GAO Lin.Dynamic spectrum allocation in cognitive radio networks based on multi-auctioneer progressive auction[J].Journal of University of Science and Technology of China，2009，39（10）：1604-1609.

[10]Werbach SK.The End of Spectrum Scarcity[J].IEEE Spectrum，2004，41（3）：48-52.