一种多约束条件下路径规划算法研究

李汉轩，李志华，吕春生

（1.河海大学 控制理论与控制工程系，江苏 南京 211100；2.91656部队 质量控制室，上海 200136）

目前，在最短路径规划方面，已经出现很多成熟优秀的算法。熟知的有Dijkstra算法、Ford算法，以及启发式的A*算法。这些算法在路径规划中对于解决只有距离限制的点与点之间最优路径的问题有着良好的时间复杂度[1]。在实际的车辆导航系统中，往往用户更希望能得到一些带约束条件的路径规划。在多约束条件的路径规划研究中，目前的确定性解决方法都拥有较高的时间复杂度[2-3]。而遗传算法、蚁群算法是近年来迅速发展起来的基于生物进化原理的全局性优化算法，在解决多约束路径规划问题中取得了很大成效[4-5]。这种仿生学算法往往具有良好的鲁棒性，并有着并行，反馈等特点，但收敛性不强，可能会陷入局部最优，无法得到全局最优解。文中结合A*算法和蚁群算法优点，提出了一种新的不确定算法。

1 基本算法

1.1 A*算法分析

A*（A-Star）算法是一种静态路网中求解最短路最有效的方法。如图1所示，算法中，将目前位置与目标位置的欧氏距离作为评估值，通过选择最小路径评估值，不断回溯运算，可求出全局最短距离。

公式表示如式（1）。

其中，f（n）是从初始点经由节点n到目标点的估价函数，g（n）是在状态空间中从初始节点到n节点的实际代价，h（n）是从n到目标节点最佳路径的估计代价。

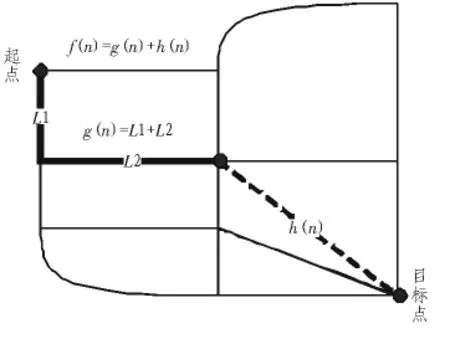
图1 A*算法评估值示意Fig.1 A*algorithm assessed value

1.2 蚁群算法分析

蚁群算法（Ant Colony Optimization， ACO），又称蚂蚁算法，是一种用来在图中寻找优化路径的机率型技术。它由Marco Dorigo于1992年在他的博士论文中引入，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。概率转移函数如式（2）所示：

式中:Pk（r，s）表示蚂蚁k从节点r转移到节点 s的概率；τ（r，s） 表示蚂蚁储存在边 V（r，s） 上的生物信息激素强度；η（r，s） 表示节点 s 相对于节点 r的可见性，η（r，s） =1/crs，crs表示边 V（r，s） 的代价；Jk（r） 是第 k 个蚂蚁由节点 r可以到达的所有可行节点集合。

蚁群算法在路径规划问题中往往根据两节点间的距离和信息素浓度作为节点转移的参考。不能考虑下个节点和目标点关系的信息，导致在寻优过程中收敛性不高。

2 多约束条件下的路径规划算法

在实际路径规划时，往往面临多个约束条件的限制[6]。文中提出一种路径代价指标，将所有约束条件加权融合，使多约束问题转化为单约束问题。同时利用A*算法的评估值概念，引入预测代价概念为蚁群在路径选择时提供额外的信息来源，最终用加权的路径代价和加权的预测路径代价作为一种广义的路径代价指标，基于这种思想，本文提出了基于A*和蚁群算法融合的新算法。对多约束条件的加权融合方法如式（3）。

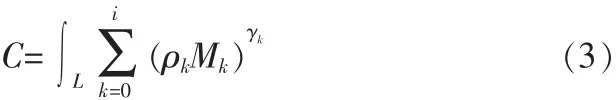
其中L是道路长度，ρ是权重系数，γ是转移因子，M为代价均值。其中转移因子γ的作用是在用户设定完约束意愿后，系统可以根据系统状况作动态的改变规划路径。文中对导航系统的路径模型作一定简化，将影响路线规划的道路条件设定为路线长度，路线宽度，路线材料3种。

距离在上述路径代价指标中虽然不能完全决定多约束路径的方向选择。但在一般导航中距离都是重要的因素。所以利用A*算法中的评估值概念 （即节点与目标点的欧氏距离），为路径规划引入预测代价概念-欧式距离。将欧氏距离作为蚂蚁在路径选择的额外“信息素”，加上蚁群算法本身的机率性可以实现快速、全局的最优路径选择。

2.1 节点寻找

根据文中提出简化路径模型，参考代价指标公式，融合多约束条件后的新的转移预测代价可以表示为：

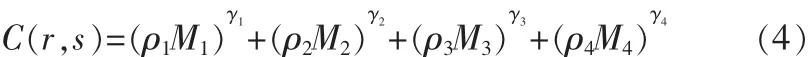
式中: （ρ1M1）γ1表示 r节点到 s节点的路线距离指标，（ρ2M2）γ2

表示 r节点到目标结点的路线材料指标，（ρ3M3）γ3表示路线宽度的指标，（ρ4M4）γ4表示预测代价指标。

根据（2）式与（4）式，新的转移公式如下：

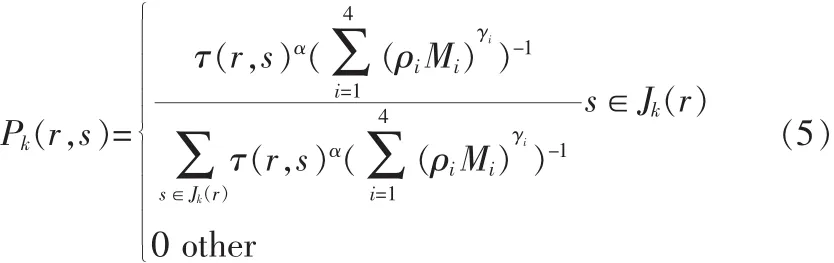
2.2 节点转移

文中采用J.H.Holland教授提出的轮盘方式选择转移目标结点[7]，它是一种按转移概率大小随机选择优良目标的方法。目标被选择的概率取决于目标转移概率的大小，即：

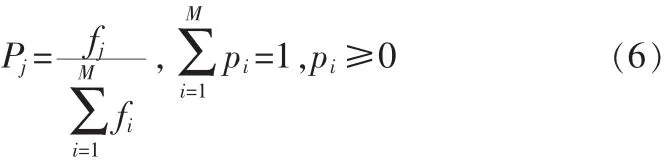
式中：Pj为目标j被选中的概率；fi为个体j的转移概率；M为群体中个体的数目。故fi越大，Pj也就越大，则该目标被轮盘选中（择优时）的可能性就越大。

2.3 算法设计与实现

在算法实现时，参照文献[2]设计了图的存储结构，具体流程如图2所示。

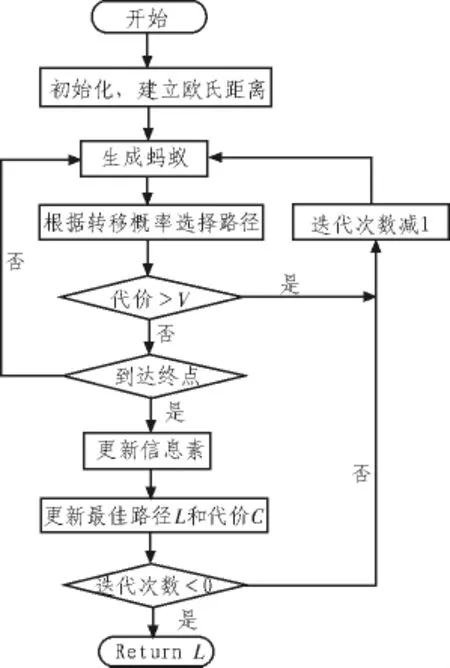
图2 A*与蚁群结合算法流程Fig.2 Flow chart of A*combined with ant colony algorithm

步骤1：建立图形中个顶点到目标顶点的欧氏距离及其他代价值；

步骤2：生成一个蚂蚁，从起点开始出发根据信息素浓度和预测转移概率选择路径；

步骤3：根据蚂蚁的路径，更新信息素，记录最优路径。

重复2、3步至迭代次数完成。

3 仿真结果

文中实验时，根据截取的河海大学附近地图制作了简化图如图3所示 。截选地图有28个顶点，46条边。本次路径共假定3种约束条件分别为路线长度，耗费时间，所经过的道路材料。其中在路况中将道路拥挤度分为4级，从1级到4级拥挤度逐渐增加。具体路线拥挤如表1所示：将道路材料分为3种包括柏油或水泥路面，沙砾路面，土路如表2所示。根据本次实验的驾驶意愿，3种约束条件在融合过程中的权重因子分别为：路线长度0.6，道路拥挤度0.2，道路材料0.4。转移因子均为1。实验结果如表3所示。

表1 路线拥挤表Tab.1 The extent of line crowding

表2 路线材料表Tab.2 Line materials

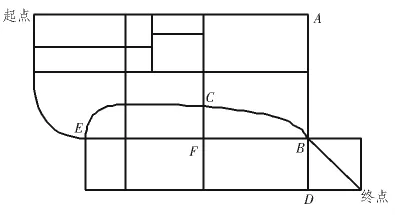
图3 简化抽象拓补结构图Fig.3 Simplify figure of the abstract topology

由于蚁群算法运行结果的随机性，单次算法运算的结果不能客观反映方案的优劣，该研究共进行了5轮测试，每轮生成100只蚂蚁最多迭代50次的统计值作为比较。

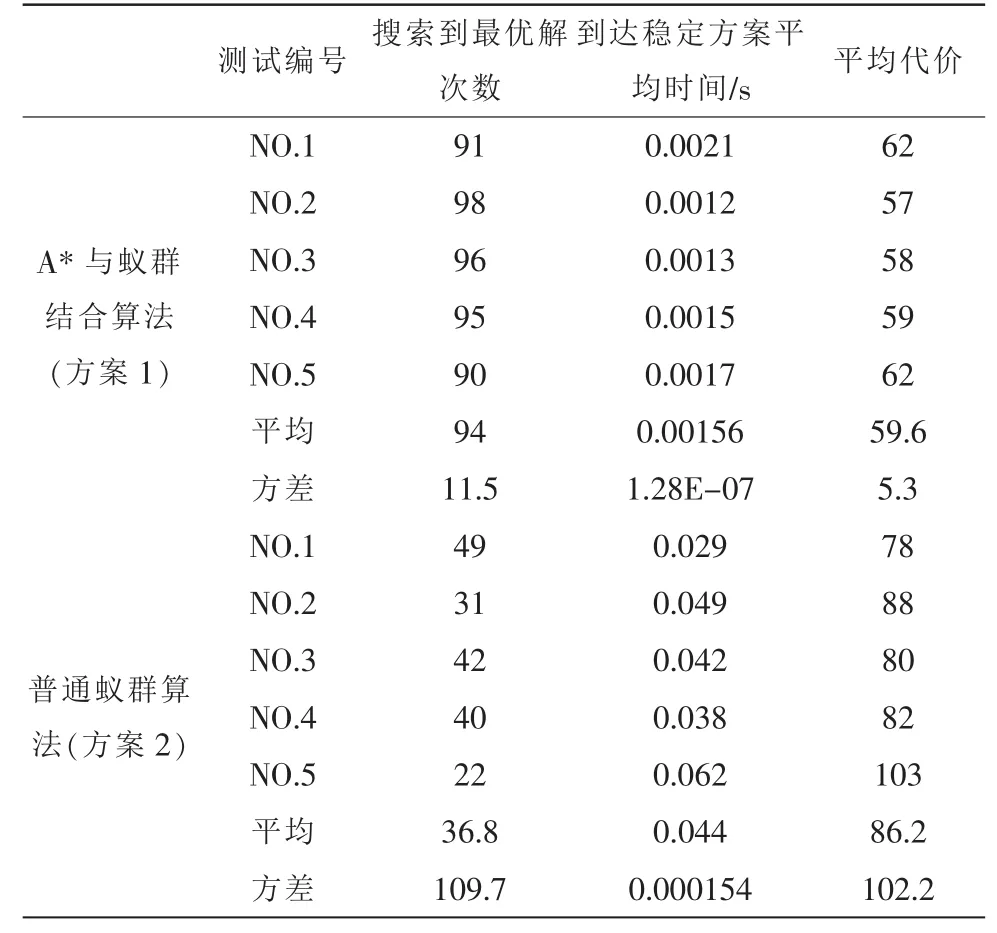
表3 测试结果Tab.3 Test result

1）在每轮实验中均采用了大样本实验，即5轮测试共进行5×100次路径寻找运算，进行实际运算测试。从各项统计指标的绝对值及其方差来看，在同种方案内的不同测试中统计数据项结果波动很小；

2）方案1的总运行时间明显缩短（仅为前者的3.55%），方案2的总运行时间大部分被无效路径选择占用，其原因是常规蚁群算法有效信息素积累慢，收敛性不强导致；由于是在同一软硬件平台上进行方案测试，故统计数据具有可比性；

3）两方案的搜索最优解次数（即每轮大样本实验中算法停止时的寻优解为全局最优解的次数）相差2.55倍，说明2方案除了在速度上的明显差异外，在全局最优解的搜索成功率上也是效果明显不同的；

4）由于欧氏距离因子可以为路径选择做出非常有效的方向预测，进而提供稳定的最优路径获取成功率。所以方案1的最优解次数方差远远低于方案2，证明改进方案在获得全局最优解能力方面有着很好的稳定性。

4 结束语

文中提出了一种基于A*算法和蚁群算法融合的多约束条件最优路径导航算法，能够保证在路径规划时得到一条具有较小行驶代价的航路。可以看出，这种路径规划方法具有如下特点：1）保留了蚁群算法具有的动态性，分布性，协同性；2）加入A*算法的估计代价因子增加了算法的收敛速度，算法也更容易更稳定的得到全局最优解。

[1]严寒冰，刘迎春.基于GIS的城市道路网最短路径搜索算法[J].计算机学报，2000， 25（3）:210-215.YAN Han-bing，LIU Ying-chun.A new algorithm for finding shortcut in a city’s road net based on GIS technology[J].Chinese J.Computers，2000，25（3）:210-215.

[2]戴树贵，潘荫荣，胡幼华，等.求带多个限制条件的单源多权最短路径算法[J].计算机应用与软件，2004，21（12）:78-81.DAI Shu-gui，PAN Yin-rong，HU You-hua，et al. An algorithm for the multiple weights shortest-path problem with multiple constraints[J].Computer Applications and Software，2004，21（12）:78-81.

[3]Takaoka T.An O （n3loglogn/log n）time algorithm for the allpairs shortest path problem[J].Information Processing Letter，2005，96:155-161.

[4]Dorigo M，Gambardella L M， Middendorf M，et al.Guest editorial:special section on ant colony optimization[J].IEEE Transactionon Evolutionary Computation，2002，6（4）:317-319.

[5]柳长安，李为吉，工和平.基于蚁群算法的无人机航路规划[J].空军工程大学学报，2004，5（2）:9-12.LIU Chang-an， LI Wei-ji， GONGHe-ping.Path planning for reconnaissance UAV based on ant algorithm[J].Journal of Air Force Engineering University，2004，5（2）:9-12.

[6]王海梅.基于GIS的最优路径算法研究与实现[D].南京:南京理工大学，2008.

[7]HUANG Kai-ming.Analysis and improvement on roulette wheel method of genetic algorithm[J].Computer Engineering and Applications，2009，45（28）：60-63.