超空泡水下航行器直航弹道三通道控制与动态特性仿真

李雨田，张宇文，李代金

(西北工业大学 航海学院，西安 710072)

超空泡水下航行器处于直航巡航时，以超空泡技术为支撑有效地降低了流体阻力，同时由于航行器表面大部分被空泡包覆，使得其运动模式有别于常规的全沾湿水下航行器，运动特性也表现出独有性。由于受到空泡的扰动、发动机推力偏心造成的震荡以及超高速带来的流体动力改变的影响，超空泡航行器直航弹道的稳定性会有所降低。在此情况下研究直航弹道的稳定控制是超空泡水下航行器诸多研究环节中重要的一环。

在对超空泡水下航行器的研究中，国内外学者针对其控制方式提出不同的研究方案。文献［1］采用非线性反馈线性化的方法对超空泡航行器的非线性数学模型进行处理;文献［2］应用最优控制方法对超空泡航行体的运动控制器进行设计;在文献［3］中，学者研究了超空泡航行体纵向运动的基准问题，采用线性化方法研究了超空泡航行体纵向运动的稳定性控制;在文献［4-5］中，学者对超高速水下航行器的航向和纵平面姿态进行了控制方法的探讨;文献［6-7］基于变结构理论提出了自适应变结构和自适应滑模的控制方式实现对航行器的稳定控制。

本文在前人研究的基础上，采用空化器首舵和航行器尾舵实施对航行器俯仰、偏航和横滚三通道的控制，利用极限操舵的方式实现各通道间的解耦，实现超空泡水下航行器直航弹道的稳定控制。

1 超空泡航行器流体动力布局

1.1 定义坐标系

研究超空泡水下航行器直航弹道采用的坐标系为地面坐标系O0X0Y0Z0和雷体坐标系OXYZ［8］。地面系用于描述弹道轨迹和弹道坐标，雷体系便于分析航行器三通道航行姿态及运动控制。

1.2 超空泡航行器三通道流体动力分析

(1)纵平面流体动力分析

超空泡航行器纵平面主要受到三个力的作用:航行器质心处的重力G、航行器头部空化器的升力Yk、航行器后体的升力Yb。如图1所示，为超空泡航行器三通道受力示意图。

(2)水平面流体动力分析

图1 超空泡航行器三通道受力Fig.1 Forces acting in three-channel of a Supercavitating Vehicle

超空泡航行器水平面主要受到两个力的作用:航行器直舵产生的侧向力Zd;作用在航行器后体的侧向力Zb，水平面受力如图1所示。其中Zb主要由侧滑角β以及角速度ωy产生。

(3)横滚流体动力分析

超空泡航行器以旋转角速度ωx转动时形成的附加阻尼力矩，其产生的机理主要是存在ωx时，航行器表面附体(上下直舵)处出现附加攻角从而附加产生阻尼力矩 Mxω:

1.3 超空泡航行器直航弹道空间运动模型

综合超空泡航行器相关流体动力的分析，参照常规全沾湿航行器空间运动方程的研究方法［9］，简化得到常规流体动力布局的超空泡水下航行器的空间运动方程如下:

其中，描述重心运动的6个弹道参数:航速v、弹道倾角Θ、弹道偏角Ψ和运动轨迹的3个分量x，y，z;以及确定航行器转动的6个姿态参数:俯仰角θ、偏航角ψ、横滚角φ和这 3 个姿态角的角速度ωx、ωy、ωz;Jx、Jy、Jz分别描述了绕航行器 X，Y，Z轴的转动惯量，Axv2描述了航行器阻力。

2 基于极限操舵模式的三通道控制

超空泡水下航行器姿态角对于系统干扰以及控制作用的响应［10］非常快而且增益非常大，除了在控制算法中突出超前环节以外，对于控制执行机构的快速性要求也非常高，考虑到控制执行机构(舵机系统)的响应特性，简化起见，本文对操舵控制采取两位极限操舵模式进行航行器的三通道控制。

对空化器的偏转控制实施两位极限操舵模式，其平衡舵角位置应在运动中位，操舵幅度的大小取决于平衡舵角预估值的准确性。平衡首舵角预估值愈准确，操舵幅度愈小，航行器运动愈平稳。又为了维持航行器的受力平衡，航行器的平衡攻角必须为正，如此才能产生正升力与重力平衡;同时为了保持力矩平衡，就必须有相应的平衡舵角。平衡攻角不宜过大，否则会增加阻力。平衡舵角则是越小越好，否则舵角的有效变化范围将减小。另外，操舵频率和控制算法的死区设置也影响系统运动的平稳性，操舵频率高，平稳性好。

2.1 纵平面通道控制算法

纵平面内，深度俯仰角控制实施控制算法如下:

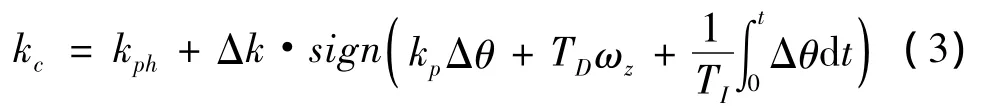
其中，kp、TD、TI分别为比例增益、微分时间和积分时间;kc、kph、Δk分别为指令首舵角、平衡首舵角和舵角变动量;Δθ为俯仰角偏差。为了减小定深控制造成的系统深度偏差，期望俯仰角可以设定为平衡攻角的估计值，Δk的大小取决于kph预估值的准确性，至少应使实际的平衡攻角在kph±Δk之间，当然，kph值是随着推进剂的消耗而逐渐变小的。另外，由于控制过程中不允许出现|α| ＞αs的情况，考虑α对k的振荡响应特性，设系统阶跃响应的超调量为φ、α对于k的响应增益为kkα、平衡攻角为αph，则Δk的限制关系可写为:

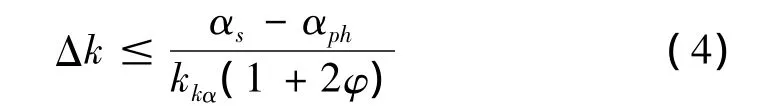
2.2 水平面通道控制算法

水平面内为航向控制通道，航行控制算法为:

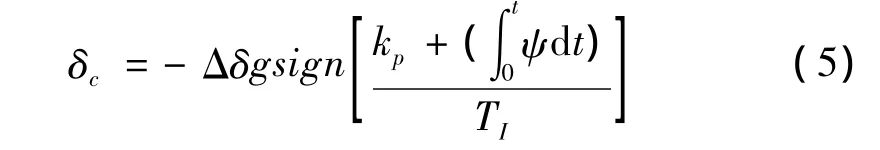
其中:δc、Δδ分别为指令舵角和舵角极限量。由于控制过程中不允许出现|β| ＞βs的情况，考虑β对于阶跃(的振荡响应特性，设系统β对于阶跃(的超调量为φ、增益为kδβ，则Δδ的限制关系为:

由于Δδ的限制，理论上，当发动机推力偏心很大时，可能出现控制作用不足的现象。但是从发动机制造、安装的具体工艺水平来看，由于推力偏心量有限，舵角量值不会太大，将小于式(6)给出的舵角限制值。

2.3 横滚通道控制算法

对于横滚通道，经两位极限操舵模式控制的横滚通道其响应也是振荡的，只要振荡幅度不很大，其效果也是可以接受的。横滚通道的控制算法为:

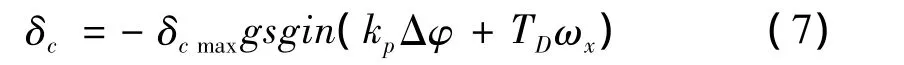
其中:δc、δcmax分别为指令空化器与抗横滚差动舵角和舵角极限量。考虑到控制作用与干扰作用的量值关系，δcmax的选取是关键的，量值过小不足以对抗直舵的不平衡流体动力，选取过大则会引起横滚振荡过程的幅度过大。

3 弹道动态特性仿真与分析

以上述建立的适用于超空泡航行器直航弹道的空间运动模型作为控制系统的仿真模型，综合纵平面、水平面和横滚三通道极限操舵模式控制规律，对航行器直航弹道的系统动态特性进行仿真。

3.1 仿真条件

针对直航弹道规划进行仿真计算。仿真参数如下:

(1)控制系统参数:舵机极限舵角转换时间60 ms，期望俯仰角 0°，期望偏航角为 -45°，期望横滚角 0°;

(2)仿真步长:1 ms;(3)仿真时间:10 s;

(4)仿真内容:设定航行器出管速度50 m/s，初始横滚角25°;主动段自模型出管起算8s(发动机在模型出管后8 s停车)。

3.2 仿真结果及其分析

超空泡航行器纵平面的运动仿真如图2(a)、图2(b)、图2(c)和图2(d)所示。

由纵平面的运动仿真曲线可以看出:随着空化器首舵在纵平面内的偏转控制，没有出现攻角过大的现象，如图2(a)所示，其根源在于俯仰角间接控制规律综合时考虑到攻角对空化器首舵角的阶跃响应震荡特性，对Δk实施了限制。由图2(b)、图2(c)可以看出，基于航行器运动平稳性的考虑，航行器运动过程中配置的操舵频率较高，操舵频率越高，运动平稳性越好。航行器的俯仰角速度、俯仰角，连同攻角与首舵角的跟随性良好，系统的动态特性良好。深度偏差在整个航行过程中有些微振荡，但幅度不大，如图2(d)所示，其振荡、超调均在可接受范围。说明采用深度间接控制(俯仰角控制模式)，对高航速航行器巡航段实施控制是适用的。

图2 航行器纵平面动态特性仿真Fig.2 Vertical plane characteristic simulation of vehicle

图3 航行器水平面动态特性仿真Fig.3 Horizontal plane characteristic simulation of vehicle

超空泡航行器水平面的运动仿真如图3(a)、图3(b)、图3(c)和图3(d)所示。

从水平面的运动仿真曲线可以看出:在航向通道的控制规律综合中由于对Δδ实施了限制，也没有出现侧滑角过大的情况，由图3(a)所示。从图3(b)、图3(c)可以看出，偏航角、偏航角速度与空化器首舵的水平偏转跟随性良好，且可以稳定在期望值附近，航向通道特性可以得到保证。如图3(d)所示，偏航角可稳定维持在期望值-45°附近，弹道水平偏移量变化平稳，偏差小，几乎无振荡。

超空泡航行器横滚通道的仿真如图4(a)、图4(b)所示。

图4 航行器横滚动态特性仿真Fig.4 Roll characteristic simulation of vehicle

从横滚通道的控制图4(a)、图4(b)可以看出，在初始横滚角为25°的条件下，横滚控制系统控制角速度及横滚角略微有振荡，但振荡幅度可以接受，横滚角最终稳定到期望值0°附近，横滚角、横滚角速度与附加抗横滚舵舵角的跟随特性良好，控制效果满足系统的要求。

3.3 自主航行试验

为了验证控制算法的可行性进行了超空泡水下航行器外场自主航行试验，目标要求航行器实现稳定直航，采用极限操舵的三通道控制方法。图5所示是采用固定摄像机实际拍摄获得的直航弹道航迹。直航段超空泡形态是通过水下高速摄像系统获取，其超空泡形态如图6所示。

根据稳定自主航行控制试验数据，解读模型内部测控系统记录的数据，得到超空泡航行器直航弹道三维示意图，如图6所示。

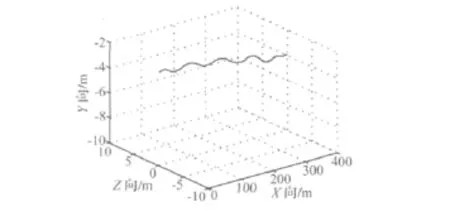
图7 试验直航弹道解读图Fig.7 Trajectory of experimental results

图7 实验信号阶数选择及滤波分析结果Fig.7 Order selection and filtering analysis of experimental signal

4 结论

本文通过AR预测滤波器对滚动轴承故障诊断中降噪性能的研究，详细讨论了AR预测滤波器在轴承故障诊断中的阶数选择问题，揭示了其最优阶数选择与轴承的信噪比、衰减阻尼比、采样频率和结构共振频率之间的关系，提出了基于McFadden模型的衰减信号整周期截取准则，同时进一步利用峭度最大化原理给出AR预测滤波器的最优阶数参考。

［1］McFadden P D，Smith J D.Model for the vibration produced by a single point defect in a rolling element bearing［J］.Journal of Sound and Vibration，1984，96(1):69-82.

［2］ Dron J P，Rasolofondraibe L，Couet C，et al.Fault detection and monitoring of a ball bearing benchtest and a production machine via autoregressive spectrum analysis［J］.Journal of Sound and Vibration，1998，218(3):501-525.

［3］Marple L.New autoregressive spectrum analysis algorithm［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，1980，28(4):441-454.

［4］ Cheng J S，Yu D J，Yang Y.A fault diagnosis approach for roller bearings based on EMD method and AR model［J］.Mechanical Systems and Signal Processing，2006，20(2):350-362.

［5］张海勇，李 勘.非平稳随机信号的参数模型分析方法［J］.系统工程与电子技术，2003，25(003):386-390.

［6］徐 峰，王志芳，王宝圣.AR模型应用于振动信号趋势预测的研究［J］.清华大学学报，1999，39(004):57-59.

［7］ Akaike H.Fitting autoregressive for prediction［J］.Ann.Inst.Math，1969，21:243-247.

［8］ Akaike H.A new look at the statistical model identification［J］.IEEE Trans.Autom.Control，1974，19:716-723.

［9］ Broersen P M T，Wensink H E.On the penalty factor for autoregressive order selection in finite samples［J］.IEEE Transactions on Signal Processing，1996，44(3):748-752.

［10］ Thanagasundram S，Schlindwein F S.Autoregressive order selection for rotating machinery［J］.International Journal of Acoustics and Vibrations，2006，11(3):144-154.

［11］ Endo H，Randall R B.Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter［J］. Mechanical Systems and Signal Processing，2007，21(2):906-919.