半主动变刚度TLCD减振控制的研究

霍林生，李宏男

（大连理工大学 海岸与近海工程国家重点实验室，大连 116024）

作为动力吸振理论在结构控制工程中的应用，调谐质量阻尼器（Tuned Mass Damper，TMD）和调谐液体阻尼器（Tuned Liquid Damper，TLD）取得了一定的成功，均不乏工程实例。作为 TLD的一种变例，Sakai［1］提出了U型液体调谐阻尼器TLCD（Tuned Liquid Column Damper）减振控制装置，其构造为一内部充液（通常是水）的U型管状刚性容器，水平管道中部设有预留孔。通过调谐管内液柱的振动频率至接近或等于结构的固有频率并选定适度的液力阻尼，然后附于结构之上，则结构的部分运动能量将传递给液体，引起液柱的振动，从而改善结构的动力状态。

TLCD中通常会装设开有小孔的隔板，液体在流经小孔前后，由于截面突然变化，运动的液体将会产生局部水头损失，这种损失是 TLCD耗散能量的主要部分［2-6］。因此，TLCD减振系统的阻尼是通过液体流经预先设置的孔洞产生的，但是孔洞引起的阻尼力是内在非线性的。对于这种非线性系统，TLCD如何确定合适的液力阻尼是一个不易解决的难题。尽管在一些文献中建议采用等效线性化技术处理非线性阻尼，但由于这种等效线性阻尼依赖结构动力响应，以致优化阻尼条件不能在一个较广的范围内成立，带有很大的局限性。因此虽然隶属于被动控制系统的TLCD可以发挥一定的作用，但其有效性是有限的。为了克服被动控制系统的限制，相应地出现了一种对应于TLCD的半主动控制装置［7-13］，即 SAVD-TLCD（Semi-active Variable Damping Tuned Liquid Column Damper），如图 1所示。SAVD-TLCD可以根据既定算法，实时调整开孔率，以适应不同时刻阻尼的需要，并保留了TLCD的主要优点。理论分析和实验研究显示这种控制系统能在被动控制的基础上进一步减少结构的振动。

U型管中液体振荡的频率与液体的长度有关，当结构的自振频率较高时，在不影响使用的条件下，很难将液体的自振频率调节到与结构的自振频率相等或接近，从而影响了TLCD的减震效果。阎石等［14］提出了在U型阻尼器上设置调频系统（图2），使液体的振荡频率可以调节，从而增加了TLCD的应用范围。但是，这种可调频TLCD所附加的弹簧系统的刚度在控制过程中是不可改变的，因此TLCD减振系统的频率也是保持不变的。由于TLCD控制的原理是通过液体的振动来吸收结构振动的能量以降低结构的动力反应，但是在结构振动过程中，外部环境作用（如地震和风）的频谱特性在不同的时段是不同的，因而在每一时刻，TLCD对结构的控制作用并不是最优的。为改进被动式调频TLCD的减振特性，本文基于半主动控制的概念提出了半主动变刚度TLCD减振系统（Semi-active Variable Stiffness Tuned Liquid Column Damper，SAVS-TLCD），如图3所示。这种新型半主动变刚度TLCD基本原理是将调频TLCD的弹簧设置成可调谐状态，在振动过程中，根据减振系统的需要适时调整TLCD的频率，以获得更好的减振效果。借鉴日本学者Kobori［15］研制开发的主动变刚度AVS（Active Variable Stiffness）装置，变刚度TLCD附加调频系统的刚度可适时切换，如图4所示。该装置由弹簧、液压缸、活塞和阀门组成。当阀门处于关闭状态时，液体不可压缩，该装置能向系统提供一定的刚度。当阀门处于打开状态时，活塞在液缸中可以自由装置不能提供刚度。需要指出的是，尽管主动变刚度装置中的液压路确实存在阻尼，但该装置提供的阻尼力同弹簧提供的恢复力相比一般很小，因此在计算中不考虑变刚度装置的阻尼力。

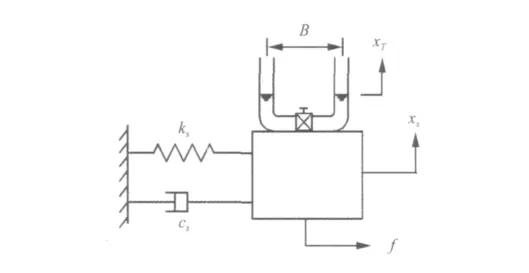
图1 半主动变阻尼TLCDFig.1 Semi semi-active variable damping TLCD

图2 可调频TLCDFig.2 Frequency adjustable TLCD

1 半主动变刚度TLCD的减振性能

1.1 变刚度TLCD运动方程

设结构水平方向的位移为xs，在U型管的两端各附加一个刚度为kT2的弹簧，其中弹簧的刚度kT2在振动过程中是可调的，如图3所示。假定液体在运动过程中内部能量保持不变，由Lagrange方程建立液体的运动方程如下：

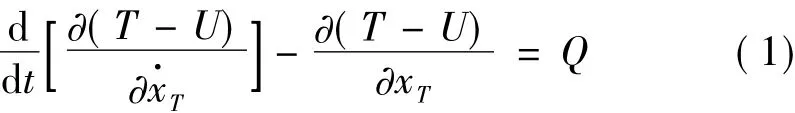
式中：xT为液体在振动过程中离开平衡位置的距离；T、U分别为液体运动时的动能和势能。液体振荡的动能可由下式确定：

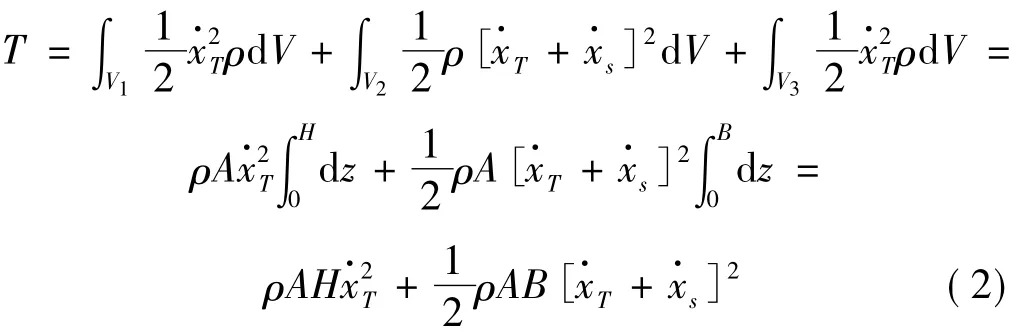
式中：A为U型管的横截面积；ρ为液体的密度；H为静止时，两竖管中液体的高度；B为两竖管的中心距；xs为安装TLCD的结构的位移；V1、V3代表U型管的竖向部分，V2代表水平部分。液体的势能U可以表示为：

式中：g为重力加速度；z为积分单元距水平管轴线的距离；kT2为附加的可变弹簧的刚度。将非保守力Q表示为液体流经小孔时局部水头损失系数ξ的函数，由水头损失的定义可得：

分别将式（2）、式（3）和式（4）代入式（1），可得到液体的运动方程如下：

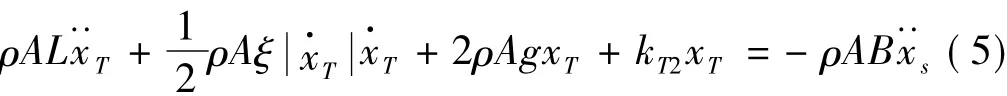
在不加调频装置时，对于自振频率较高的结构，为达到使液体的自振频率与结构的自振频率相等的目的，液体的长度很短，有时影响TLCD的使用。设置调频装置后，可以通过调节附加弹簧刚度的方法来调节TLCD的频率，从而拓宽了TLCD的应用范围。

对于被动式调频TLCD装置，液体振动过程中附加刚度系统的弹簧刚度kT2是保持不变的，但是对于半主动变刚度TLCD减振装置，kT2根据控制系统的需要是适时变化的。振动过程中，变刚度装置的阀门分为“开”和“关”两种状态，相应地附加刚度系统kT2的值为：

其中：k0为变刚度装置中弹簧的刚度，如图4所示。

由于式（5）中阻尼系数是非线性的，为简化计算，采用等价线性化的方法将液体运动时的阻尼系数线性化。将方程（5）改写为：

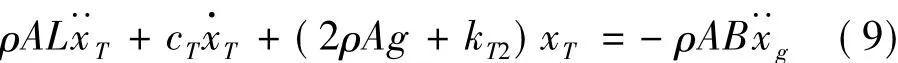
式中：cT为等价线性阻尼系数。如果为零均值平稳Gauss随机过程为的标准差，则cT可表示为［9］：

1.2 半主动控制策略

设置半主动变刚度TLCD后的受控结构的运动方程可表示为：

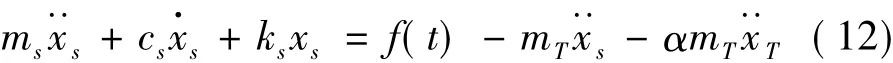
从上式右边可看出，液体相对于结构运动施加影响共有两项，分别记为：

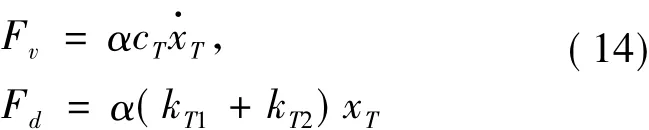
两者均具有力的量纲。Fv性质上为一种液动阻力，与TLCD的阻尼系数cT有关；而Fd与TLCD的刚度有关的恢复力。两者都是因为液体相对结构运动而施加于结构之上，在每一瞬时对结构的动力响应均有影响。对于半主动变刚度TLCD，调节阀门的开关可以瞬时改变刚度系数kT2，因此，在整个动力响应过程中，通过考察Fd对结构振动的影响，采取适当的控制策略，不断调整阀门的“开-关”状态以实现Fd对结构最优控制，最有效地抑制主体结构的反应。杨润林［16］根据结构在围绕平衡点附近一个往复运动的划分，提出了一种离复位（OTE）控制策略，可以适用于主动控制和半主动控制。本文的研究中，采用这种控制算法。

根据OTE策略，就SAVS-TLCD的半主动振动控制而言，液体振荡过程中对结构的控制力并不总是有利的，需要结合结构的运动过程考虑：如果结构（楼层）远离平衡位置，应该调整控制力抵抗结构（楼层）的运动；如果结构（楼层）趋于平衡位置，应该调整控制力尽可能削减结构（楼层）的零位置穿越速度，以避免对下一往复运动的不利影响。在后一运动过程中，考虑到复位的需要，一个适度的复位速度也是必需的，因此采取适度抑制的方法是恰当的。由于TLCD对结构提供的控制力也与结构的响应有关，并且不足以超越激振力引起反向振动，因此可以选择如下的控制策略：在离位过程中，如果结构位移和控制力Fd同向，应该打开变刚度装置的阀门，这时弹簧可以自由滑动，不提供刚度；反之，如果结构位移和Fd反向，一个大的控制力对减小系统反应是有利的，因此变刚度装置的阀门应该关闭，这时变刚度装置提供刚度。在复位过程中，如果结构的位移和控制力Fd同向，变刚度装置就提供刚度；反之，如果结构运动和控制力反向，应打开变刚度装置的阀门，不提供刚度。根据OTE算法，双态离散控制的控制条件如下：

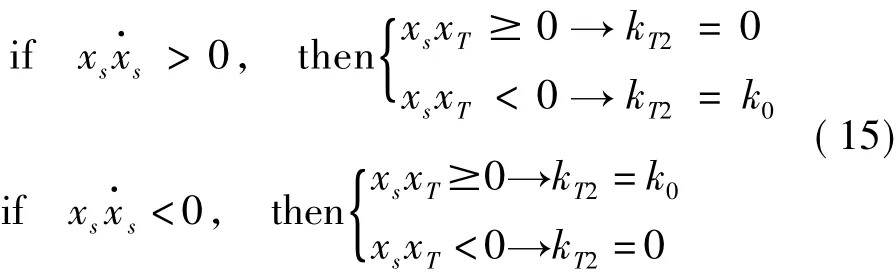
2 单自由度数值算例

本节通过一个单自由度的数值算例来分析半主动变刚度TLCD的减振作用。选用Haroun的算例［7］，结构的质量为ms=1.49×107kg，刚度为ks=1.49×107N/m，阻尼为cs=2.97×105N·s/m。TLCD中的液体采用普通水，水与结构的质量比μ=mT/ms=0.02。

首先按照被动式TLCD设计得到它的最优频率为ωT=0.989 2 rad/s，定义kT为：

其中：kT2为可变刚度装置提供的刚度，它的取值可以为0或k0。令：

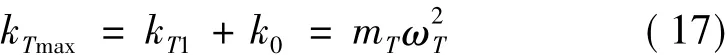
由上式可看出，SAVD-TLCD减振系统的刚度由两部分组成，一部分是TLCD的液体振动的恢复力部分kT1，另一部分是变刚度装置的弹簧提供。当变刚度装置的可变刚度k0越大，则TLCD的振荡提供的刚度kT1越小，相应地液柱的长度越长。下面首先分析k0的取值对控制效果的影响。定义位移减振率Jd和加速度减振率Ja分别为：

其中：下标unco和co分别表示未控结构的反应和控制后结构的反应。SAVD-TLCD的宽长比α取不同的值时，位移减振率Jd和加速度减振率Ja随k0/kTmax的变化曲线如图5所示。由图可看出，k0/kTmax的值越大，位移和加速度的减振效果越好。因此，在SAVD-TLCD的液柱长度满足使用功能和安装空间的条件下，变刚度装置的可变刚度k0值越大，系统的反应减小越多。

取kT1=k0=0.5kT，外荷载为p（t）=F［3sin（pt）+7sin（2pt）+5sin（3pt）+4sin（4pt）］形式，其中F=3.54×104N，p=1.0 rad/s。分别计算结构在无控、被动控制、半主动变阻尼控制和半主动变刚度控制情况下结构的反应，如表1所示。由表中的数据可知，同SAVD-TLCD一样，SAVS-TLCD同样对结构反应起到了很好的减振效果。同被动TLCD相比，SAVS-TLCD对结构位移和加速度反应的减振率在被动控制的基础上又增加了约20%。

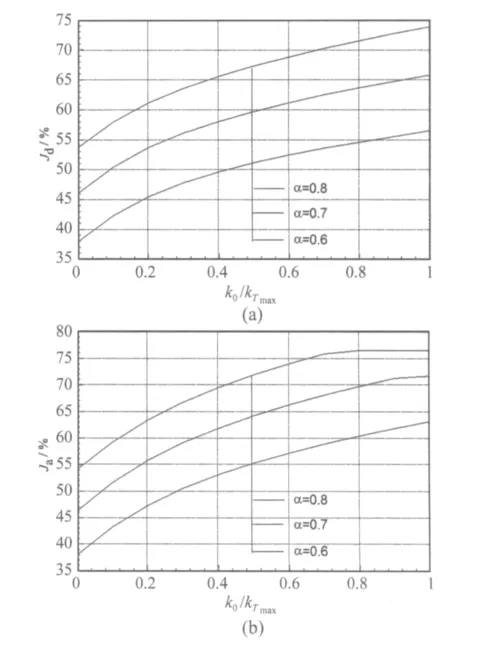
图5 Jd和Ja随k0/kTmax的变化曲线Fig.5 The curves of Jd和 Jawith k0/kTmax

表1 控制方案比较Tab.1 The comparison of control scheme

图6给出了在荷载激励下，结构未控、被动TLCD控制和半主动变刚度TLCD控制后的位移反应的时程曲线。图7给出了结构未控、被动TLCD控制和半主动变刚度控制下结构加速度反应的时程曲线。由图可看出，在时域内结构反应得到了有效控制，且半主动变刚度TLCD的减振性能要好于被动TLCD控制。

从图8还可看出，被动TLCD和SAVD-TLCD对结构的减振频带很窄，只有当ωp/ωs的值在1到1.2范围之内时，被动TLCD和SAVD-TLCD才能减小结构的反应，ωp/ωs的值在这个范围之外则没有减振效果。但是对于 SAVS-TLCD，在ωp/ωs的值为 0.8 到 1.2 范围之内，都能减小结构的反应。这表明SAVS-TLCD在振动的过程中，通过适时调整自身的频率，对外部激励具有一定的自适应特性，比被动TLCD和SAVD-TLCD具备更宽的减振频带。

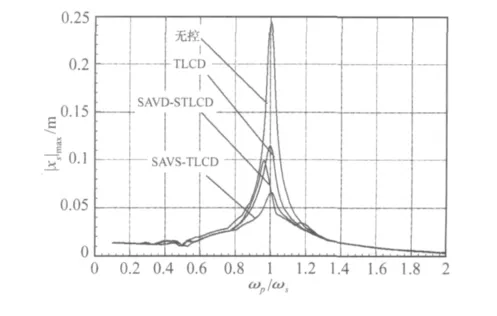
图8 结构最大反应随频率比ωp/ωs的变化曲线Fig.8 The curve of the maximum response of the structure with frequency ratio

表2 控制方案比较 （ωs=0.85）Tab.2 The comparison of control scheme（ωs=0.85）

当TLCD与结构的频率调谐至一致时，能对结构起到较好的减振效果。但是，由于测量、计算和制作的误差，以及结构使用期间活荷载的变化，使得TLCD的频率和结构的实际频率之间存在一定的不确定性。下面考虑这种误差对减振效果的影响。将结构的频率降低15%，即ωs=0.85，TLCD 频率依然为ωT=1 rad/s。分别考虑被动TLCD控制、SAVD-TLCD和SAVS-TLCD控制，外部荷载为谐波激励，计算结果如表2所示。由表中的数据可看出，由于结构的频率和TLCD的频率存在较大的误差，被动TLCD和SAVD-TLCD对结构的减振效果均下降很多，然而SAVS-TLCD仍能保持较好的减振效果，位移的减振率为69.5%，加速度减振率为69.89%。ωs=0.85时的位移和加速度时程曲线如图9和图10所示。

图9 位移时程曲线（ωs=0.85）Fig.9 The time history of displacement（ωs=0.85）

图10 加速度时程曲线（ωs=0.85）Fig.10 Time history of acceleration（ωs=0.85）

3 多自由度数值算例

为进一步验证半主动变刚度TLCD的减振作用，下面继续分析半主动变刚度TLCD对多层结构的减振性能。在一个n层的结构顶部，设置一个半主动变刚度TLCD减振装置后，体系的运动方程可表示为：

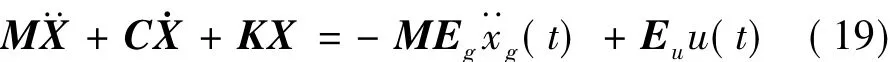
其中：X=［x1，x2，…，xn，xT］T，式中xi（i=1，…，n）表示结构第i层相对于地面的位移；Eg=［1 1 … 1 0］T表示地震力对控制体系的影响矩阵；Eu=［0 0 … 0 1］T表示半主动控制力的作用位置矩阵。M、C和K分别表示控制体系的质量、阻尼和刚度矩阵，具体表达式为：

u（t）为半主动变刚度TLCD的控制力，根据OTE控制策略，可表示为：

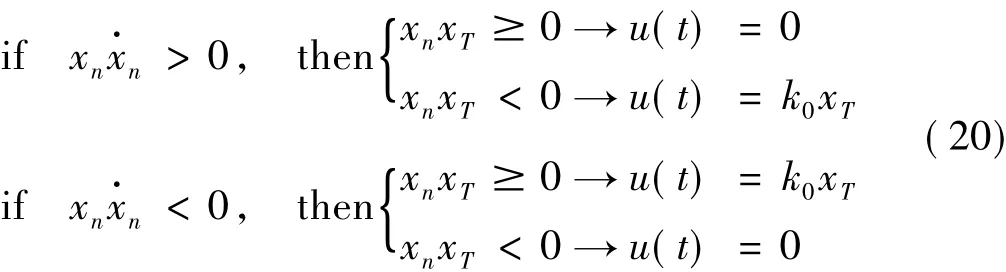
取一个五层结构的算例进行分析。这个算例来自于 Soong的专著［17］。结构的层间质量为每层131 338.6t，结构的刚度矩阵如式（21）所示。各阶振型的阻尼比假定为3%。结构的自振频率分别为0.24 Hz，0.35 Hz，0.42 Hz，0.49 Hz和 0.56Hz。

TLCD中的液体采用水，水的质量与结构的质量比为1%，TLCD装置的宽长比α=0.9。对于被动TLCD装置，将其频率调谐至结构振动的第一频率0.24 Hz；对于半主动变刚度TLCD减振装置，取可变刚度装置的弹簧刚度k0=0.8kTmax=9.322 8 ×106N/m，kT1=0.2kTmax=2.330 7 ×106N/m。

表3 结构各层的最大反应Tab.3 The maximum response of each story

图11给出了在谐波激励下，结构在未控、被动TLCD控制、半主动变刚度TLCD控制条件下顶层的位移时程曲线，图12给出结构在未控、被动控制和半主动变刚度控制时结构顶层的加速度时程曲线。由图中的曲线可看出，采用SAVS-TLCD控制方案后，结构顶层的位移和加速度反应都得到有效控制，且半主动控制的效果要好于被动控制的效果。

图11 结构顶层位移时程曲线Fig.11 The time history of displacement of top story

图12 结构顶层加速度时程曲线Fig.12 The time history of acceleration of the top story

现在考察地震作用下，半主动变刚度TLCD对五层结构的减振作用。结构参数和TLCD的参数与谐波激励情况相同，输入地震波为1940年El Centro地震记录，地震波的幅值调为0.1 g。分别计算结构无控、被动TLCD和半主动变刚度TLCD控制后结构的反应，结构各层的最大反应如表4所示。由表4可看出，在El Centro波作用下，采用半主动变刚度TLCD后，结构顶层的位移反应得到更好的控制。当采用被动TLCD控制时，减振率只有14.57%，而采用半主动变刚度TLCD控制后，位移的减振率提高到了24.38%。但是，对于下面几层结构，半主动变刚度TLCD的减振效果同被动TLCD的减振效果差不多。可见，半主动变刚度TLCD能有效减小结构顶部的位移反应，但是对下部结构的地震反应不是特别有效。

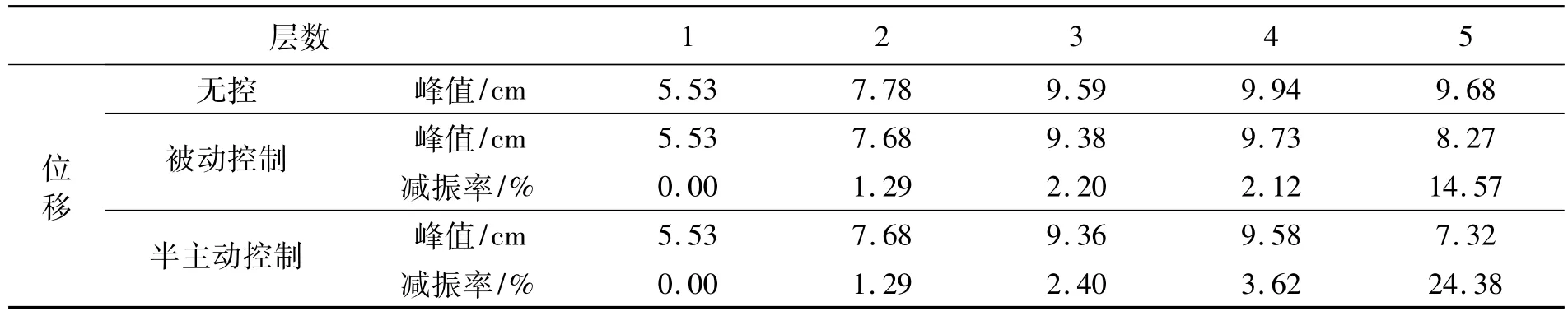
表4 结构各层最大反应Tab.4 The maximum response of each story

图13和图14分别给出了El Centro波作用下结构位移反应和加速度反应的时程曲线。由图中的曲线可看出，采用半主动变刚度TLCD控制后，能有效控制结构的反应。

图13 结构顶层的位移时程曲线（El Centro波）Fig.13 The time history of displacement of top story（El Centro wave）

图14 结构顶层的加速度时程曲线（El Centro波）Fig 14 The time history of acceleration of top story（El Centro wave）

4 结论

在可调频调液阻尼器的基础上，借鉴半主动变刚度装置的原理，提出了半变动变刚度TLCD（SAVSTLCD）减振控制装置。其基本原理是将可调频调液阻尼器的弹簧改装成半主动变刚度装置，按照一定的控制法则时，通过半主动变刚度装置中阀门的切换，来决定弹簧是否给系统提供刚度，从而改变TLCD中液体晃动的频率，以便更好地对结构振动实施有效控制。研究结果表明：

（1）当半变动变刚度TLCD的可变刚度取值越大时，结构的减振效果越好；

（2）半主动变刚度TLCD和半主动变阻尼TLCD都能改善被动TLCD的减振性能，但是半主动变刚度TLCD具有更宽的减振频带；

（3）TLCD的频率和结构振动的频率存在误差时，半主动变刚度TLCD仍能保持较好的减振效果。

［1］ Sakai F，Takaeda S，Tamaki T.Tuned liquid column damper-new type device for suppression of building vibrations［A］.Proceedings of the International Conference on Highrise Buildings［C］//Nanjing China，1989：926-931.

［2］Samali B，Templeton D，Kwok K S C.The effectiveness of multiple tuned liquid column dampers in controlling vibration of tall buildings subject to earthquake excitation［A］.Proceedings of 2nd International Conference on Motion and vibration Control［C］//Yokohama，1994：120-125.

［3］Gao H，Kwok K S C，Samali B.Characteristics of multiple tuned liquid columnsdampersin suppressing structural vibration［J］.Engineering Structures，1999，21（4）：316-331.

［4］李宏男，李忠献，祁 皑，等.结构振动与控制［M］.北京：中国建筑工业出版社，2005.

［15］霍林生，李宏男.环形调液阻尼器（CTLCD）对结构平移-扭转耦联振动控制的参数研究［J］.工程力学，2005，22（2）：124-131.

［6］李宏男，霍林生.调液阻尼器对结构扭转耦联振动控制的优化设计［J］.计算力学学报，2005，22（2）：129-134.

［7］Haroun M A，Pires J A.Active orifice control in hybrid liquid column dampers［A］.Proceedings of the First World Conference on Wind Engineering［C］//Los Angeles，USA，1994：69-78.

［8］ Abe M，Kimura S，Fujino Y.Control laws for semi-active tuned liquid column damper with variable orifice openings［A］. Proceedingsof2nd InternationalWorkshop on Structural Control［C］//Hong Kong，1996.

［9］Yalla S K，Kareem A.Semiactive tuned liquid column dampers：experimental study［J］.Journal of Structural Engineering，2003，129（7）：960-971.

［10］李宏男，阎 石，林 皋.建筑结构利用TLCD减振的神经网络智能控制［J］.地震工程与工程振动，2000，20（3）：137-142.

［11］李宏男，霍林生，闫 石.神经网络半主动TLCD对偏心结构的减震控制［J］.地震工程与工程振动，2001，21（4）：135-141.

［12］李宏男，金 峤.基于Takagi-Sugeno模型的半主动TLCD对偏心结构的减震控制［J］.计算力学学报，2003，20（5）：523-529.

［13］杨润林，闫维明，周锡元，等.半主动U型液力阻尼器的结构振动控制［J］.应用力学学报，2003，20（4）：108-111.

［14］阎 石，李宏男，林 皋.可调频调液阻尼器振动控制参数研究［J］.地震工程与工程振动，1998，18（4）：96-102.

［15］ Kobori T，Takahashi M，Nasu T，et al.Seismic response controlled structure with active variable stiffness system［J］.Earthquake Engineering and Structural Dynamics，1993，22（11）：925-941.

［16］杨润林.结构模糊振动控制的研究［D］.北京：中国建筑科学研究院，2002.

［17］ Soong T T.Active structural control-theory and practice［M］.Longman，London＆ Wiley，New York，1991.