基于泊松过程的超高斯随机振动试验控制技术研究
陈家焱,陈章位,周建川,贺惠农
(1.浙江大学 流体传动及控制国家重点实验室,杭州 310027;2.杭州亿恒科技有限公司,杭州 310003;3.浙江大学 生物医学工程与仪器科学学院,杭州 310027)
振动环境试验是指在实验室内利用激振设备使试件经受预先规定的振动,并达到预期目的的过程[1-2]。在已公开的关于随机振动试验规范中规定振动控制系统产生的随机信号应服从高斯分布。实践表明有些产品虽然通过了传统的随机振动试验,但其潜在缺陷仍然较多,当其经受超高斯随机振动环境时容易发生失效,从而影响产品的性能。随着对产品可靠性水平要求的提高,传统振动试验模拟的高斯分布振动环境已不能满足在某些场合的要求,特别是用于产品的环境应力筛选和可靠性增长试验[3]。模拟给定功率谱的高斯随机振动环境在技术上已经容易实现,但对给定功率谱的超高斯随机振动环境模拟技术目前还不成熟,存在一些技术实现难题,也成为振动试验模拟技术的研究热点。
国内外对超高斯随机振动试验控制的研究始于二十世纪九十年代,Smallwood[4-5]利用零记忆非线性变换法(Zero Memory Nonlinearity,ZMNL)对高斯随机信号进行非线性变换以得到满足特定要求的超高斯随机信号。ZMNL法在不断逼近参考功率谱的过程中同时控制随机信号的幅值分布特性,ZMNL法虽然能够控制输出信号的超高斯特性,但其功率谱控制的动态范围不高,影响振动试验模拟精度。Steinwolf[6-7]利用多项式函数变换实现非高斯随机试验模拟,从他的论文中可看出,采用多项式函数变换法的功率谱控制的动态范围也不高,同时对边缘频率控制不是很好。国内对超高斯随机振动试验控制研究代表是国防科技大学的蒋瑜博士[8],他利用二次相位调制的方法实现对超高斯随机振动试验的控制,并定量分析了时域随机化对超高斯随机信号的影响。北京航天航空大学的范文涛[9]和于英扬[10]也对超高斯随机振动控制进行了相关研究。国内对非高斯随机振动试验控制的研究主要集中在理论方面,具有实用价值的工程化的超高斯随机振动控制技术研究尚存在一些问题亟待解决。本文在广泛查阅国内外相关研究的基础上,提出基于泊松过程的超高斯随机振动试验控制方法,并进行系统实现,以期为随机振动试验控制系统的研发提供技术支持。
1 超高斯随机振动试验控制原理
1.1 超高斯随机涵义
高斯信号是指信号幅值的概率密度服从正态分布的随机信号,与之相对的非高斯信号是指信号的概率密度分布不服从正态分布。非高斯信号可分为亚高斯信号和超高斯信号,利用随机过程的前四阶累积统计量来进行数学描述:一阶中心矩描述信号均值μ,二阶中心矩描述信号方差σ,三阶中心矩描述信号偏斜度S,四阶中心矩描述的是信号峭度K,偏斜度与峭度的数学表达为:
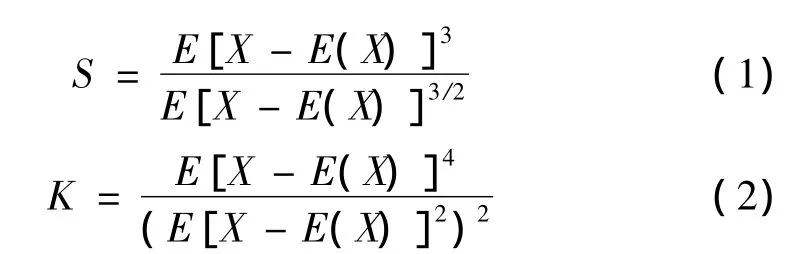
高斯随机信号的偏斜度恒为零,峭度值恒为3,它只需用均值和方差就可描述其特征。非高斯信号的偏斜度和峭度至少有一个条件与高斯信号不相符。
偏斜度是描述随机信号分布偏离对称分布的程度,峭度是描述随机信号幅值的波形特征的参数。以高斯信号的峭度值3为基准,峭度值小于3的非高斯信号为亚高斯信号,大于3的非高斯信号为超高斯信号。超高斯信号幅值概率密度的中心区域相对高斯信号更为狭窄,边缘地带的拖尾更长。蒋培[11]的研究表明在信号的均值和功率谱相同的情况下,超高斯信号对试件的累积疲劳损伤相对高斯和亚高斯信号的更大,能更充分地激发出试件的产品缺陷。本文主要以偏斜度为零的超高斯随机信号作为振动试验的研究对象,在振动台上实现超高斯随机振动试验的控制,进行相关的研究工作。
1.2 超高斯随机振动试验控制原理
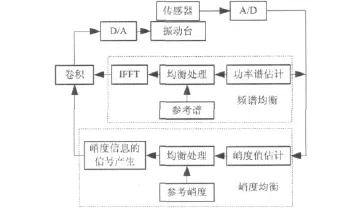
图1 超高斯随机振动试验控制流程Fig.1 Super-Gaussian random vibration test control process
超高斯随机振动试验控制相对于传统的随机振动试验除了要进行功率谱均衡,还须进行峭度控制,这在技术实现上相对复杂些。图1所示为本文采取的超高斯随机振动试验控制流程,利用传感器拾取振动响应信号,由A/D转换器转换成数字信号送入DSP,分别进行频谱均衡和峭度均衡,均衡完成后,两路信号进行卷积运算得到包含参考谱和参考峭度的驱动信号,然后将该驱动信号送入D/A转换器,实现对振动台的驱动。通过不断的反复迭代修正,使控制响应信号的功率谱和峭度与参考谱和参考峭度都达到误差允许的范围。频谱均衡方法包括自功率谱修正法、传递函数修正法和连续卷积法,详见文献[12]。对于峭度均衡过程,采用如图2所示的峭度控制算法流程。本研究采用两路并行控制策略实现对功率谱与峭度同时控制,完全不同于文献[8]的二次相位调制的控制方法,并行控制的两路信号相互独立,两者互不干涉,这在后续的仿真与实验中可进一步证明。

图2 峭度控制算法流程Fig.2 Kurtosis control algorithm process
2 基于泊松过程超高斯信号生成机理
2.1 滤波原理调制信号
从图1所示的超高斯随机振动试验控制流程图可知,系统控制的信号流分两路,一路是频谱均衡后输出信号,一路是峭度均衡后输出信号,最后两路信号通过卷积运算合成一路信号作为驱动信号激励振动台。为实现系统的有效控制,在控制环节进行了设计,把其中的频谱均衡输出信号设计成滤波器h(n),把峭度均衡输出信号设计成为输入信号A(n),驱动信号设计成线性时不变系统的输出x(n),如图3所示。根据图中所示的信号关系可调制出符合超高斯随机振动控制的驱动信号,实现对振动试验系统的控制。

图3 信号关系图Fig.3 Signal relationship chart
2.2 利用参考谱设计滤波器
利用振动试验给定的参考谱设计滤波器,脉冲响应函数h(n)是通过对给定的参考谱GR(f)进行傅里叶逆变换得到的。随机信号时域数据u(n)的幅值谱U(k)与功率谱Gu(k)之间存在关系:

其中N是随机信号时域数据长度,通常取2的整数次幂,Fs是采样频率,采样频率的选择应满足采样定理。根据上述条件,控制系统的频率分辨率Δf=Fs/N,采样间隔Δt=1/Fs,样本长度为T=NΔt,各离散频率点的频率值fk=k/T=kΔf。
根据式(3)可进一步推导出随机信号时域数据幅值谱的模与功率谱之间的关系:

利用参考谱设计滤波器时,根据式(4)得到信号的幅频特征:

进行傅里叶逆变换时必须要提供信号的相频特征,设计的滤波器信号相频特性须满足线性相位:
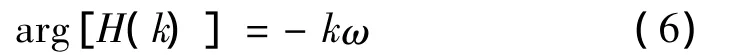
式中k是常数,此滤波器能保证信号无失真传输。出滤波的幅频特性与相频特性利用傅里叶逆变换得到时域信号:
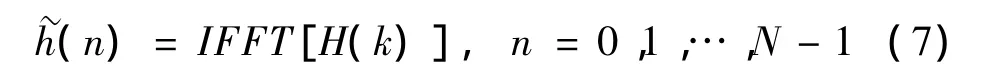
为了减小信号截断对脉冲响应函数信号造成的能量泄露,对得到的时域信号进行加窗并去除其均值:

推导至此,即完成了参考谱设计滤波器的过程。
2.3 基于泊松过程产生超高斯信号
通过峭度均衡得出控制系统驱动信号的峭度值,以该峭度值为依据产生出新信号,新信号包含期望的峭度控制信息同时又能够保证其为单位频谱满足控制系统要求。为产生满足上述要求的新信号,利用泊松过程[13]产生一些泊松点,在泊松点上加上信号值,同时赋予信号值一些统计特性,二者相互结合即可产生出符合要求的信号。在文献[14]中泊松过程产生的泊松点用参考谱设计的滤波器函数表示:
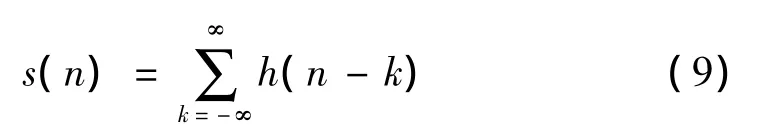
其中k是由指数分布的均值λ和采样间隔Δt所决定的独立时间参数,当λ的取值趋于无穷时指数分布即为高斯分布,本研究是利用λ取有限值来控制信号的峭度值,使信号输出具有超高斯特性。根据文献[14],得到泊松点的前四阶累积统计量:


由于两者之间相互独立,同时可得到x(n)的n阶累积统计量:

对于信号值A的随机过程,使其服从正态分布,A的四阶累积统计量可用其均值与方差描述。

由式(10)、(12)和(13)可推导出输入信号x(n)的四阶累积统计量:

根据式(1)和(2),且不考虑偏斜度,即S=0,对方程(14)求解得:


由此可得到基于泊松过程产生超高斯信号的参数,进而可产生出符合控制要求的超高斯信号。
3 数值模拟研究
为验证超高斯随机振动试验算法的合理性,利用Matlab软件进行相关的仿真研究。设置参考谱的频率范围20~450 Hz,采样频率取2 000 Hz,样本长度1 024,参考峭度值分布取10、15、20进行比较,控制系统的传递函数加入5%量级的噪声。仿真结果分析如下:表1中列出了参考峭度值在10、15和20时的相关参数的计算值。
限于篇幅这里只列出了参考峭度取15时控制算法的输出信号。图4所示控制仿真算法输出的超高斯时域随机信号的时间片段,图5所示控制算法对参考功率谱修正的输出情况,功率谱控制谱与参考谱之间的误差很小,完全满足工程上要求的±3 dB的报警限范围,表现出良好的功率谱控制性能。图6所示控制仿真输出响应信号的概率密度函数,并将其与高斯分布的概率密度函数进行对比,超高斯信号的概率密度图在均值附近的取值更加紧密,有较长的拖尾,有一部分信号值超出3σ的范围,有些信号值甚至达到6σ,满足控制系统的设计要求。

表1 控制参数计算值Tab.1 The calculated value of control parameters





4 实验研究
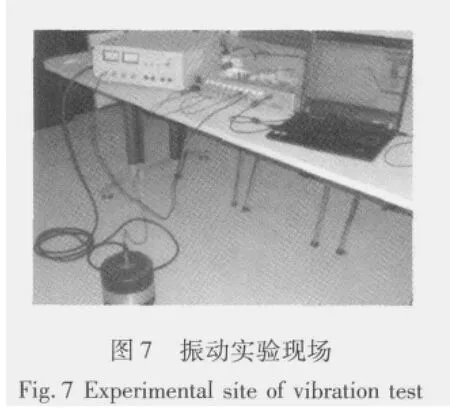
为进一步验证基于泊松过程的超高斯随机振动试验控制技术的正确性,对该控制策略进行了实验研究。实际振动试验系统都伴随着一定的非线性和随机噪声,这更能够证明该控制技术的实用性和有效性。通过构建完成的超高斯随机振动试验控制系统硬件和软件,在实验室内对试件进行了相关的振动实验,如图7所示是振动实验现场,利用该实验平台进行了实际连接激振器的超高斯随机振动实验。在实验中设置的频率范围5~2 000 Hz,幅值谱由上坡谱、下坡谱和恒定加速谱组成,设置的峭度值是10。图8所示是频率在5~2 000 Hz范围内功率谱控制结果,控制响应谱与参考谱之间非常紧密地贴合在一起,达到了很高的精度,完全满足工程试验中常用的±3 dB控制要求。图9所示是控制响应时域信号的峭度控制结果。图9中显示峭度控制在所有的时间历程里,峭度值波动都在目标峭度值附近,峭度达到了很高的控制精度,完全满足工程要求。
5 结论
在对国内外超高斯随机振动试验控制技术研究的基础上,提出了基于泊松过程的超高斯随机振动控制策略,结论如下:
(1)对超高斯随机振动试验控制原理进行了研究。给出了超高斯随机振动试验控制流程,对峭度控制算法进行了归纳,给出了峭度控制算法流程图。
(2)提出基于泊松过程的超高斯随机振动控制策略。采用数字滤波的方法调制超高斯随机信号,并以此信号作为控制系统的驱动信号,利用参考谱设计出符合控制要求的滤波器,通过泊松过程产生的泊松点,同时赋予泊松点的幅值满足正态分布,利用二者之间的卷积运算,实现了对超高斯随机振动试验控制系统的功率谱和峭度同时控制,且二者相互独立。
(3)仿真与实验结果表明,基于泊松过程的超高斯随机振动试验控制算法,其控制输出响应谱与参考谱的误差在很小的范围内,满足系统工程中常用的±3 dB控制要求,控制峭度值与参考峭度值之间的误差也在很小的范围,完全能够满足工程要求。
[1]陈章位,于慧君.振动控制技术现状与进展[J].振动与冲击,2009,28(3):73-77.
[2]陈章位,陈家焱,贺惠农.振动试验低频控制精度的研究[J].振动与冲击,2010,29(8):31-34.
[3]蒋 瑜,陈 循,陶俊勇.基于时域随机化的超高斯真随机驱动信号生成技术研究[J].振动工程学报,2005,18(4):491-494.
[4]Smallwood D O.Generating non-Gaussian vibration for testing purpose[J].Sound and Vibration,2005,39(10):18-23.
[5] Smallwood D O.Generation of partially coherent stationary time histories with non-Gaussian distribution[R].Sandia National Labs.,Albuquerque,NM(United States),1996:1-10.
[6]Steinwolf A.Closed-loop shaker simulation of non-Gaussian random vibration[J].Test Engineering and Management,2006,68(3):10-16.
[7]Steinwolf A.Random vibration testing beyond PSD limitation[J].Sound and Vibration,2006,40(9):12-21.
[8]蒋 瑜,陈 循,陶俊勇,等.超高斯伪随机振动激励信号的生成技术[J].振动工程学报,2005,18(2):179-183.
[9]范文涛,姜同敏,刁晓栩.基于电动振动台的非高斯随机振动控制技术的研究和实现[J].装备环境工程,2008(2):41-43.
[10] NU Y Y,Jiang T M.Generation of non-Gaussian random vibration excitation signal for reliability enhancement test[J].Chinese Journal of Aeronautics,2007,27(3):236-239.
[11]蒋 培,温熙森,陈 循,等.非高斯随机应力载荷频域疲劳寿命估计方法[J].机械工程学报,2006,42(2):51-56.
[12]王述成,陈章位.随机振动试验中时域随机化技术的研究[J].机械工程学报,2005,41(5):230-233.
[13]帕普里斯.概率、随机变量与随机过程(第4版)[M].西安:西安交通大学出版社,2004.
[14] Smallwood D O.Generation of time histories with a specified auto spectral density,skewness,and kurtosis[R].Sandia National Labs.,Albuquerque,NM(United States),1996:1-10.

