PFWD在粉土路基施工质量控制中的应用研究*

张孝彬，乐金朝

(郑州大学交通运输工程系，河南郑州450001)

回弹模量是对路基质量评价的一个重要指标。目前道路工程中检测路基回弹模量主要有两大类方法：静态检测方法，得到路基的静态回弹模量，与路基实际受力状态存在一定差异，主要有承载板法、贝克曼梁法、自动弯沉仪法等［1］;动态检测方法，得到路基的动态弹性模量，主要有落锤式弯沉仪(FWD)法和PFWD法［2］。承载板法是我国现行规范中路基回弹模量的标准试验方法，但是这种方法必须在已建好的路基上进行，且存在测试时间长的缺点。FWD虽然能够快速可靠地得到路基的动态弹性模量［3］，但是成本较高，并且受地形限制。PFWD是在FWD的基础上发展而来的一种新型简易快速检测设备，具有易携带、操作简便和处理数据快而精确的优点。

2 PFWD简介与测试原理

PFWD由加载系统、数据采集系统和数据传输系统组成，加载系统由落锤、滑杆、锁定杆和橡胶垫块等机械装置组成，数据采集系统由压力传感器、位移传感器和采集装置等组成，数据传输系统由计算机、有线数据传输装置、无线数据传输装置和数据处理软件等组成，如图1所示。

进行PFWD测试时，将一固定重的落锤提升至一个固定高度，然后释放，让落锤自由下落，冲击置放在路基表面的承载板，承载板与路基表面产生竖向位移。由此，压力传感器和位移传感器将荷载和位移的时程数据记录下来，并传输到计算机数据处理软件中，然后根据压力和位移的峰值来确定路基的动态弹性模量。

PFWD的基本原理是弹性半空间接触理论。假定在弹性半空间表面有一个半径为R的圆形压板。单位面积压力为根据弹性半空间理论［4］，圆板中心下(z轴)位移的表达式如下：

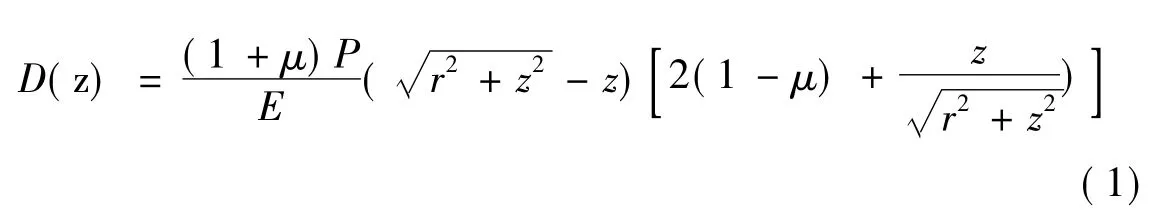
式中μ和E分别为泊松比和动态弹性模量。设z为0，圆板中心下位移D0和动态弹性模量E之间的关系公式如下：

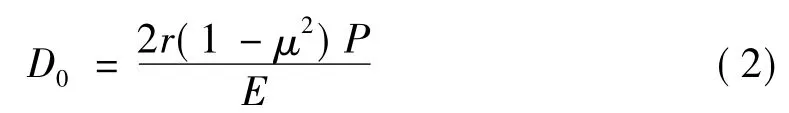
于是，以压力和位移峰值为基础，动态弹性模量的计算公式如下：

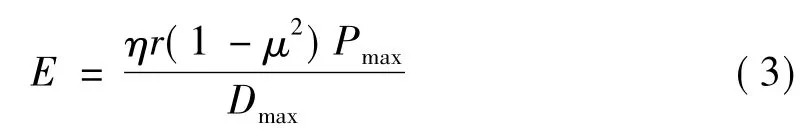
式中：E——PFWD的计算动态弹性模量(MPa);

η——材料参数值，取η=2;

r——压板的半径(mm);

μ——泊松比;

Pmax——最大压力(kPa);

Dmax——最大位移(m)。

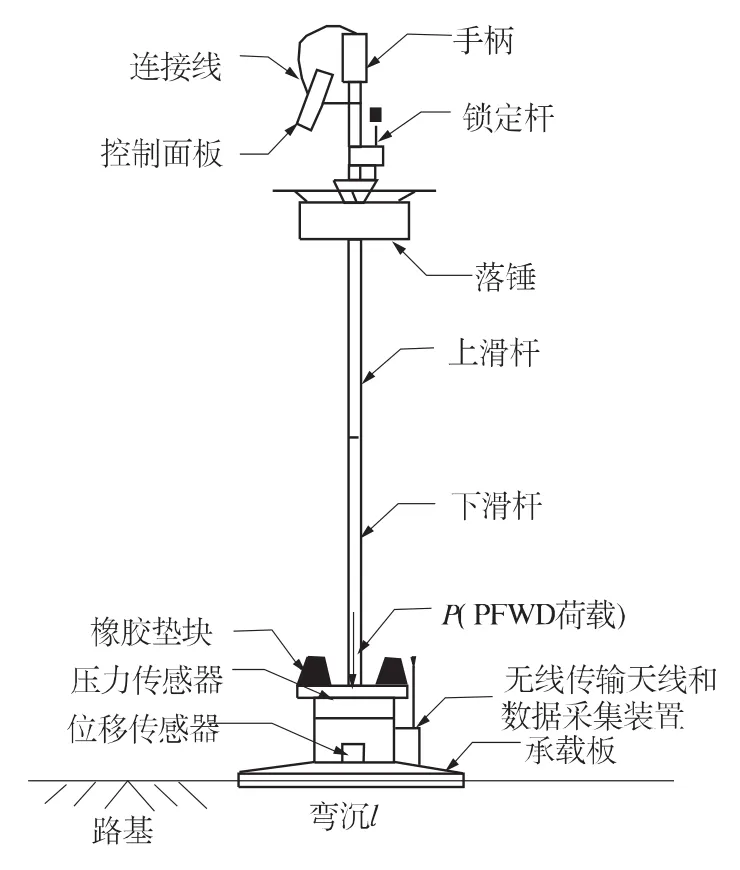
图1 PFWD构造与工作原理示意图

3 试验结果及分析

在郑州至民权高速公路路基施工现场选取桩号K35+100—K45+683之间的测点(从94区和93区两个不同的压实区选择)，分别对成型路段进行了承载板和PFWD法现场检测。由于篇幅有限，现将部分试验数据结果列出，见表1。

表1 PFWD和承载板的试验结果MPa

丁学峰［5］等依托某二级公路项目，对PFWD在路基施工质量控制中的应用进行了研究，基于现场试验得到的数据结果，采用5种模型模拟动态弹性模量和静态回弹模量之间的关系，具体为：直线模型、半对数模型、指数模型、抛物线模型、双对数模型。其研究结果表明，5个模型中双对数模型的相关性最好。本文根据试验数据结果，利用五种模型分别对93区和94区的PFWD动态弹性模量Ep和承载板静态回弹模量Eb进行模拟，结果见表2。

从表2中可以看出，对于93区和94区，各种模型的相关性都很好，相关系数约为0.9。若采用抛物线模型来拟合Eb和Ep之间的关系是不合理的，因为Eb和Ep的关系为单调关系，不存在峰值;若采用半对数关系进行拟合，则难以较好地体现正比特性;用直线关系来拟合，则存在没有任何物理意义的截距。基于现场的实验结果，经过比较分析，推荐以下的拟合计算公式：

对于93区：Eb=1.5231E0.8840P，相关系数为0.909;

对于94区：Eb=21.924e0.0162Ep，相关系数为0.926。

4 结语

(1)PFWD是基于FWD发展而来的一种无损检测设备，具有携带方便、操作简单、检测速度快、精度高等特点。

(2)PFWD测试时所施加的为动态荷载，能更好地模拟实际荷载情况。同时，根据PFWD实测的冲击荷载和路基表面竖向位移的峰值，按圆形垂直刚性分布荷载作用下的弹性半空间理论弯沉公式来计算路基模量。

(3)在粉土路基施工现场，分别从93区和94区两个不同的压实区选择测点，进行PFWD试验和承载板试验，对比PFWD和承载板检测结果，建立PFWD测得的动态弹性模量和承载板测得的静态回弹模量之间的相关关系方程，结果表明，针对粉土路基，93区可以采用双对数模型，94区可以采用指数模型，采用的各模型相关性良好，所以，利用具有操作简便、检测高效和无损检测优势的PFWD进行粉土路基模量的快速检测是合理可行的。

［1］JTGE60-2008.公路路基路面现场测试规程［S］.

［2］徐平，王复明，陈忠平.PFWD在路基强度评价中的应用［J］.路基工程，2008(5)：52-54.

［3］姬亦工，王复明，郭忠印.基于落锤式弯沉仪(FWD)动态数据的路面模量反演方法［J］.土木工程学报，2002，35(3)：31-36.

［4］李同林.应用弹塑性力学［M］.北京：中国地质大学出版社，2002.

［5］丁学峰，邓鲲，李跃军.PFWD在路基施工质量控制中的应用研究［J］.湖南交通科技，2009，35(4)：29-32.