一个多翼混沌系统的分析和同步*
胥红星
(郑州航空工业管理学院,河南郑州450046)
混沌是一种在确定性系统中所出现的类似随机而无规则运动的动力学行为,是非线性动力学中所特有的一种运动形式.近年来,人们对混沌现象的自然规律及其在自然科学和社会科学中的表现形式有了广泛而深刻的认识,它广泛存在于自然界中,在诸如物理、化学、生物学、地质学、技术科学以及社会科学中有着广泛的用途.自20世纪60年代Lorenz[1]发现了第一个混沌吸引子以来,很多混沌系统被发现,如Chen系统[2]、Rossler系统[3]、Chua系统[4]等,其复杂的动力学行为已经得到广泛的研究.
目前,能产生混沌吸引子的方法已经很多,如状态反馈[5]等,在吸引子的拓扑结构方面,由于传统的Lorenz系统族只能产生两个翼,Chua产生的吸引子只有两个涡卷,结构均较简单.为了研究和考察混沌系统更丰富的动力学行为,在Lorenz系统族的基础上,对微分方程做些调整,使得能够产生多翼混沌吸引子的混沌系统相继被提出,但其方程结构较为复杂,文献提出一个结构简单且随着单参数变化而能够产生一翼、二翼、三翼及四翼的四维混沌系统,使得混沌系统的理论体系进一步完善.
混沌现象最初被认为是不能被控制的,但1990年Ott、Grebogi和Yorke提出了OGY混沌控制方法,同时Carroll和Pecora提出混沌同步的思想和方案,使混沌控制与同步的研究工作取得了进展.学者们先后提出了诸多混沌控制与同步的方法,如线性耦合方法[6]、自适应方法[7]等.本文将进一步分析该系统的特性以及借助于线性反馈方法研究该系统的同步性,并用数值仿真验证了控制方法的有效性和理论推导的正确性.
1 系统的描述
Yu[8]等提出了一个新的四维二次系统,这个光滑的四维系统能产生复杂的动力学行为,系统方程为:其中,a、b、c、d、e为系统参数,x、y、z、u为状态变量.当b-a-c-e<0系统是耗散的.当a=10、b=12、d=2、e=4时,随着参数c的变化,该系统分别能够产生一翼、二翼、三翼及四翼的混沌吸引子,分别见图1、图2、图3、图4.

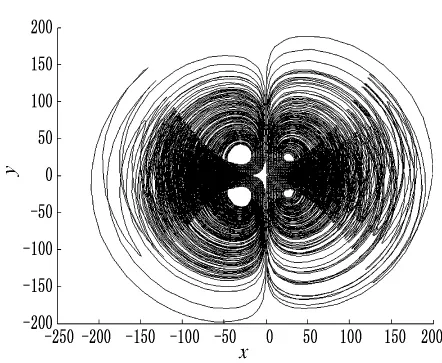
图1 当a=10、b=12、c=50、d=2、e=4时,系统(1)在x-y面的四翼混沌吸引子

图3 当a=10、b=12、c=62、d=2、e=4时,系统(1)在x-y面的二翼混沌吸引子

图2 当a=10、b=12、c=60、d=2、e=4时,系统(1)在x-y面的三翼混沌吸引子
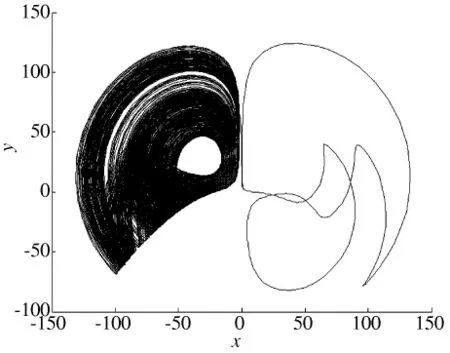
图4 当a=10、b=12、c=53、d=2、e=4时,系统(1)在x-y面的二翼混沌吸引子
假设系统(1)为驱动系统,相应的响应系统为:
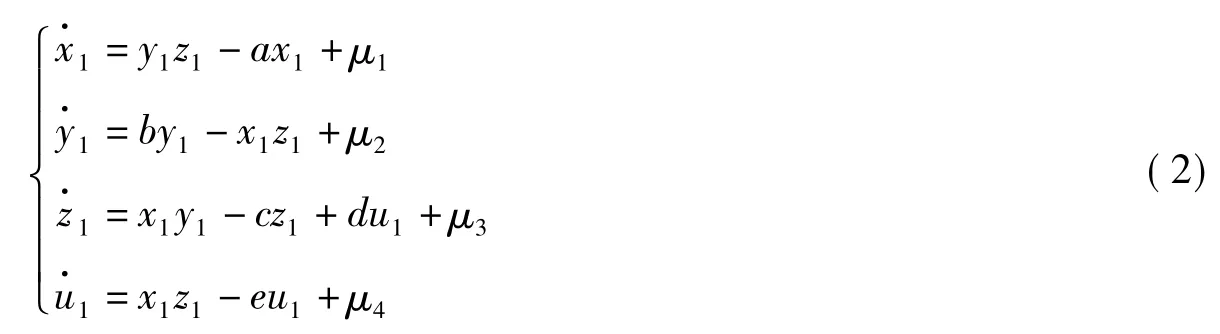
其中,ui(i=1,2,3,4)为要设计的控制器.要解决的问题是如何仅用系统(1)的某一个状态变量作为驱动变量实现系统(2)与系统(1)的同步,或如何设计控制器ui(i=1,2,3,4)使系统(2)与系统(1)同步.但ui(i=1,2,3,4)中只含有系统(1)的某一个状态变量.
2 系统的线性反馈同步
取μ1=0,μ2=-k2e2,μ3=-k3e3,μ4=-k4e4,ki>0(i=2,3,4)为反馈系数.
定义系统(1)和系统(2)的误差状态变量为:
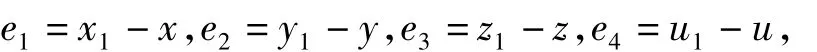
则误差系统为:

证明对误差系统(3)构造如下径向无界正定的Lyapunov函数
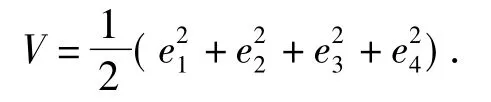
对V沿着系统(3)的轨道求导得:
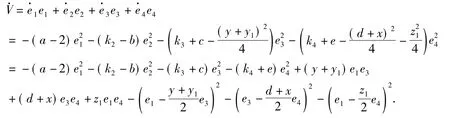
由Lyapunov第二方法知:误差系统(3)在零点是渐进稳定的,即系统(1)和系统(2)是全局同步的.
3 系统的非线性反馈同步
证明将控制器代入式(2)并减去式(1)得到如下误差系统:
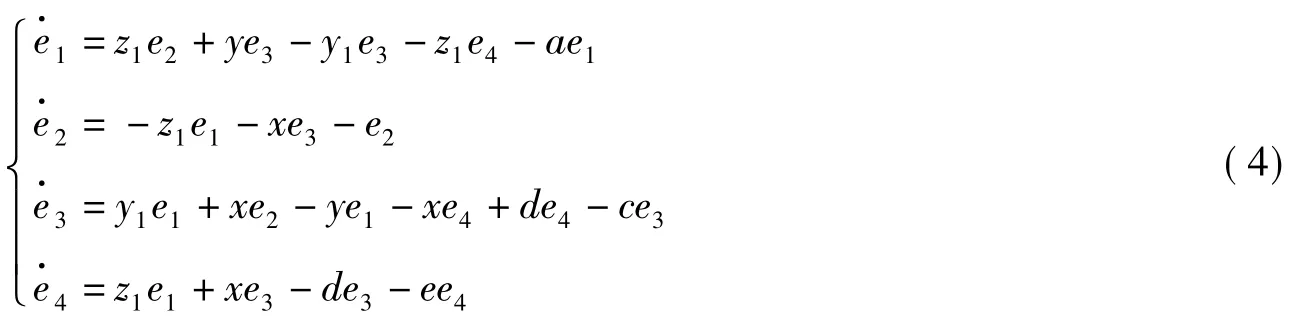
对误差系统(4)构造如下径向无界正定的Lyapunov函数:

对V沿着系统(4)的轨道求导得:

由Lyapunov第二方法知:误差系统(4)在零点是渐进稳定的,即系统(1)和系统(2)是全局同步的.
4 数值仿真
为了验证理论结果,用Matlab程序进行数值仿真.在仿真过程中驱动系统和响应系统初值为(1,1,1,1)和(-1,4,0,2.5),选取参数a=10、b=12、c=50、d=2、e=4,根据定理1可选择k2=13、k3=300、k4=320,则驱动系统(1)和响应系统(2)是全局同步的.如图5所示.
图6表示在定理2中的非线性控制器的作用下响应系统(1)与驱动系统(2)的同步误差随时间的演化.
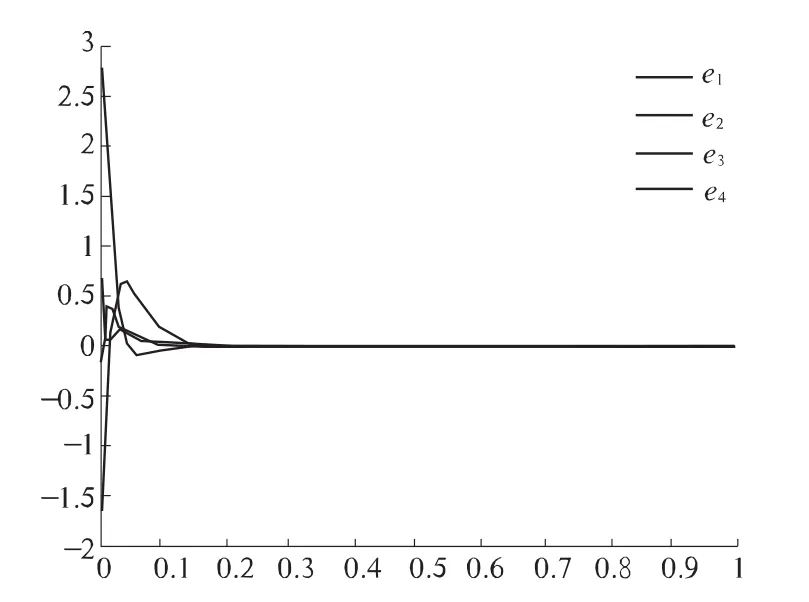
图5 线性反馈控制下的同步误差
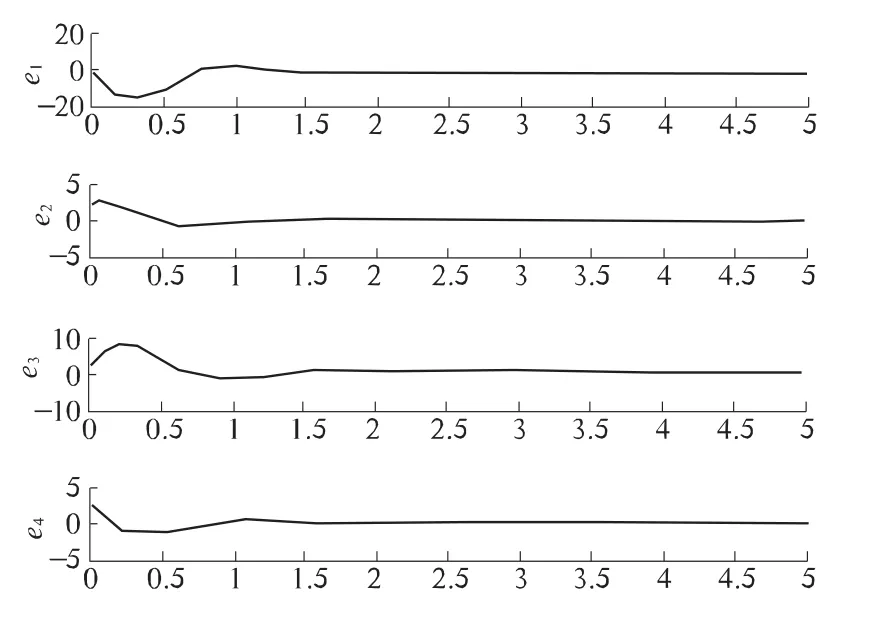
图6 非线性反馈控制下的同步误差
5 结论
讨论了一个四维分别产生一翼、二翼、三翼及四翼混沌吸引子的形成机制,借助于线性和非线性控制器实现系统的完全同步,最后给出数值仿真验证了理论的有效性.
[1] LORENZ E N.Deterministic non-periods flows[J].J Atmos Sci,1963,20(2):130-141.
[2] ROSSER O E.An equation for continuous chaos[J].Phys Lett A,1976,57(5):397-398.
[3] CHEN G,UETA G T.Yet another chaotic attractor[J].Int J Bifurcat Chaos,1999,9(7):1465-1466.
[4] MATSUMOTO T.A chaotic attractor from Chua's circuit[J].IEEE Trans Circ and Syst 1984,31(12):1055-1058.
[5] 彭建奎,俞建宁,王振乾.一个新混沌系统的混沌分析及电路仿真[J].河北师范大学学报:自然科学版,2010,34(6):656-663.
[6] SHY Y L,Zhang Y.Globally attractive set and feedback synchronization of the BLDCM system[J].Journal of East China Normal University,2010(1):62-68.
[7] GAN Q T,HU R X.Adaptive synchronization for stochastic competitive neural networks with mixed time-varying delays[J].Commun Nonlinear Sci Numer Simul,2012,17(9):3708-3718.
[8] 胡国四.一个具有四翼吸引子的超混沌系统[J].物理学报,2009,58(6):3735-3740.

