基于Wrapper的信用风险预测模型研究与应用
张凯
(河南城建学院,河南平顶山467036)
信用风险是指交易对象无力履约而给交易另一方带来损失的风险,也即债务人未能如期偿还其债务造成违约而给经济主体经营带来的风险[1]。通过对传统的单一神经网络的预测模型的使用效率和准确率均较低等问题进行分析后,发现此类模型主要存在以下问题:(1)对指标的选择缺乏科学依据,指标之间存在很强的共线性;(2)模型的条件太严格,如要求指标数据是正态分布,各组的协方差是相同的,造成模型的适用范围不广泛;(3)入选指标过多,学习时间较长。这些问题都与选择合适的指标有很大关系。
本文通过遗传算法搜索最优特征子集,在使用神经网络模型进行预测之前,使用基于Wrapper的方法对入选指标进行特征选择,达到提高学习的预测精度,即首先选择最优特征子集,然后通过训练样本对未知样本进行预测的方法建立一种改进的神经网络预测模型,以解决信用风险度量的准确率较低的问题。
1 Wrapper预测模型原理
1.1 Wrapper特征选择
特征选择是根据某种目的所确定的标准,从一个数据集的所有特征中选择出一个较小的特征子集,该特征子集可以更好地满足所需目的。通过选择原特征集合的一个子集,提高用于分类和回归模型的预测正确率,或者在保证一定预测正确率的条件下降低模型结构的复杂性[2]。在一个机器学习算法通过训练样本对未知样本进行预测之前,必须决定哪些特征应该采用,哪些特征应该忽略。
特征选择和后续学习算法的结合方式这里采用Wrapper方法。Wrapper方法的主要思想是:和学习算法无关的过滤式特征评价会和后续的分类算法产生较大的偏差,而学习算法基于所选特征子集的性能可以作为更好的特征评价标准。因此在Wrapper特征选择中将学习算法的性能作为特征选择的评估标准。
1.2 人工神经网络
在模型中采用的神经网络是基于BP算法[3]的前向反馈MLP网络。由于一个三层的BP神经网络可以任意精度地逼近任意映射关系,而且与一个隐含层相比,用两个隐含层的神经网络训练无助于提高预测的准确率,因此本文采用三层前向型神经网络的拓扑结构。它是具有明显层次结构的网络模型。网络由输入层、输出层和若干隐层组成,网络之间通过神经元(节点)顺序单向联接。每一层神经元只接受前一层神经元的输入,并在节点上进行复合(线性叠加)和畸变(非线性映射)。
通过复合反映不同神经元之间的耦合作用和耦合强度(由相对权值表征),通过畸变改变输入信息的结构和性态。其特性由简单的数学函数所描述,神经元i接收其它神经元传递来的输入信息,根据和函数neti进行加权平均,然后根据传递函数fi产生输出信息,输出信息又按照网络的拓扑结构传递到下一个神经元。前向网络采用下面的传递函数:
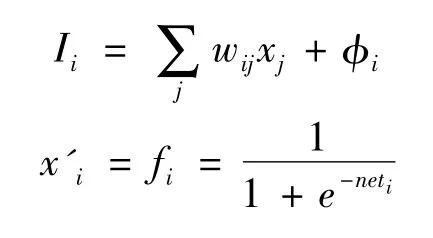
式中:Ii为神经元i的层输入;x'i为神经元的输出;wij为神经元i、j之间的连接权;φi为神经元i的偏置。
2 预测模型实例
2.1 实验样本的选择
在遵循随机原则的基础上,样本取自沪深股市1998—2004年内的制造业上市公司。样本集选择被特别处理[4](ST)的上市公司39家,另选取与ST公司同行业、同规模、同样年份、经营正常的39家公司作为配对样本,在这78家公司中再重新选择53个样本作为训练集,另外25个样本为预测集。
本文中的出现信用风险的年份是指公司被ST的当年往前追溯所得的会计年度数,把公司被ST的当年定义为财务困境前的第T年。例如,出现信用风险前1年,是指实施ST当年的前1年,用T-1表示。
2.2 变量选择
我国上市公司被特别处理的本质原因不尽相同,很难用简单的几个财务指标变量充分描述[5]。在我国,上市公司出现财务风险的成因是多方面的、综合的,因此为了避免人为因素的干扰,尝试从反映公司各个方面的财务比率入手,尽可能多的选择财务指标变量,然后在建立模型时选择最优的一组变量子集。本文选择了32个常见的财务比率,具体见表1。

表1 入选财务比率
2.3 数据预处理
由于进行特征选择之前要先对数据进行单位化处理,设特征对应的集合为{T1,T2,T3,…,T31,T32},对于特征Ti对应的值xi1,xi2,xi3,…,xi77,xi78,在分析了多个指标之后,证实多数指标不服从正态分布。为防止财物指标所表示的信息在单位化后出现失真,甚至丢失的情况,在对数据进行认真分析后,选择了下式对数据进行单位化:

式中max3、min3分别为xi1,xi2,xi3,…,xi77,xi78中的第三大值和第三小值。对于极端值xij,如果xij>max3,则令=1,反之,如果xij<min3,则令=0。
3 基于Wrapper的神经网络信用风险预警系统模型设计
3.1 建立预测系统模型
本文建立模型时采用遗传算法进行特征选择,遗传算法中的适应度值采用神经网络的测试误差,该误差通过训练神经网络得到,最后用经过选择后的特征对神经网络进行训练和预测。
具体描述如下:
(1)对数据进行单位化。
(2)初始化染色体长度(lchrom)、最大世代数(maxgen)、交叉概率(pcorss),变异概率(pmutation),神经网络的学习率(Alpha)、神经网络的误差增量(Eta)、调用神经网络计算适应度(fitness)。
(3)开始遗传算法操作,随机生成基因个体(popsize)。
(4)依据轮盘赌方式进行选择。
(5)随机生成交叉位置(xsite)进行交叉操作。
(6)进行变异操作。
(7)计算新生成的基因个体的适应度,判断是否达到终止条件,如未达到则转(3),如达到终止条件则进行步骤(8)。
(8)依据最优基因个体调整入选变量的个数和隐层神经元的数量,用筛选后的数据对神经网络进行训练、测试,输入预测数据进行预测。
3.2 BP神经网络的具体参数设置
BP神经网络的设计包括输入层、隐层、输出层、传递函数、训练函数等网络结构的设置,具体设置如下:
(1)输入层:输入层神经元个数由输入特征决定。未进行特征选择前使用确定的神经元个数32,进行特征选择后神经元的个数依据最优特征子集的个数而定。
(2)输出层:输出层神经元的个数由输出类别决定。具体到本文,网络的输出层定义为一个节点,即上市公司的实际财务状况。在训练样本集中,第i样本的输出量为Y(当为ST公司时,Y=1;当为非ST公司时,Y=0)。
(3)隐层:对未使用特征选择的神经网络进行训练和预测,比较3年内的误判率,依据误判率来确定隐层神经元数。
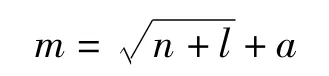
式中:m为隐层神经元数;n为输入神经元数;l为输出神经元数;a为1~12之间的常数。
a分别取2-12之间的值,出现信用风险前一年的误判率,发现a=2时误判率为44%,随着a的增大,误判率逐渐减小,当a=8或a=10时,误判率降到最小,而当a继续增大后,误判率也增大到了48%。因此,使用神经网络时,a均取8。
(4)传递函数:传递函数的好坏对一个神经网络的训练效率至关重要,这里采用Sigmoid[6]型函数。
(5)训练函数:选取了基于动量因子算法规则的BP算法。
3.3 遗传算法的具体参数设置
在确定了神经网络的相关参数后,需要确定遗传算法中的一些参数,依据遗传算法的基本步骤,设置如下:
(1)确定编码方式和定义适应度函数f(x):采用0、1二进制编码,将需要进行筛选的特征向量表示成二进制位串。其中0表示不选择该变量,1表示选择该变量。适应度函数f(x)使用由神经网络计算出的最小累计误差的倒数。
(2)产生初始群体:初始群体是遗传算法的一个重要参数,参数设置直接影响算法的复杂度。基于这样的考虑,经过多次实验最终确定初始群体为20。同时为了保证算法的并行性,在程序设计时,设种群参数为5。种群的设定可以使算法避免陷入局部无穷小。
(3)停机条件的判断:若群体中存在最优个体,或已满足预先设定的停机条件——达到最大基因代数,则输出最优解后停机。
(4)选择算子、交叉算子、变异算子的设定:选择算子主要采用轮盘赌方式;使用单点交叉,交叉位置通过计算机随机生成,交叉概率为0.8;变异算子设定为0.005,变异位置由计算机随机给出。
4 预测模型实验与结果分析
为了验证新模型的有效性和可行性。文中首先使用未进行特征选择的神经网络进行训练和预测,然后使用特征选择寻找最优特征子集后,再使用神经网络输入最优特征子集对应数据进行训练和预测,并分析不同网络下三年内的误判率。
4.1 实现预测模型程序
程序采用C语言进行编程。具体的程序流程如图1所示。
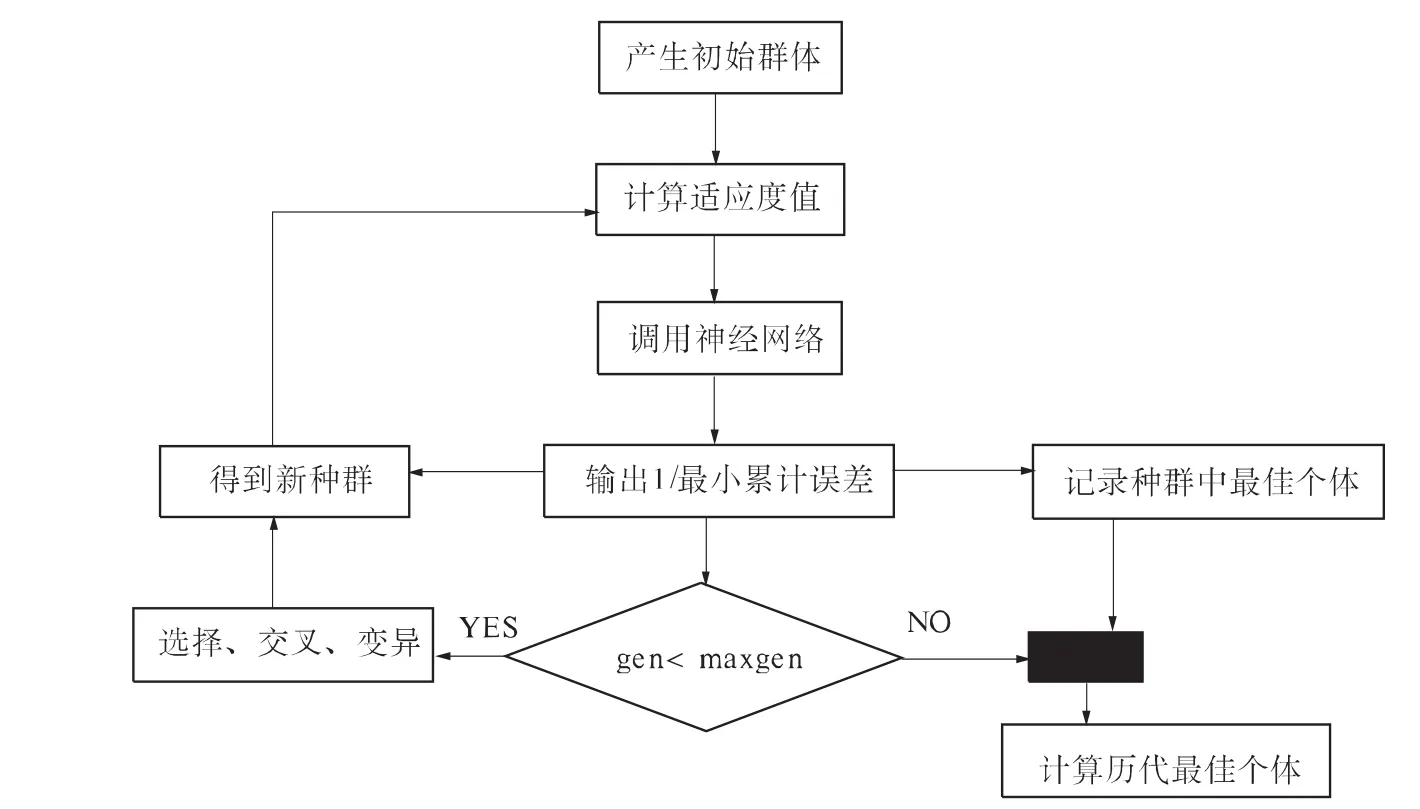
图1 预测模型程序流程
4.2 实验结果
为了得到使用Wrapper方法后模型的误判率,先使用当年样本的训练数据进行训练,然后使用当年样本的预测数据进行预测。表2列出了使用遗传算法后形成的基因串的情况以及基因对应的适应度值。表3列出了使用最优特征子集进行预测的结果。

表2 特征选择后的基因串与适应度值
4.3 结果分析
为了评价优化后的预测模型的误判率,使用单一BP神经网络对上市公司三年后出现信用风险的情况进行了训练和预测。预测结果如表4所示。
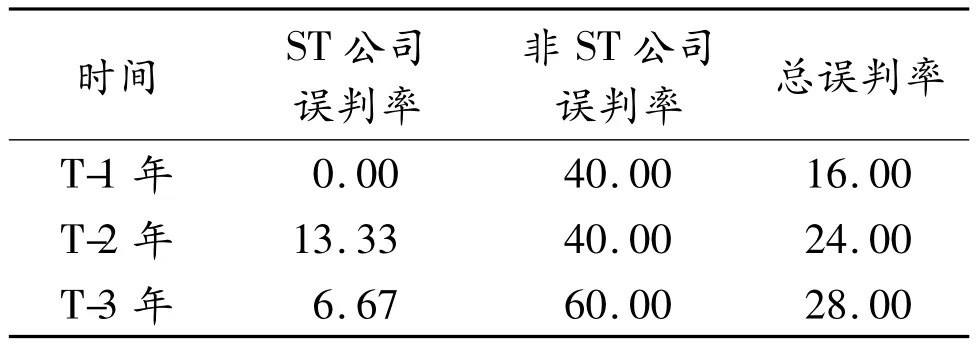
表3 特征选择后的误判率%
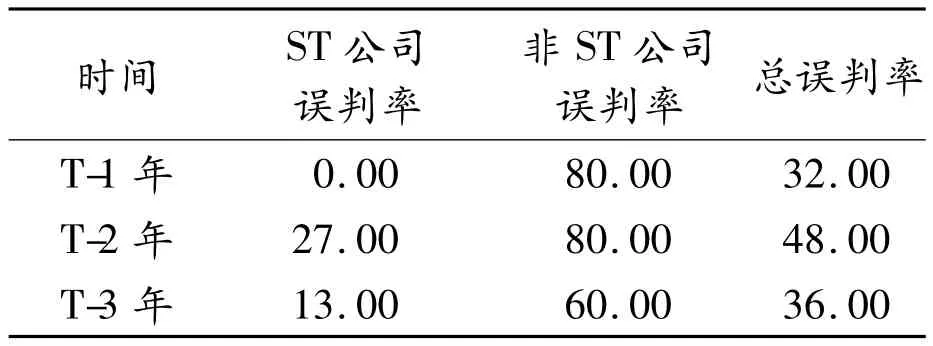
表4 单一BP神经网络模型的误判率%
经分析后发现神经网络对于非ST公司的误判率非常高,T-1年、T-2年的误判率都达到了80%(在预测样本中共有10家非ST公司,误判率80%意味着神经网络仅判断正确了两家公司,而对其余8家公司都做出了错误判断),前3年的误判率也有60%之多。
同单一BP神经网络的预测系统相比,本文的预测系统后3年的误判率均有不同程度的降低。其中T-2年的误判率降低的最多,总误判率从48%降到了24%。
5 结束语
针对单一BP神经网络预测模型由于财务指标选择不当导致误判率较高的问题,提出了一个基于Wrapper方法的神经网络信用风险预测模型。该模型首先使用基于Wrapper方法从特征集中搜索最优特征子集,然后使用神经网络对最优特征子集所对应的数据进行训练和预测。实验结果表明,在使用特征选择后,神经网络的输出速度明显加快,且输出准确率也有较大的提高。
[1] 赵晓菊,柳永明.金融机构信用管理[M].北京:中国方正出版社,2004.
[2] Kohavi R,John G H.Wrappers for feature subset selection[J].Artificial Intelligence,1997,97(1-2):273-324.
[3] 杨梅,卿晓霞,王波.基于改进遗传算法的神经网络优化方法[J].计算机仿真,2009(5):198-201.
[4] 岑涌,钟萍,罗林凯.基于GA-SVM的企业财务困境预测[J].计算机工程,2008,34(7):223-225.
[5] 张丽新,王家钦,赵雁南,等.机器学习中的特征选择[J].计算机科学,2004(11):180-184.
[6] 陆锁军,苗清影,郭钊侠.基于预测的遗传算法[J].计算机仿真,2009(3):183-186.

