基于PSO-SVM的交通流量短时预测
王树洋,黄天民,方 新
(西南交通大学数学学院,四川成都 610031)
基于PSO-SVM的交通流量短时预测
王树洋,黄天民,方 新
(西南交通大学数学学院,四川成都 610031)
参数选择问题影响了支持向量机预测模型在交通流量中的预测性能。为了解决支持向量机预测模型的参数选择问题,引入了粒子群优化算法机制,通过粒子群优化选择支持向量机预测模型的学习训练参数,得到较优的PSO-SVM预测模型。通过实例仿真实验,将PSO-SVM预测模型与神经网络预测模型进行了比较,显示了其优越性。
支持向量机;粒子群优化算法;神经网络;预测;交通流量
交通流量预测作为智能交通系统(ITS)的基础,其实时准确的短时预测是实现科学规范的交通规划、交通诱导和交通控制的关键技术。真实的交通流量具有随机性、非线性、复杂性、不确定性,无法建立精确的数学模型,因而采用人工智能方法对交通流量预测越来越受重视[1]。在交通流量预测中,神经网络凭借其逼近任意非线性函数的能力和所具有的容错、自学习等优点,已被国内外学者广泛的采用[2]。但是,基于经验风险最小化原则的神经网络,结构选择缺乏理论指导,容易陷入局部极值点,经验风险不能达到最小,所以神经网络的推广能力不能得到很好的控制。
支持向量机(Support Vector Machine,SVM)是近年来出现的机器学习方法,在解决小样本、非线性和多变量的分类和回归问题中表现出优势。SVM避免了神经网络等方法存在的陷入局部最优解的问题,也避免了神经网络在学习小样本问题时出现的“过学习”问题,因此 SVM具有较好的泛化能力[2-5]。SVM的参数选择问题一直是一个未完全解决的研究领域[3]。然而训练学习参数的选择对SVM模型的预测性能有很大的影响,笔者将PSO与SVM相结合,用PSO优化选择SVM模型的训练学习参数,得到较优的PSO-SVM预测模型,并用于城市道路交通流量的预测。
1 SVM原理
支持向量机是由Vapink教授提出的一种统计学习方法,近年来在其理论研究和算法实现方面都取得了突破性的进展,成为了克服维数灾难、过学习及局部最优等传统困难的有效手段。该方法具有学习速度快,全局最优和泛化能力强等优点,其学习结果明显好于其它传统的回归预测方法,并在模式识别、系统建模、信号处理、最优控制等领域得到了广泛的应用[3]。
支持向量机的方法应用于回归问题,得到支持向量回归机(Support Vector Regression,SVR)。支持向量回归机基本的思想可解释为:给定样本集(x1,y1),…,(xl,yl),其中:xi是第i个n维的输入向量;yi是对应的第i个输出量;l是训练样本数目,寻找输入量与输出量之间的映射关系f。首先通过非线性映射Φ,将样本集中的n维输入向量映射到m维的特征空间F内,然后在m维特征空间F内构造优化的线性回归函数,即:
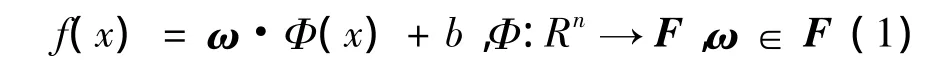
式中:ω为权重向量;b为偏置项。可以通过求解最优化问题得到系数ω和b。
为了提高预测模型的鲁棒性,减少噪声的影响,引入不敏感损失函数ε,此函数可以描述为:
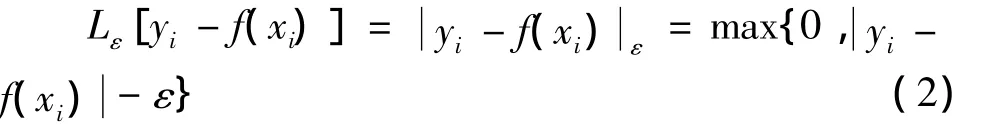

式中:K(xi,xj)为满足Mercer定理的内积核(核函数)。
引进核函数K(xi,xj)也是支持向量机理论的一个亮点,它将非线性不可分问题转化为线性可分问题来解决,避免了维数灾难并降低了算法的复杂性。常见的几种核函数有线性核、多项式核、高斯径向基核、Sigmoid核以及傅里叶核。
上述的对偶优化问题其实是二次凸规划问题,求解该二次凸规划问题即可得到最优解αi,α*i。因此线性回归函数模型可表示为:
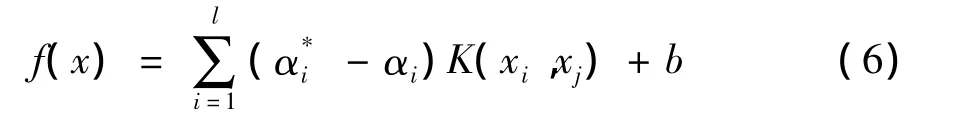
2 PSO原理
粒子群优化算法(Particle Swarm Optimization,PSO)是由Kennedy和Eberhart提出的一种基于群智能(Swarm Intelligence)的演化计算技术,是在鸟群、鱼群和人类社会的行为规律的启发下提出来的。粒子群优化算法通过群体中的粒子间的合作与竞争产生的群体智能来指导优化搜索。与演化计算相比,PSO保留了基于种群的全局搜索策略,它采用的速度-位移模型操作简单,避免了复杂的遗传操作。粒子群优化算法特有的记忆,使其可以动态跟踪当前的搜索情况,调整其搜索策略。与演化计算相比,粒子群优化算法是一种高效的并行搜索算法。由于算法收敛速度快,设置参数少,近年来受到学术界的广泛重视[6]。
粒子群优化算法的精确描述为:在D维目标搜索空间中,n个粒子组成一个群落,每个粒子i包含一个D维的位置向量xi=(xi1,xi2,…,xiD)和速度向量vi=(vi1,vi2,…,viD)。粒子 i在搜索D维解空间时,记住其搜索到的最优位置pi。在每次迭代中,粒子 i根据自身惯性、自身经验 pi=(pi1,pi2,…,piD)和粒子群最优经验 pg=(pg1,pg2,…,pgD)调整自身的速度向量,进而调整自身位置。可以通过一个适应值函数f(x)来衡量粒子的优势[6]。
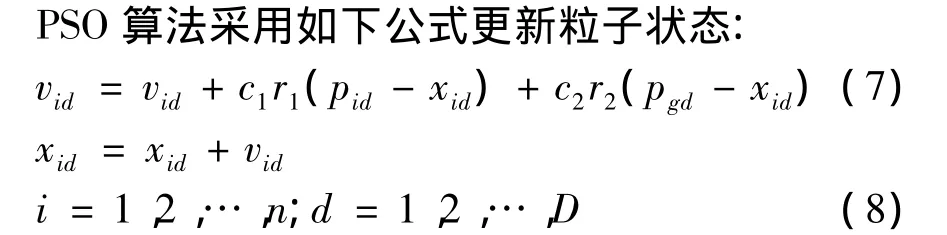
式中:学习因子c1和c2是非负常数;r1和r2是取值介于(0,1)之间的随机数;vid∈[-vmax,vmax](vmax是常数,根据具体问题而设定)。
3 基于PSO-SVM交通流量预测建模
交通流量预测是根据交通流量历史数据和现在数据,采用一定的方法建立合适的数学模型,然后用该模型对未来交通流量进行预测。支持向量机在预测推广方面具有优势,但支持向量机在学习训练时参数的选择没有具体的理论可依,严重影响了支持向量机模型的预测效果和效率。人工的设定参数,往往是根据具体的问题,多次选择参数,通过比较确定较优的参数组合。人工选择设定参数的方法效率低,盲目性大,因此采用群体智能算法对支持向量机模型的参数进行优化。文献[5]采用了遗传算法对支持向量机模型的参数进行优化选择,但是遗传算法程序复杂,参数设置较多,收敛速度慢,影响了模型的预测效率。而粒子群优化算法算法程序实现简单,设置的参数少,收敛速度比较快。因此采用PSO-SVM预测模型对交通流量进行预测分析。
PSO-SVM预测模型的算法步骤为:
1)建立训练样本集。采集某时间段内交通流量数据,构造训练样本 (X,y)={(xi,yi)|i=1,…,n},其中 xi=(ai,ai+1,ai+2,ai+3,ai+4)为第 i个样本点的输入向量,yi=ai+5为对应的第i个输出值。
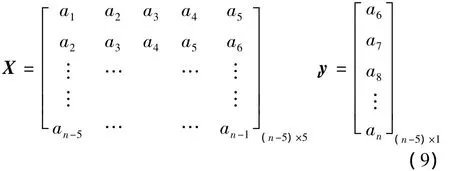
2)PSO的初始化。设置PSO的初始参数,如群体规模N,学习因子c1和c2等。在允许的范围内,随机的生成粒子的初始位置和初始速度。
3)确定支持向量机的参数C和σ2取值范围。
4)用训练样本集训练SVM,并计算各个粒子的适应度函数值,将其适应值与其经历过的最好位置pbest进行比较分析。如果优于pbest,则将其作为当前的最好位置pbest。笔者采用平均相对误差作为适应度函数,具体形式如下:
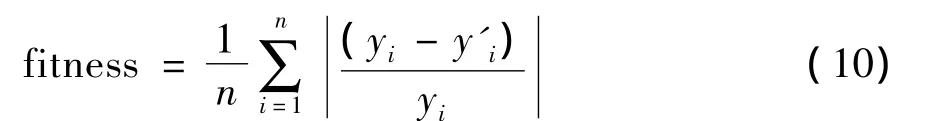
式中:n为训练样本点的数目;yi是第i个样本的实际值;y'i为第i个样本的预测值。
5)对每个粒子,将其适应值与所有群体粒子所经历过的最好位置的适应值进行比较,若小于所有群体经历过的最好位置的适应值,则全局最优位置gbest被当前粒子的最优位置所替代。
6)根据式(7)、式(8)更新当前粒子的位置和速度。
7)判断终止条件。判断全局最优位置的适应值是否满足设定的最小适应阈值或者是否达到最大的迭代次数。若满足终止条件,则输出最优解C和σ2,算法结束。否则返回步骤2)。
8)将最优解C和σ2代入SVM模型,重新训练学习,得到较优的SVM预测模型。

图1 PSO-SVM交通流量预测模型的优化寻参过程Fig.1 The process of searching parameters for PSO-SVM model
4 实例仿真
选取文献[7]中12:45—14:40期间记录的24组数据作为实验数据(表1),将其中12:45—14:20期间记录的20组数据作为模型的训练学习样本集,14:25—14:40期间记录的4组数据作为模型的测试样本集。实验程序在MATLAB7.1平台上编写,程序调用了比利时鲁汶大学电子工程系版的SVM(LSSVMlab1.5)工具箱和Brian Birge版粒子群优化工具箱。4
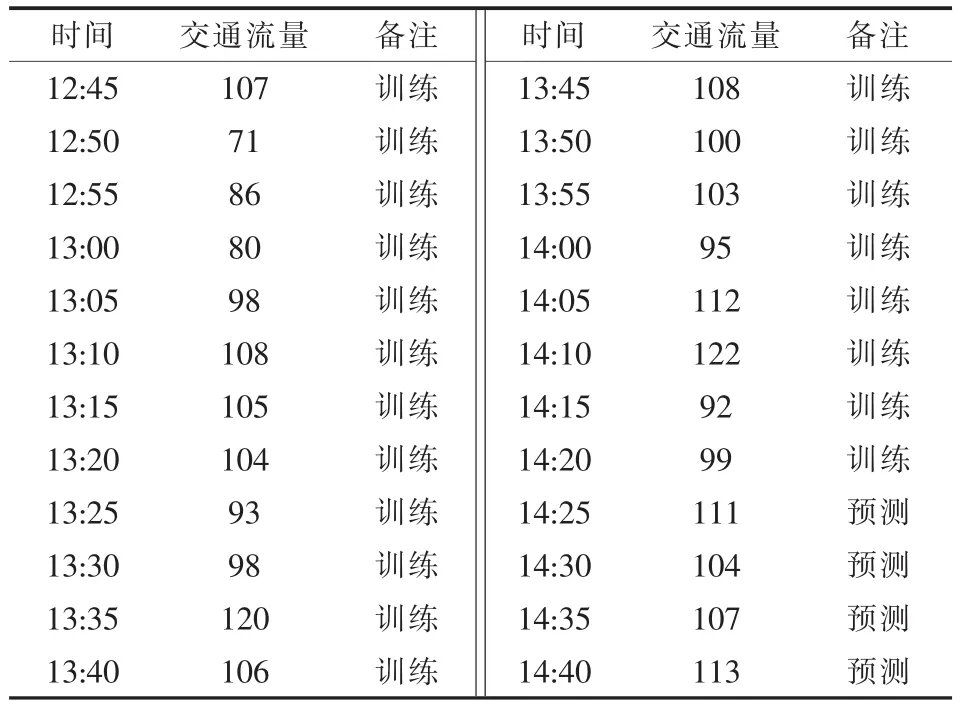
表1 路口A 12:45—14:40期间记录的24组流量数据[7]Table 1 24 couples of data of traffic flow between 12:45 and 14:40 at the intersection A /(veh·h-1)
.1 PSO-SVM交通流量预测模型
首先,将表1中流量数据进行归一化,采用的归一化处理公式为:
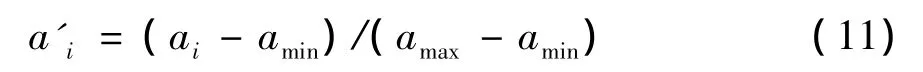
式中:a'i为归一化后的数据;ai为原始数据;amin和amax分别为原始数据中的最小值和最大值。然后构造训练样本集,采用嵌入维数为5,即输入数据的维数为5,所得训练样本集的形式如式(9)。
设置PSO-SVM模型的参数值及参数取值范围:粒子群规模为20;解空间为二维,分别对应C和σ2的取值,C ∈[0.01,500],σ2∈[0.01,10];最大迭代次数为2 000;加速因子c1=c2=2。经PSO优化选择得到较优的参数组合为C=150,σ2=0.01,然后将这两个参数代入SVM预测模型重新训练模型,继而得到经PSO优化的SVM预测模型。最后,利用测试样本集测试经PSO优化后的SVM模型,测试结果见表2。
4.2 神经网络预测模型
为了进一步作比较,同时利用BP神经网络预测模型和RBF神经网络预测模型分别对该组流量数据进行训练学习,并用测试样本集进行测试。BP神经网络预测模型采用的网络结构为“5-10-20-1”型,学习速率为0.01,训练最大次数为2 000。RBF神经网络预测模型采用3层的前向网络,激活函数采用高斯函数,均方差精度为0.002,散布常数为1。BP神经网络预测模型和RBF神经网络预测模型的测试结果如表2。
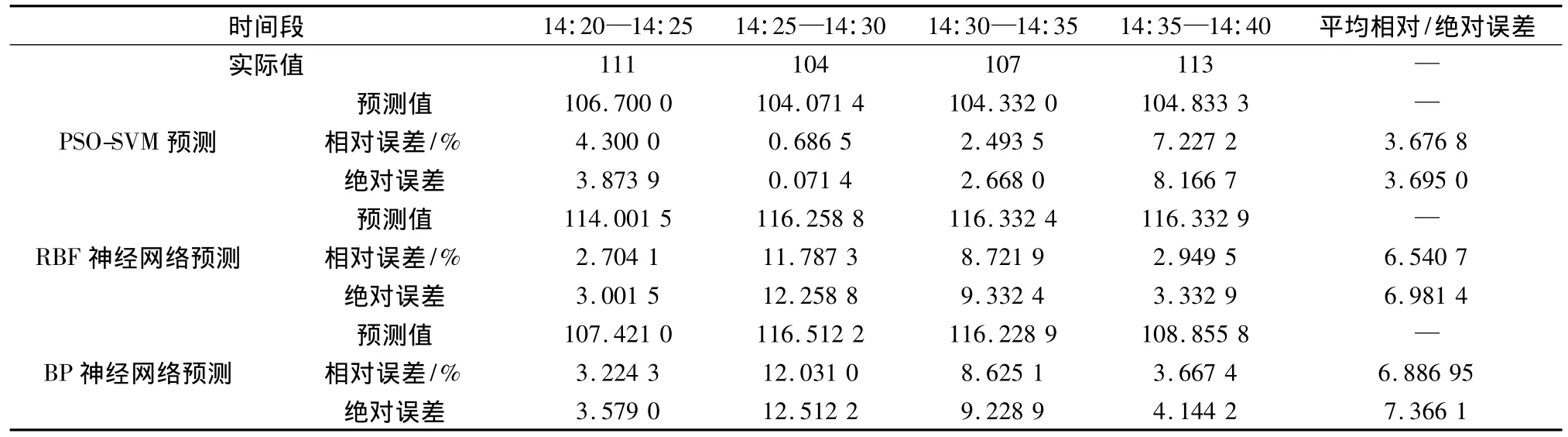
表2 PSO-SVM与RBF神经网络、BP神经网络预测结果的对比Table 2 Comparison of predicting outcomes among PSO-SVM,RBF neural network and BP neural network
4.3 模型的对比与分析
从表2可以看出,PSO-SVM预测模型的平均绝对误差和平均相对误差分别为3.695和3.676 8%。PSO-SVM预测模型在预测的平均相对误差和平均绝对误差上,明显的小于BP神经网络预测模型、RBF神经网络预测模型的预测误差。因此,经PSO优化的SVM模型比神经网络预测模型具有更好的预测能力。
同时还发现,PSO-SVM预测模型14:40的预测值的相对误差为7.227 2%,误差超过5%,主要有两方面原因:①预测的时间段(14:20—14:40)稍长,造成了训练样本的有效性降低;②交通流量短时的多变性,复杂性,影响了短时预测的可靠性。
5 结语
PSO模型具有程序实现简单,设置参数少,计算收敛速度快等优点;SVM模型具有小样本学习能力,学习速度快,泛化能力强等优点。基于PSOSVM的预测模型,就是将PSO和SVM结合在一起,利用PSO优化选择SVM模型的参数,得到较优的SVM预测模型。通过实验结果表明,基于PSO-SVM模型的预测方法优于神经网络的预测方法,它克服了神经网络学习训练时的“过学习”现象,避免了局部最优解,具有极好的泛化能力。因此,基于PSOSVM的预测模型要好于单纯的SVM预测模型,它解决了SVM预测模型的参数选择问题。
[1]朱文兴.基于RBF神经网络的交通流量预测算法[J].山东大学学报:工学版,2007,37(4):23-27.
Zhu Wenxing.Traffic volume forecasting algorithm based on RBF neutral network[J].Journal of Shandong University:Engineering Science,2007,37(4):23-27.
[2]温惠英,李俊辉.基于改进支持向量机的交通流量预测算法研究[J].交通与计算机,2008,26(2):4-7.
Wen Huiying,Li Junhui.Traffic flow prediction algorithm based on improved support vector machine[J].Chinese Journal of Computer and Traffic,2008,26(2):4-7.
[3] 方瑞明.支持向量机理论及其应用分析[M].北京:中国电力出版社,2007:47-49.
[4] 任洪娥,霍满东.基于PSO优化的SVM预测应用研究[J].计算机应用研究,2009(3):867-869.
Ren Honge,Huo Mandong.Support vector machine optimized by particle swam optimization algorithm for holding nail force forecasting[J].Chinese Journal of Computer Application Research,2009(3):867-869.
[5]李晓斌.基于遗传算法优化支持向量机的交通流量预测[J].微电子学与计算机,2010,27(10):186-189.
Li Xiaobin.Forecasting urban traffic flow based on support vector machine optimized by genetic algorithm[J].Chinese Journal of Microelectronics and Computer,2010,27(10):186-189.
[6]段晓东,刘向东.粒子群算法及其应用[M].沈阳:辽宁大学出版社,2007:29-34.
[7] 胡佩锋.交通流量短时预测方法研究[D].北京:北京交通大学,2006:44-45.
[8]侯媛彬,杜京义,汪梅.神经网络[M].西安:西安电子科技大学出版社,2007:89-122.
[9]刘丽娜.城市道路交通流量短时预测的研究[D].北京:北京邮电大学,2009:40-46.
Short-Time Prediction of Traffic Flow on the Basis of PSO-SVM
Wang Shuyang,Huang Tianmin,Fang Xin
(College of Mathematics,Southwest Jiaotong University,Chengdu 610031,Sichuan,China)
Parameter selection for SVM exerts influence on the predicting function of SVM prediction model in traffic flow.The present paper introduces PSO optimization mechanism to solve parameter selection of SVM.The way is to select SVM training parameters by PSO;then better PSO-SVM prediction model is obtained.Finally the paper compares PSO-SVM prediction model with neural network by means of simulation experiments and shows that PSO-SVM prediction model has advantages over neural network.
support vector machine(SVM);particle swarm optimization(PSO);neural network;prediction;traffic flow
U491.1+12
A
1674-0696(2012)04-0832-04
10.3969/j.issn.1674-0696.2012.04.24
2011-11-28;
2012-03-16
国家自然科学青年基金项目(61100046);四川省应用基础研究计划项目(2011JY0092);中央高校科研业务费专项资金项目(SWJTU11ZT29)
王树洋(1986—),男,山东泰安人,博士研究生,主要从事机器学习、人工智能方面的研究。E-mail:swjtusywang@163.com。

