A Stochastic Study on the Wicking Phenomena

WENG Ming(翁 鸣)，LUKAS David

1 Key Laboratory of Advanced Textile Materials and Manufacturing Technology，Ministry of Education，Zhejiang Sci-Tech University，Hangzhou 310018，China

2 Faculty of Textile Engineering，Technical University of Liberec，Liberec 46117，Czech

Introduction

Wicking phenomena plays an important role in application fields such asunderground watercontrol，papermaking，composite fabrication，and textile finishing［1-3］.Underlying the complexity of real systems，the inherent physics of wicking phenomenon can be regarded as the replacement of gas with liquid into the interspaces constructed by solid materials.

A classical theory of wicking in a cylindrical capillary is the equation proposed by Washburn［4］.It was pointed out that，in the derivation of the Washburn equation，the capillary force was assumed to be the unique driving force forwicking［4-6］.However，this assumption is valid only when a precursor film of the liquid exists ahead of the flow front，otherwise，an additional driving force is available from the change of the solid surface free energy，which altersthewicking dynamics.Therefore，a modified model by considering the spreading pressure was proposed by Good［5］，while Chibowski et al.analyzed the effect ofthe additional force under four distinct experimental conditions［6］.

Besides the Washburn equation and its modified forms，stochastic models originated from the Ising model have also aroused great interest in the study of wicking phenomena.The Ising model was proposed to solve ferromagnetic problems regarding phase transition and critical phenomena［7，8］.The remarkable feature of the Ising model lies in its simplicity and exact solution of the issues in one-and two-dimension.

Since 1980's，the Ising model has been extensively used to study the equilibrium properties and phase transitions with respect to the motion of a droplet on a planar solid surface［9-13］.Based on Manna's study［13］，Lukas et al.proposed a modified Ising model combined with Monte Carlo method to mimic the scenarios of liquid wicking in homogeneous fibrous network［14，15］as well as in fiber bundles［16］.Assuming that the dominant interactions between liquid-liquid and liquid-solid phases are apolar，Zhong et al.introduced Lifshitz-van der Waals theory to characterize the interaction energies in the spin system and studied the wicking dynamics of water in fibrous assemblies［17］.A model in consideration of polar interactions was developed in our previous study［18］.Since the Ising model is restricted to twophase systems，when it is applied to the three-phase wicking system composed of air，liquid，and solid，an additional spin variable or two sets of spin variables are required.

In this paper，we will propose a stochastic approach based on the Potts model which is a generalized Ising model readily to describe multiphase systems.Both apolar and polar interactions are incorporated into the model so that it is applicable to the study of wicking behavior resulted from diverse gas-liquid-solid coupling interactions.An experimental verification of the model is also reported.

1 Model Description

In this section，we will develop a stochastic approach based on the Potts model and Monte Carlo method to study the properties of wicking systems in thermodynamic equilibrium.

The Potts model is a generalization of the Ising model.A 3-state Potts model is constituted by spins each taking on one state or one of three disparate spin values.The Hamiltonian of the Potts model is formulated as［10］

A wicking system is a three-phase system hence could be studied by a 3-state Potts model.A 3D 3-state Potts model consisting of L×W ×H cubic cells is illustrated in Fig.1.Each of the cells represents a“spin”and is assigned with a spin value σi=0，1，or 2，denoting its state of being exclusively occupied by gas，liquid，or solid.For simplicity，the spin values 0，1，and 2 are used as subscripts in the following text.A gravitational field is applied to the system in negative z-direction.

The Hamiltonian of the wicking system is assumed to be the total potential energy pertinent to the nearest neighboring spinspin interaction on mutual interface，and the spin-external field interaction on the center ofeach spin.Therefore，the Hamiltonian of the system in Fig.1 can be expressed as

where J is a 3 ×3 coupling constant matrix with elements J(σi，σj)denoting the strength of potential energy per unit area between pair spins(σi，σj)and Aijis the interaction area;k1is a coefficient accounting for the discretization of the real system;G(σi)is the intensity of the gravitational filed at vertex i;and zithe coordinate of spin i in z direction.The first summation runs over all nearest neighboring spin pairs in the system and each pair for once，while the second runs over all individual spins.

The constant G( σi)is defined as G(σi)= ［δσi，0ρ0+δσi，1ρ1+ δσi，2ρ2］g · dV，where ρ0，ρ1，and ρ2are the densities of gas，liquid，and solid，g is the gravitational acceleration，g=9.8 m/s2，and dV is the volume of one unit cell.

The coupling constant matrix J is defined as the strength of potential energies resulted from the interactions between the nearest neighboring spin pairs which can be evaluated via the energy change during a thermodynamic process.We assume that the interaction from gas spin is week enough to be neglected，i.e.，J(0，0)=0，and J is a symmetric matrix with J(σi，σj)=J(σj，σi).Therefore，the interaction energy for two combined phase σiand σj(σi≠σj)is the adhesion energy，which is equal to the energy change during an isothermal formation of a unit interface.So we have

In the case of σj= σi，the interaction energy turns into cohesion energyand Eq.(4)reduces to

By simultaneously solving Eqs.(4)and(5)，all elements J(σi，σj)in matrix J can be determined.Among the infinite solutions，we assume，in this paper，

where γσi，σjis the interfacial free energy on unit area between pair spins(σi，σj)and δ is the Kronecker delta.

Equation(5)implies that the interfacial potential energy is herein assumed to be the interfacial free energy，or the energy excess resulted from the unbalanced forces on both sides of the interface.

By substituting Eq.(5)into Eq.(2)，we obtain the formula of the Potts model

In the application of the modified Potts model described by Eq.(7)，energy contributions of both aploar and polar spin-spin interactions are to be considered.According to the theory proposed by Fowkes［19］and Good［20］，the interfacial free energy between phases σiand σj( σi，σj∈{0，1，2})can be broken down into its separate components

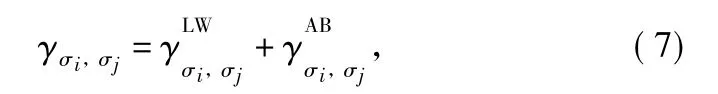
where the superscript LW and AB represent the apolar Lifshitzvan der Waals interaction and the polar electron acceptor-electron donor or Lewis acid-base interaction，respectively.For condensed phases，the cohesion energy of phase σi( σi∈ {1，2})is calculated by equation

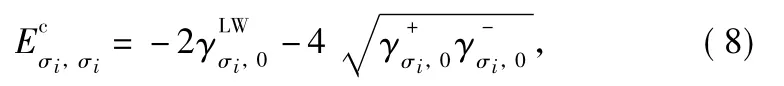
With Eqs.(6)-(9)，the change in Hamiltonian accompanying wicking process involving apolar and polar components can be well determined.

In addition to the change in Hamiltonian，the apparent curvature of the liquid surface will change the thermodynamics of wickingby causing an additionalenergy change in the process［20］.This extra energy change is introduced here as the work done by external pressure p to the system.

where k2is a coefficient for the discrete system as k1;dV is the volume of a unit cell;dA is the variation in the area of liquid surface.

To sum up，the total energy change of the spin system accompanying the wicking process is

The evolution of the spin system corresponding to the wicking process is assumed to be a stochastic process.According to Metropolis，it may be realized by an importance sampling scheme along a Markov chain constructed in the phase space.Each state of the system is described by a set of spin variables xi=(σ1，σ2，… ，σN)and correlates only with the previous state xi－1.The transition probability of the system from state xito the next xi+1depends on the energy difference between the two states and can be expressed as

where β is a constant.

In this paper，we restrict our study to the equilibrium wicking height of the liquid column in a cylindrical capillary.In terms of the criterion described by Eq.(12)，the spin system changes its states until it reaches an equilibrium state when the maximum height of the liquid spins fluctuates about a mean value.

2 Materials and Methods

To verify the model developed above，vertical wicking experiments of four liquids in a set of capillaries were performed.The radii of the capillaries were in the range of 0.17-1.35 mm.Two apolar liquids(heptane，octane)and two polar liquids(water，formamide)were selected to constitute different coupling interactions in the wicking system.The materials used for experiments including commercial glass capillary for viscometer，distilled water，analytical grade heptane，octane，formamide werepurchased from localcompanies in Shanghai.The specifications of the liquids were taken from Refs.［21，22］as summarized in Table 1.

Table 1 The specifications of the testing liquids

The radii of capillaries were determined by a photographic technique.Photos of capillary cross-sections(×50 times)were taken by an electron microscope.Eight groups of data of radius were recorded for each capillary cross-section with 45 degree intervals and the average values were used for subsequent calculation.Before the wicking experiment，the capillaries were cleaned by distilled water，dried at 150℃ for 2 h and then kept in a desiccator for 24 h at room temperature(20℃).Each capillary was held vertically on a frame with the lower end dipping into a liquid reservoir.The equilibrium height of the liquid column in the capillary was recorded.All the experiments were performed at room temperate(20±2)℃.

3 Simulation and Discussion

In the simulation，the spin system is created by generating coaxial cylindrical ring unit cells with the same volume.In such a system，the radial thickness of the cell decreases with the increasing distance to the central axis.Each cell is assigned with a spin variable σi=0，1，or 2 according to its phase state.The outmost cell represents the capillary wall，and the bottom of the system is filled with liquid.The system is divided into 8×1 500 cells for all the simulations.The radical dimensions of the cells are calculated from the radii of the testing capillaries and the height of each cell represents 0.1 mm in the real system.

The parameters used in the simulation are listed in Table 2.The cohesion energies of the liquids are calculated from the data in Table 1 via Eq.(9)and the adhesion energies are decided experimentally by Eq.(10).

Table 2 Parameters used for simulation

It should be noted that for strong polar liquid such as water，polar AB interaction contributes 120 mJ/m2to the total cohesion energy 145.6 mJ/m2.Therefore，when considering interaction energies in a wicking system involving water，the energy contributions from polar interactions could not be neglected.

The simulation results as well as the experimental results are shown in Fig.2.All the simulations are carried out at β =2.5.The coefficients k1=1.07 and k2=1.00 are determined by the simulation to accommodate the experimental data of water and heptane.The height of the central cell is recorded as the wicking height of the liquid and the equilibrium height is taken to be reached after it fluctuates within the range of 0.2 mm for 107spin flip trials.An average of equilibrium wicking height is obtained from 103spin flip trials.Then，the wicking heights of formamide and octane are predicted at the same condition.

Figure 2 shows that the simulation results agree well with the experimental results.An equilibrium wicking height is reached for each experiment，which indicates that the effect of gravity can not be neglected in the case of vertical wicking.The equilibrium wicking height decreases with increasing capillary radius，but varies in a distinctive way for each liquid.By considering both apolar and polar interactions in the system and the work done by externalpressure，the stochastic modelcan describe the equilibrium wicking height of liquids with different properties.

The results above reveal the advantages of the proposed approach.It describes the intricate interactions involved in a three-phase system in a simple form，yet yields realistic results.And，the parameters in the model have clear physical meanings.After deciding the parameters from two testing liquids，the model can be used to predict the wicking behavior of liquids with different properties.

The proposed technique provides useful information of the mechanisms of wicking behavior and also a useful tool for studying more practical issues with respect to wicking phenomena.

4 Conclusions

In this paper，a stochastic approach based on 3D 3-state Potts model with combination of Monte Carlo method is proposed to study the phenomena of liquid wicking in capillaries.In the model，the potential energy between spins is characterized by interfacial free energy.Both apolar Lifshitz-van der Waals interaction and polar acid-base interaction are considered for six types of interactions between two of the three phases:gas，liquid，and solid.The work done by the external pressure is also taken into account as the effect of the curvature of the liquid surface on the thermodynamics of wicking.

The dynamics of wicking is viewed as the replacement of gas with liquid inside the capillary，which is governed by the difference in total energy of the spin system for two consequent states.The equilibrium height is the balance between the driving force and the gravity.The modelisverified bywicking experiments of apolar and polar liquids in capillaries of different radii.The good agreement between simulation and experimental results shows that the new model is an attractive tool in this area and it may be used for studying more practical issues.

［1］Fan Z S，Neff J C，Harden J W，et al.Water and Heat Transport in Boreal Soils:Implications for Soil Response to Climate Change［J］.Science of the Total Environment，2011，409(10):1836-1842.

［2］Nithya E，Radhai R，Rajendran R，et al.Synergetic Effect of DC Air Plasma and Cellulase Enzyme Treatment on the Hydrophilicity of Cotton Fabric［J］.Carbohydrate Polymers，2011，83(4):1652-1658.

［3］Park C H，Lebel A，Saouab A，et al.Modeling and Simulation of Voids and Saturation in Liquid Composite Molding Processes［J］.Composites Part A:Applied Science and Manufacturing，2011，42(6):658-668.

［4］Washburn E W.The Dynamics of Capillary Flow［J］.Physical Review，1921，17(3):273-283.

［5］Good R J.The Rate of Penetration of a Fluid into a Porous Body Initially Devoid of Adsorbed Material(1，2)［J］.Journal of Colloid and Interface Science，1973，42(3):473-477.

［6］Chibowski E，González-Caballero F.Theory and Practice of Thin-Layer Wicking［J］.Langmuir，1993，9(1):330-340.

［7］Ising E.Beitrag zur Theorie des Ferromagnetismus［J］.Zeitschrift fur Physik，1925，31(1):253-258.

［8］Lim C，Nebus J.Vorticity，Statistical Mechanics，and Monte Carlo Simulation［M］.New York:Springer Science+Business Media，LLC，2007.

［9］Abraham D B.Solvable Model with a Roughening Transition for a Planar Ising Ferromagnet［J］.Physical Review Letters，1980，44(18):1165-1168.

［10］Selke W.Droplets in Two-Dimensional Ising and Potts Models［J］.Journal of Statistical Physics，1989，56(5/6):609-620.

［11］de Coninck J，Dunlop F.Wetting Phenomena［M］.New York:Springer-Verlag Berlin Heidelberg，1988:29-39.

［12］Binder K.The Monte Carlo Method in Condensed Matter Physics［M］.2nd ed.New York:Spinger-Verlag，1992:329-354.

［13］Manna S S，Herrmann H J，Landau D P.A Stochastic Method to Determine the Shape of a Drop on a Wall［J］.Journal of Statistical Physics，1992，66(3/4):1155-1163.

［14］Lukas D，Glazyrina E，Pan N.Computer Simulation of Liquid Wetting Dynamics in Fiber Structures Using the Ising Model［J］.Journal of the Textile Institute，1997，88(2):149-161.

［15］Lukas D，Soukupova V，Pan N，et al.Computer Simulation of 3-D Liquid Transport in Fibrous Materials［J］.Simulation，2004，80(11):547-557.

［16］Lukas D，Pan N.Wetting of a Fiber Bundle in Fibrous Structures［J］.Polymer Composties，2003，24(3):314-322.

［17］Zhong W，Ding X，Tang Z L.Modeling and Analyzing Liquid Wetting in Fibrous Assemblies ［J］.Textile Research Journal，2001，71(9):762-766.

［18］Weng M，Ding X.The Effect of Surface Free Energy of Liquid on Wicking in a Fiber Bundle［C］.Proceedings of the 2nd International Textile Clothing ＆ Design Conference，Dubrovnik，Croatia，2004:467-470.

［19］Fowkes F M，Mostafa M A.Acid-Base Interactions in Polymer Adsorption［J］.Industrial Engineering Chemistry Product Research and Development，1978，17(1):3-7.

［20］Good R J，van Oss C J.The Modern Theory of Contact Angles and the Hydrogen Bond Components of Surface Energies［M］//Schrader M E，Loeb G I.Modern Approaches to Wettability，Theory and Applications.New York:Plenum Press，1992.

［21］Chibowski E.Solid Surface Free Energy Components Determinations by the Thin-Layer Wicking Technique［J］.Journal of Adhesion Science and Technology，1992，6(9):1069-1090.

［22］Lide D R.Handbook of Chemistry and Physics:a Ready-Reference Book of Chemical and Physical Data［M］.73rd ed.Boston:CRC Press，Inc.，1992.