转子全周碰摩与局部碰摩的识别方法研究

熊 炘，杨世锡，甘春标，周晓峰

(浙江大学 机械工程学系 流体传动及控制国家重点实验室，杭州 310027)

转子全周碰摩与局部碰摩的识别方法研究

熊 炘，杨世锡，甘春标，周晓峰

(浙江大学 机械工程学系 流体传动及控制国家重点实验室，杭州 310027)

超临界汽轮发电机组的结构和工况复杂，容易引起转、静子间的碰摩。根据碰摩诱发因素的不同，可将其分为全周碰摩与局部碰摩。由于两种碰摩故障的时、频特征相似，传统的时、频域分析方法很难准确提取它们的故障特征。针对这一不足，提出一种基于经验模式分解－奇异值分解(EMD－SVD)与支持向量机(SVM)的碰摩故障识别方法，用于对转子全周碰摩与局部碰摩故障进行识别。首先，通过EMD获取碰摩信号的固有模式函数(IMF);然后，提取表征信号主要能量的前四阶IMF组成特征矩阵并进行SVD分解，得到关于原信号的一组特征值;最后，将特征值输入SVM，对原信号进行分类识别。转子试验台全周碰摩与局部碰摩试验结果表明，该方法对转子全周碰摩与局部碰摩故障的分类准确率高，其中以径向基函数作为核函数的SVM分类准确率达到96.0%。

转子;全周碰摩;局部碰摩;经验模式分解;奇异值分解;支持向量机

随着我国淘汰落后产能、实现节能减排等重大战略的实施，大容量、高参数化的超临界汽轮发电机组在我国火力发电装备中所占的比例不断增加。较之于同容量的亚临界机组，超临界机组轴系跨数多、跨度大，冷、热态温度变化剧烈。与此同时，为了提高运行效率，这类机组的动静间隙往往控制在较小范围内。因此，超临界汽轮发电机组比一般亚临界机组更易发生转、静子之间的碰摩现象，必须加强对其运行状态的监测，及早发现并消除故障隐患。

转、静子之间的碰摩故障一般为机组的二次故障，其诱发因素多为转子不平衡量过大、轴系不对中、流体激励引起的轴系失稳等一次故障［1］。当一次故障使转子与碰摩点始终保持接触时，称为全周碰摩。Bently等［2］对转子与汽封的全周碰摩现象进行了系统的实验研究;Choi等［3］通过构建碰摩试验装置，对全周碰摩的机理进行了数值仿真研究;徐尉南等［4］采用带不平衡量的柔性静子－柔性单圆盘转子模型对同步全周碰摩现象进行了分析研究。当一次故障只使转子的部分弧段与碰摩点发生接触时，则为局部碰摩。Pennacchi等［5］分别利用试验模态分析和有限元建模方法对转子的早期局部碰摩现象进行了对比研究;王正浩等［6］分析了2圆盘、8自由度弹性转子局部碰摩时的分叉与混沌行为;Cheng等［7］提出了一种基于经验模式分解(Empirical Mode Decomposition，EMD)的转子局部碰摩故障诊断方法。从文献的梳理和对比分析中可以发现，多数转子碰摩的研究成果集中在对转子系统的数学建模和振动响应分析两方面，且只针对全周碰摩和局部碰摩两者中的一种进行单独研究，而将两种碰摩故障进行对比分析的研究工作很少。由于两种类型碰摩故障的振动信号极为相似，因此，如何从振动信号入手，正确识别碰摩故障的类型，对于确定碰摩位置，做出正确诊断决策至关重要。

Muszynska［1］指出，碰摩发生时转、静子之间同时存在摩擦、冲击、扭转和刚度耦合等四种效应。当发生全周碰摩时，摩擦效应占主导地位;而发生局部碰摩时，冲击效应占主导地位。因此，不同类型的碰摩故障，其能量分布也是不同的。本文通过EMD方法与奇异值分解(Singular Value Decomposition，SVD)方法［8－9］的有效结合，提取出原信号能量分布的特征值，从而获得表征原信号能量分布规律的特征参量。然后将经特征参量训练过的支持向量机［10］(Support Vector Machine，SVM)用于对不同类型的碰摩故障进行分类。对转子试验台上的碰摩仿真试验的应用结果表明，本方法能够有效区分全周碰摩与局部碰摩故障，且分类准确率高。

1 碰摩信号的EMD－SVD算法

碰摩信号特征提取算法首先对原信号进行EMD，得到一组固有模式函数(Intrinsic Mode Function，IMF)，然后提取前四阶IMF组成特征矩阵，最后利用SVD获得原信号的特征值，算法流程如图1所示。

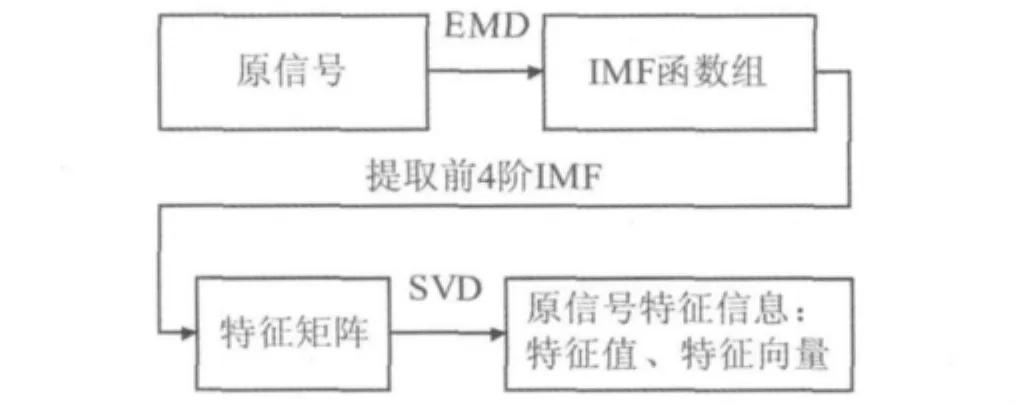
图1 碰摩信号特征提取算法Fig.1 Feature extraction algorithm for rub signals

1.1 EMD基本原理

在对原信号进行EMD时，首先需要搜索原始信号x(t)的所有极值点，然后应用三次样条曲线对所有极大值点和极小值点分别进行插值，获得x(t)的上、下包络线emax(t)和emin(t)。通过计算上、下包络线的均值：

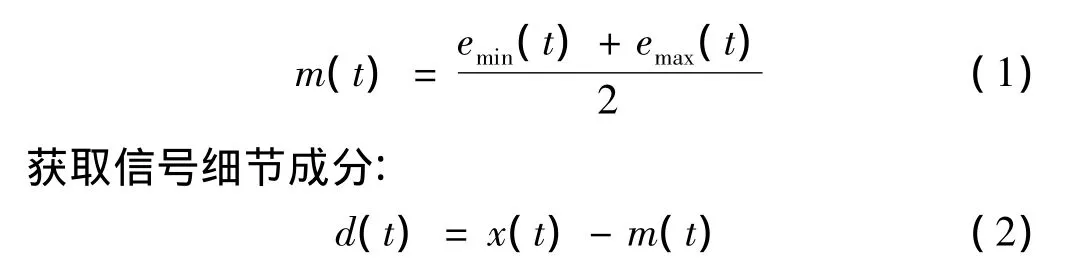
检查d(t)是否满足IMF条件：①对于某段时间序列，极值点和过零点数目必须相等或至多相差一点;②在任意点处由局部极大点和局部极小点构成的包络平均值为零。若d(t)满足以上两条件，则可判定d(t)为IMF;否则，需要重复计算包络线均值m(t)并提取信号细节成分d(t)，直至d(t)满足IMF条件。这时称d1(t)(d1(t)=d(t))为x(t)的一阶IMF。

进一步将d1(t)从x(t)中分离出去，可得余量：

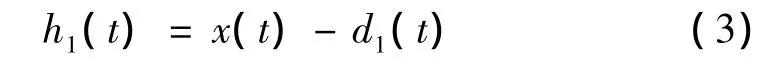
以h1(t)作为原始数据，重复执行上述步骤，直至分离出二阶IMF。以此类推，将x(t)分解为从高频到低频的若干阶IMF和趋势项：

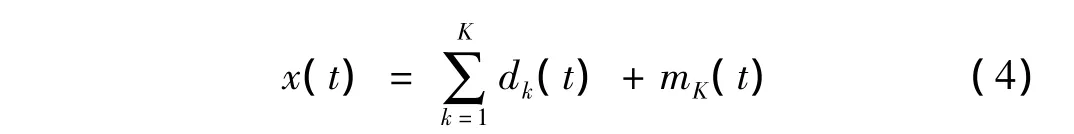
式中：dk(t)为第k阶IMF，mK(t)为趋势项，且dk(t)和mK(t)均为行向量。应用EMD后，全周和局部碰摩信号的前四阶IMF如图2(a)、图2(b)所示。

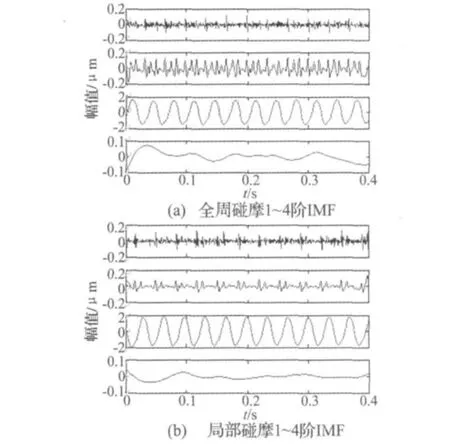
图2 碰摩信号1～4阶IMFFig.2 No.1～4 IMF of rub signal

1.2 SVD基本原理

利用EMD所得的前四阶IMF，组成关于原信号的特征矩阵：

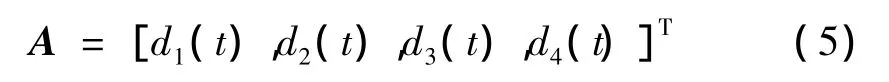
其中“［ ］T”为矩阵转置符号。

对于特征矩阵A∈Rm×n(m和n分别表示矩阵的行数和列数)，存在正交矩阵 U∈Rm×m和 V∈Rn×n

使得：

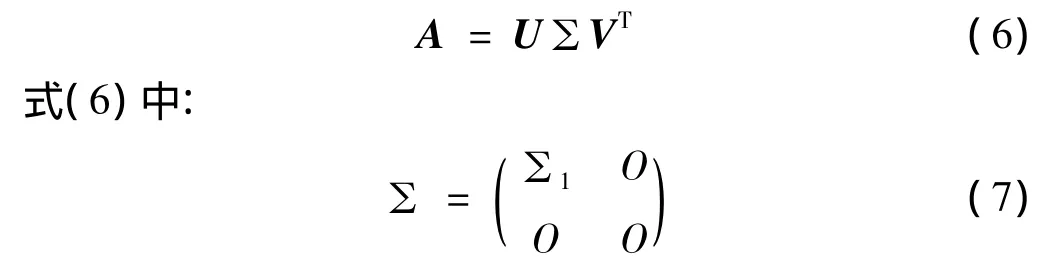
且∑1=diag(σ1，σ2，…，σr)，其对角元素 σi(i=1，2，…，r)为矩阵A的非零奇异值，排列顺序为σ1≥σ2≥…≥σr＞0，r=rank(A);U和V为酉矩阵，U和V的每列分别称为左、右奇异向量。σi的大小表示奇异向量在特征矩阵中贡献的大小。对于原信号的特征矩阵A，其特征值σi越大，表示相应奇异向量包含的关于原信号的信息越多;反之，则越少。∑1具有良好的稳定性，对于原信号中噪声的干扰免疫力强。因此，可将其作为原信号特征信息的重要参量，用作识别碰摩类型所用 SVM 的训练样本［8，10］。

2 碰摩类型的SVM识别算法

要应用SVM对转子碰摩类型进行识别，必须利用样本数据进行训练。

给定训练样本集合 D={(xl，yl)，l=1，…，L}(其中输入样本 xl∈Rd，类别标识 yl∈{+1，－1}，“+1”表示全周碰摩，“－1”表示局部碰摩)，对于两类线性可分的训练样本，存在一组超平面：

能将两类样本点完全分离。其中w为权重向量，b为偏置量。在这组超平面中，通过定义最优分类超平面，使得目标函数最小化：

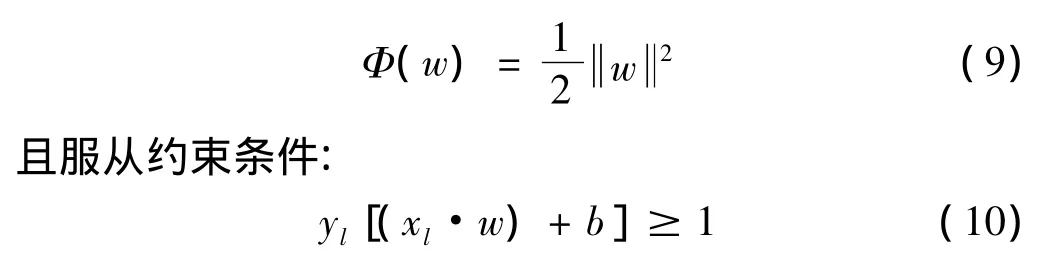
在大多数情况下，满足不等式(10)的最优超平面是不存在的。因此，引入松弛变量ξl＞0，则约束条件(10)变为：

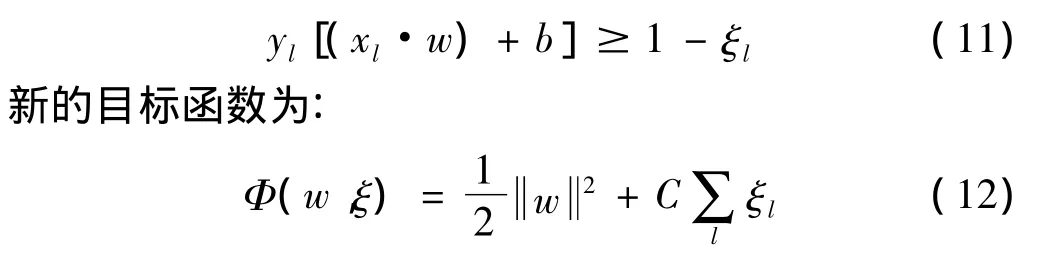
平衡因子C的值由用户定义，其作用是使得最近样本点到超平面的距离最大化以及分类误差最小化。

上述最优化问题式(11)～(12)的解变为：

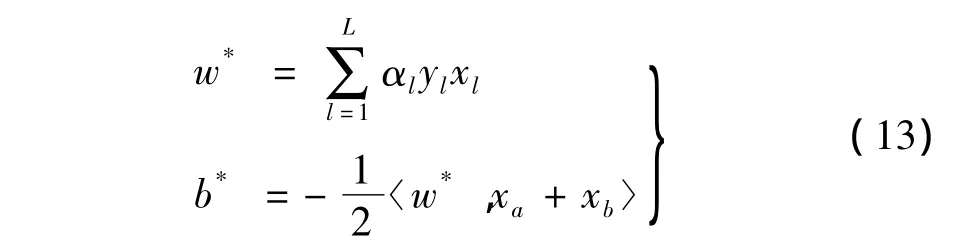
其中：αl为拉格朗日乘子，xa和xb为对应于αl≠0的两类碰摩样本数据中存在的支持向量，且有αa，αb＞0，ya=－1，yb=1。最后得最优分类器为：

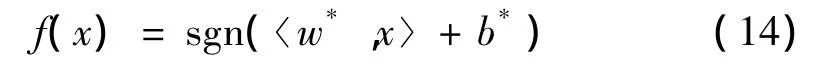
实际碰摩数据的分类问题往往属于非线性分类的范畴。因此，进一步引入核函数的概念，将样本空间映射到特征空间，然后在特征空间中进行线性分类，这样处理后所得最优分类器为：

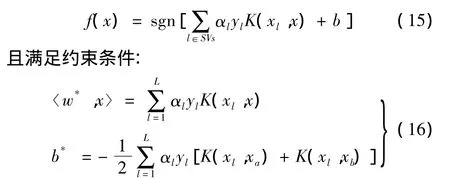
其中：SVs表示支持向量集合，K(x，x')为核函数。常用的核函数有线性核函数、多项式核函数和径向基核函数等。

3 碰摩分类试验分析

为了验证EMD－SVD与SVM相结合的碰摩故障识别方法对不同类型碰摩故障识别的有效性，本节利用Bently RK4转子试验台分别模拟转子的全周碰摩与局部碰摩故障，并使用训练完的SVM对碰摩故障进行分类测试。

3.1 试验台设置及参数选择

Bently RK4转子试验台如图3(a)所示。转子上安置左、右两个滑动轴承，转子中部安置调心框架一个，如图3(b)所示。调心框架左右约15mm处各固定一质量圆盘，用于保障高速运转条件下转子的稳定运行。调心框架上、左、右侧各安装一根弹簧，用于调节转子的轴心位置。此外，通过调节三根弹簧的拉力，使转子轴心与右轴瓦中心重合。

图3 Bently RK4转子试验台Fig.3 Bently RK4 test bench

全周碰摩通过图3(c)的方式模拟。通过控制盒调节转子运行状态，使转子在1 800 r/min的转速下平稳运行。将蜡棒通过人工按压的方式在运行转子上加载10 s，通过安装在转子试验台上的电涡流传感器以1 280 Hz的采样频率采集振动数据。从所采数据中每隔1 s选取时长为0.4 s的一组样本数据，共取50组样本数据。由于蜡棒刚度远低于转子系统，可认为转子系统发生了全周碰摩故障;局部碰摩装置如图3(d)所示，它由固定在支座上的碰摩支架与碰摩铜棒构成。转子启动前，铜棒与转子分离。转子启动后，将铜棒缓慢旋入支架螺纹孔直到与转子接触并保持一定的预紧力，然后将螺母旋紧，固定铜棒与支架的相对位置。由于铜棒的刚度与转子系统刚度接近，可认为这时转子系统发生局部碰摩。最后用相同方式采集局部碰摩样本数据50组。

3.2 试验结果分析

从50组全周碰摩样本数据和50组局部碰摩样本数据中各取一组进行EMD并画Hilbert时频谱，如图4所示。图4(a)和图4(b)分别为转子全周碰摩与局部碰摩振动信号的Hilbert时频谱，可以看到两类碰摩故障的时频特征十分相似，很难通过传统的时、频域及时频分析方法将它们区分开。因此，接下来应用EMDSVD与SVM相结合的方法对两种碰摩故障数据进行识别。

图4 碰摩信号Hilbert时频谱Fig.4 Hilbert spectrogram of rub signal

首先，通过随机排序的方法，将50组全周碰摩数据和50组局部碰摩数据混合成100组转子碰摩数据。然后，任取其中50组，通过EMD－SVD对其进行故障特征提取，将所得特征值输入SVM进行训练。试验所用SVM采用线性、多项式和径向基三种核函数分别对训练样本进行学习。每种核函数中所用参数的选择依据参考文献［11］。取其中最优结果列于表1第二列。将训练完的SVM用于剩余50组碰摩数据的分类测试，并以式(17)作为衡量分类准确率的指标。

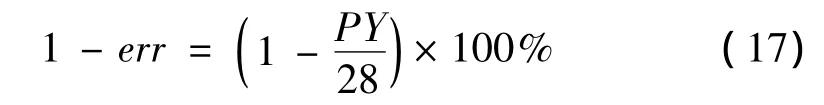
其中：err表示分类错误率，PY为碰摩数据被SVM分类后与实际所属碰摩类别不符的样本数据个数。

为了保证分类结果稳定性，本试验对100组混合后的碰摩数据再进行4次50组训练样本的随机提取，将5次试验所得分类准确率求平均值，其结果见表1第三列。由表可知，线性函数的分类准确率为86.3%，分类效果一般。而多项式函数和径向基函数的分类准确率都在94%以上，对全周碰摩与局部碰摩的分类效果十分理想。其中，分类结果最为准确的是以C=80，σ=10的径向基函数为核函数的SVM，分类准确率达到96.0%。

表1 不同核函数的分类效果Tab.1 Classification efficiency of different Kernel functions

4 结论

转子全周碰摩与局部碰摩信号的故障特征相似，用传统的时、频域特征提取方法很难将它们区分开。本文提出了一种基于EMD－SVD与SVM的故障识别方法，即：首先，从采集的碰摩信号中选取一部分信号，利用EMD将碰摩信号分解为IMF函数组;然后，提取表征信号主要能量分布的前4阶IMF组成信号特征矩阵，进而对该矩阵进行SVD，得到原信号的特征值并用其训练SVM;最后，将训练完的SVM用于剩余碰摩信号的分类试验。基于转子试验台全周碰摩与局部碰摩的试验结果表明，EMD－SVD与SVM的碰摩故障识别方法是有效的，对于两种不同类型碰摩故障的分类准确率高。其中，以径向基函数为核函数的SVM分类准确率达到96.0%。

需要指出的是，由于转子系统在不同工况下的刚度存在较大变化，因此，分别利用蜡棒和铜棒模拟全周碰摩与局部碰摩与实际情况存在一定偏差，今后需要专门建立一套精确模拟全周碰摩与局部碰摩的试验装置;此外，超临界汽轮发电机组结构和工况都较为复杂，对机组碰摩故障的机理进行分析对于全周碰摩与局部碰摩故障的区分意义重大。

［1］Musznska A.Rotor－to－stationary element rub－related vibration phenomena in rotating machinery：Literature survey［J］.The Shock and Vibration Digest，1989，21(3)：3 － 11.

［2］ Bently D E，Yu J J，Goldman P，et al.Full annular rub in mechanical seals， Part Ⅰ：Experimental results［J］.International Journal of Rotating Machinery，2002，8(5)：329－336.

［3］ Choi Y S.Dynamics of rotor rub in annular clearance with experimental evaluation［J］.Journal of Mechanical Science and Technology，1994，8(4)：404 －413.

［4］徐尉南，张 文，许 斌.柔性转子－柔性静子系统的同步全周碰摩分析［J］. 振动与冲击，2007，26(2)：1 －5，9.

［5］Pennacchi P，Bachschmid N，Tanzi E.Light and short arc rubs in rotating machines：Experimental tests and modelling［J］.Mechanical Systems and Signal Processing，2009，23(7)：2205－2227.

［6］王正浩，袁惠群，范改燕.考虑轴初弯曲时转子系统局部碰摩的分叉与混沌行为［J］.机械设计，2008，25(2)：37－41.

［7］ Cheng J S，Yu D J，Tang J S，et al.Local rub－impact fault diagnosis of the rotor systems based on EMD［J］.Mechanism and Machine Theory，2009，44(4)：784 －791.

［8］ Vanlanduit S，Parloo E，Cauberghe B，et al.A robust singular value decomposition for damage detection under changing operating conditions and structural uncertainties［J］.Journal of Sound and Vibration，2005，284(3 －5)：1033 －1050.

［9］段向阳，王永生，苏永生.基于奇异值分解的信号特征提取方法研究［J］. 振动与冲击，2009，28(11)：30－33.

［10］ Gunn S R.Support vector Machines for classification and regression［R］.Southampton：Image Speech and Intelligent Systems Research Group，University of Southampton，1997.

［11］ Ai L M，Wang J，Yao R X.Classification of parkinsonian and essential tremor using empirical mode decomposition and support vector machine［J］.Digitial Signal Process，2011，21(4)：543－550.

［12］李录平，卢绪祥.汽轮发电机组振动与处理［M］.北京：中国电力出版社，2007.

Recognition method for rotor system under full annular rub and partial rub

XIONG Xin，YANG Shi－xi，GAN Chun－biao，ZHOU Xiao－feng
(Department of Mechanical Engineering＆The State Key Lab of Liquid Power Transmission and Control，Zhejiang University，Hangzhou 310027，China)

Supercritical steam turbosets are highly complex in their structure and always run under various complicated working conditions.They are prone to rub between static and dynamic parts.Induced by different factors，rubbing faults can be divided into full annular rub and partial rub.Since the time－frequency characteristics of both are similar to each other，discrimination of the two kinds of rub faults is hard to proceed by using the traditional spectrum analysis methods.In response to make up for this shortage，an intelligent recognition method based on the EMD－SVD and SVM was proposed.IMFs were collected through EMD and the first－four－order IMFs，which contain the main power of the original signal，were extracted to form the characteristic matrix.The SVD was applied to obtain a series of eigenvalues，which were then inputted to train the SVM in order to classify rub faults.The newly developed intelligent recogonition method was used to analyze the signals collected from rotor test－bed under both full annular rub and partial rub conditions.The experiment results show that，classification accuracy of the method is high，especially for the SVM using radial basis as kernel function，where the classification accuracy is up to 96.0%.

rotor;full annular rub;partial rub;empirical mode decomposition(EMD);singular value decomposition(SVD);support vector machine(SVM)

TN911.7;TH165.3

A

国家自然科学基金(11072214);国家“863”高技术研究发展计划(2008AA04Z410)

2011－03－25 修改稿收到日期：2011－07－26

熊 炘 男，博士生，1983年11月生