滚珠丝杠副系统抗共振特性分析*
刘 立,汤文成,陈勇将
(东南大学机械工程学院,南京 211189)
滚珠丝杠副系统抗共振特性分析*
刘 立,汤文成,陈勇将
(东南大学机械工程学院,南京 211189)
为了提高高速运动滚珠丝杠副系统的稳定性,避免结构共振,对滚珠丝杠副系统的模态特性进行有限元分析。探讨了螺母位置、支撑方式、工作台及两端支撑轴承对滚珠丝杠副系统模态特性的影响。最后,通过锤击法对滚珠丝杠副系统进行试验模态分析。结果表明:不同的需求场合需选择不同的支撑方式。工作台质量以及轴承的轴向刚度均影响进给系统的轴向变形模态,而轴承的径向刚度主要影响进给系统的弯曲变形模态,且试验结果与计算结果基本一致,本模型能较好地表征系统的动力学特性。
滚珠丝杠副系统;有限元;模态分析;动力学特性
0 引言
滚珠丝杠副因其定位精度好、刚度高、摩擦系数小等特点,被广泛应用于各种工业设备、精密仪器的进给机构,尤其在精密数控机床的直线驱动执行单元中应用较多[1]。我国制造业基础设施落后,制造加工工艺不够精良。滚珠丝杠副加工精度不高,转速上不去,直接制约了其所应用的机床等精密设备的性能,这就需要我们对滚珠丝杠副动力学性能有更深入的了解。模态特性分析可用来确定结构的各阶固有频率和振型特点,是进行瞬态动力学和谐响应等分析的基础。
目前关于滚珠丝杠副系统动力学特性的有限元分析还比较少[2-4],且仅限于对丝杠模态及将滚珠简化后对进给系统的某一位置进行谐响应分析,未对螺母位置、支撑方式、工作台及两端支撑轴承对滚珠丝杠副系统模态特性的影响进行系统研究,且很少经过试验验证有限元计算结果的准确性。而螺母位置、工作台及两端支撑均对滚珠丝杠副系统模态特性有直接影响。因此,本文针对滚珠丝杠副结构特点,装配完整系统模型,探讨了螺母位置、支撑方式、工作台及两端支撑轴承对滚珠丝杠副系统模态特性的影响,并进行试验验证。
1 滚珠丝杠副系统简述
实际工况中螺母位置、支撑的方式、所连接的工作台及两端支撑轴承的刚度对系统模态特性都有着影响。本文选用某公司DK5025型滚珠丝杠副(主要参数如表1所示)为研究对象,设计工作台,并在丝杠副两端分别选用角接触球轴承(7006AC/P4)和深沟球轴承(6006/P5)作为支撑轴承。
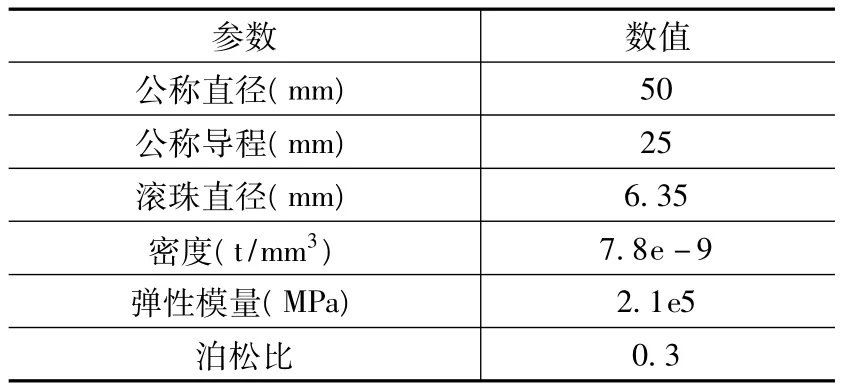
表1 DK5025型滚珠丝杠副主要参数
2 滚珠丝杠副系统模型的建立
2.1 滚珠丝杠副系统三维模型的建立
考虑到在有限元分析中小尺寸的键槽、倒角并不影响结构动态特性,故在建模时可将其忽略[5,6]。由于丝杠螺纹长度较长,导入有限元软件会引起大量失真,故仅在螺母所在位置附近画出螺纹。本文是在UG三维设计软件中建立滚珠丝杠副系统各部件的模型,并保存为*.igs格式。
2.2 滚珠丝杠副系统有限元模型的建立
将所建立的三维实体模型导入Abaqus有限元分析软件中。设置各部件材料属性为密度7.8e-9t/mm3,弹性模量2.1e5MPa,泊松比0.3。通过阵列平移等操作,将滚珠等部件按实际工况装配,滚珠丝杠副系统装配后如图1所示。对滚珠选用六面体,丝杠、螺母、工作台及轴承选用四面体和六面体进行网格划分,滚珠与滚道之间定义接触。
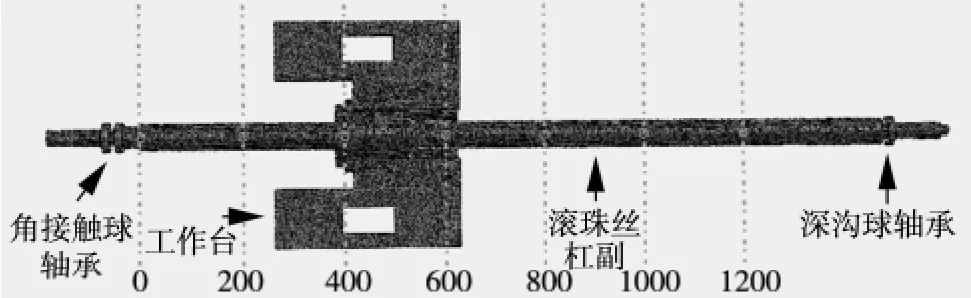
图1 滚珠丝杠副系统装配模型
对于结构特征值的计算,本文所选用的有限元分析软件Abaqus提供了子空间迭代法和Lanczos法。子空间迭代法求解较慢,但精度相对较高,而lanczos法采用稀疏矩阵求解器,求解较快并可提取大量的模态。本文选用lanczos法对结构模态进行求解。如图1所示,设丝杠左端始终为固定端,并定义丝杠螺纹柱面左侧端面为坐标原点,向右为坐标X正方向,依次将螺母法兰右端面置于X=0,200,400,600,800,1000,1200mm 处计算相关模态。
3 滚珠丝杠副系统的模态分析
3.1 不同支撑方式下,螺母位置对滚珠丝杠副模态的影响
滚珠丝杠副常用的支撑方式如表2所示。为了研究支撑方式对系统模态特性的影响,仅对滚珠丝杠副进行分析。

表2 滚珠丝杠副常用的支撑方式
螺母从左端移动到右端,如图2a所示,三种支撑方式下第一阶弯曲变形的固有频率均出现先增大再减小的趋势。“固定-支撑”的频率值略小于“固定-固定”的频率值,且在0mm至800mm段远大于“固定-自由”,在1000mm以后三种约束方式下频率值基本一致。由振型图(图3)可见,“固定-支撑”和“固定-固定”下,丝杠副第一阶弯曲变形的腹点位于螺母与两支撑端距离较长段的中点附近,即对于弯曲变形而言螺母和滚珠扮演了移动的弹性支撑的角色(如图4a所示)。“固自-自由”的自由端支撑刚度为0,故在0mm至800mm段其频率值远小于其他两种支撑方式。
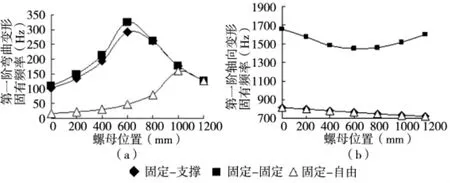
图2 支撑方式对第一阶弯曲变形(a)和第一阶轴向变形(b)固有频率的影响
如图2b所示,随着螺母的移动,“固定-支撑”和“固自-自由”第一阶轴向变形的固有频率出现减小的趋势,且变化趋势一致,而“固定-固定”则出现先减小再增大的趋势,且数值远远大于另外两种支撑方式。这是因为对于轴向变形而言,丝杠和滚珠扮演了沿轴向弹性支撑的角色。如图4b所示为丝杠副轴向振动简化模型。由材料力学可知,螺母左侧弹簧刚度随着螺母远离固定端而减小,对于“固定-支撑”和“固自-自由”,螺母右侧弹簧刚度为0,故螺母向右端移动时其第一阶轴向变形的固有频率出现减小的趋势。而“固定-固定”的螺母右侧弹簧刚度不为0,且随着螺母移动,右侧弹簧刚度出现增大的趋势,因而“固定-固定”的轴向刚度远大于其他两种支撑方式,其第一阶轴向变形的固有频率出现先减小再增大的趋势且数值远大于其他两种方式。
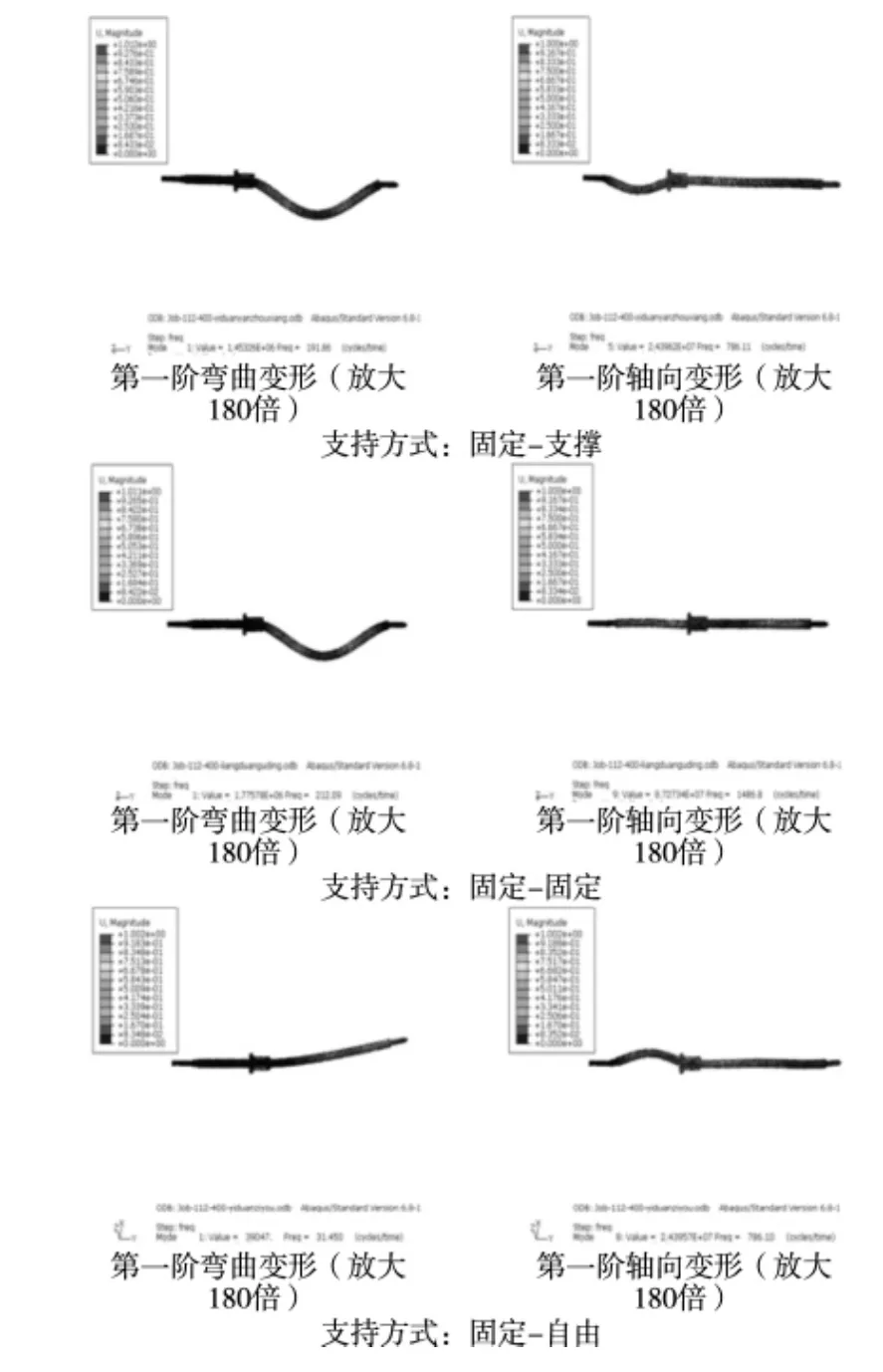
图3 三种支撑方式下,螺母处于400mm处第一阶弯曲变形(a)和第一阶轴向(b)变形的振型
由上述分析可知,螺母处于不同位置时,“固定-固定”的固有频率值最高,该方式可应用于高速、高精度的机床。相比较而言,“固定-支撑”的固有频率略小,但应用最为广泛,可应用于中速、高精度需求的机床。“固定-自由”的固有频率值远小于其他两种方式,其多应用于特殊需求的短丝杠且速度低、加工精度低的场合。
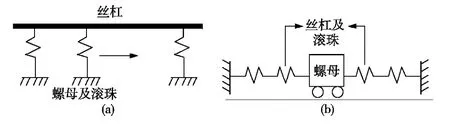
图4 丝杠副弯曲变形(a)及轴向变形(b)的简化模型
3.2 工作台对系统模态的影响
有限元计算中,在接触面参数未知,构件间通过多螺栓紧密连接的情况下,定义接触参数带来的误差远比忽略带来的误差大,因此可忽略进给结构接触面间滑移等变形,将接触面视为一个整体,不发生变形和脱离[7]。所以,本文在“固定-支撑”的支撑方式下,在工作台、螺母座和螺母之间的接触面使用“tie”定义约束,这样只考虑部件本身质量带来的形变影响。
在丝杠副上添加工作台后,随着螺母从固定端向支撑端运动,由图5可知,系统第一阶弯曲变形(振型特点如图6a所示)的固有频率基本不变,但第一阶轴向变形(振型特点如图6b所示)的固有频率迅速减小,减小的幅度逐渐增大。这是由于工作台的重力由两侧移动导轨支撑,并未改变图4a中螺母处的支撑刚度,仅相当于在图4b中增加了螺母的质量,因而系统的第一阶弯曲变形的固有频率基本不变,而第一阶轴向变形的固有频率值迅速减小。所以,在工作台设计中为了增大轴向振动的固有频率,避免共振的发生,应在满足工况需求的同时尽量减小工作台的质量。

图5 工作台对第一阶弯曲变形(a)和第一阶轴向变形(b)固有频率的影响
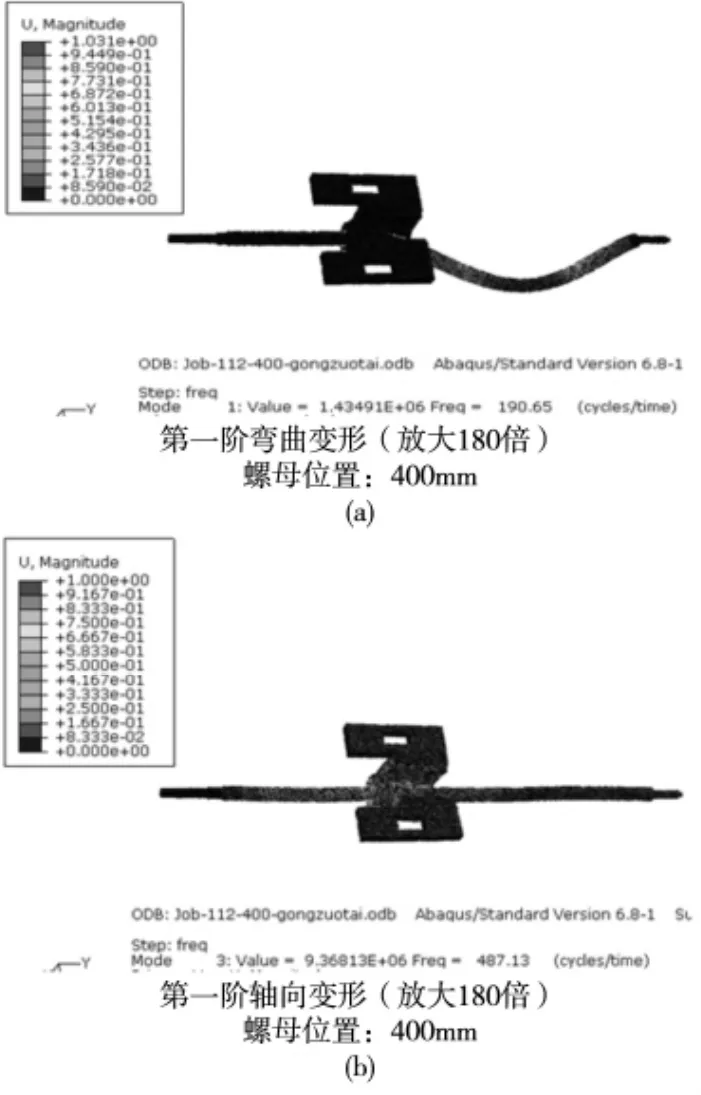
图6 工作台影响下,螺母处于400mm处第一阶弯曲变形(a)和第一阶轴向变形(b)的振型
3.3 两端支撑轴承对系统模态的影响
3.3.1 刚性联接
将丝杠两端与大地的固接替换为轴承支撑后,如图7所示,当螺母处于不同位置时,系统的第一阶弯曲变形和第一阶轴向变形的固有频率均减少(振型特点如图8所示)。
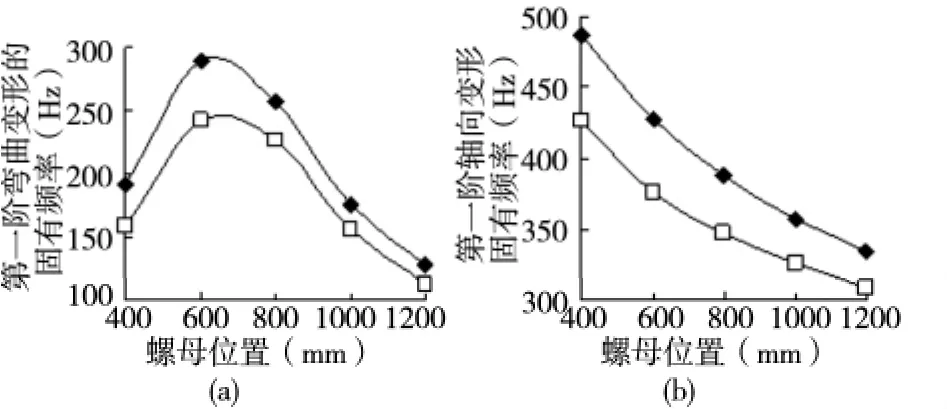
图7 轴承支撑刚性联接下第一阶弯曲变形(a)和第一阶轴向变形(b)的固有频率
由于实际装配情况,螺母仅能从400mm移动至1200mm处,因此刚、柔性联接下的计算仅从400mm处开始。替换为轴承支撑后,图4a、b两图中两端支撑的轴向和径向刚度值减小,因而其轴向和径向变形的固有频率值均减小。因此在进给结构的设计中为了增加系统的固有频率,避免共振,应尽量使用轴向和径向刚度较大的轴承或者增加轴承的预紧力,从而提高系统的稳定性。

图8 轴承支撑刚性联接下,螺母处于400mm处第一阶弯曲变形(a)和第一阶轴向变形(b)的振型
3.3.2 柔性联接
丝杠与两端支撑轴承之间的结合面特性对有限元分析结果的影响很大。本系统选用的是双列背靠背角接触球轴承(7006AC/P4)和深沟球轴承(6006/P5),通过查阅相关文献及厂家提供的技术参数可知:角接触球承轴向刚度为6.55e4N/mm,低预紧载荷为40N;深沟球轴承径向刚度为2.26e4N/mm。双列预紧角接触球轴承支撑刚度的经验公式[8]:
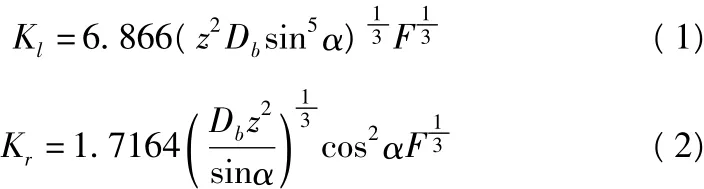
由(1)(2)可计算得角接触轴承径向刚度为:7.53e4N/mm。
将两端支撑轴承分别用径向和轴向与上述刚度数值相对应的弹簧代替。如图9所示,与刚性联接相比,柔性联接下,螺母处于不同位置时,系统的第一阶弯曲变形和第一阶轴向变形的固有频率均出现减少,其中轴向变形的固有频率变化较大。柔性联接下第一阶轴向变形的固有频率虽逐渐减小,但变化幅度较小(振型如图10所示)。可知当轴向支撑刚度减小到一定程度时,滚珠与滚道的接触刚度及丝杠的轴向刚度可忽略,可将系统的轴向振动等效为一个带有弹簧的质量块,仅考虑系统的质量。
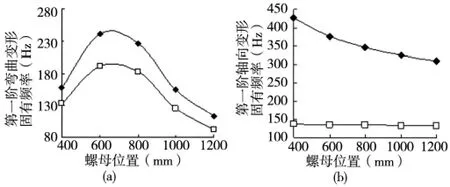
图9 轴承支撑柔性联下第一阶弯曲变形(a)和第一阶轴向变形(b)的固有频率

图 10 轴承支撑柔性联接下,螺母处于400mm处第一阶弯曲变形(a)和第一阶轴向变形(b)的振型
4 试验模态及结果分析
根据被测滚珠丝杠副系统的结构特点及试验现场的实际情况,本试验选择锤击法进行激振,通过固定传感器并移动力锤逐次敲击获得结构的频响函数。本试验选用德国M+P公司提供的便携式移动实时动态分析模块—SO Analyzer,模态试验所选用的分析设备如表3所示。

表3 模态试验分析设备
由于工作台安装的限制,仅能分别对丝杠上表面进行径向激振和对工作台进行轴向激振。在丝杠上表面沿轴向等间距(100mm)布置12个激励点,在连有工作台的螺母左右两侧面布置21个激励点。弯曲变形的测试点选在丝杠较长段上,离螺母距离为较长段1/4处,轴向变形的测试点为工作台左上角。
当螺母处于不同位置时对其第一阶弯曲变形和第一阶轴向变形的固有频率及振型进行识别。图11为螺母处于1200mm位置处,系统在X,Z(轴、径)向上的频响及模态指示函数曲线。经识别,1200mm位置处第一阶弯曲变形和第一阶轴向变形的振型如图12所示。表4和表5为螺母处于不同位置时,第一阶弯曲变形和第一阶轴向变形的试验值与有限元计算值的对比。可见,第一阶弯曲变形的误差较大,最高误差为7.05%,第一阶轴向变形的误差较小。计算结果与试验结果较吻合,能比较好的表征系统的动力学特性。
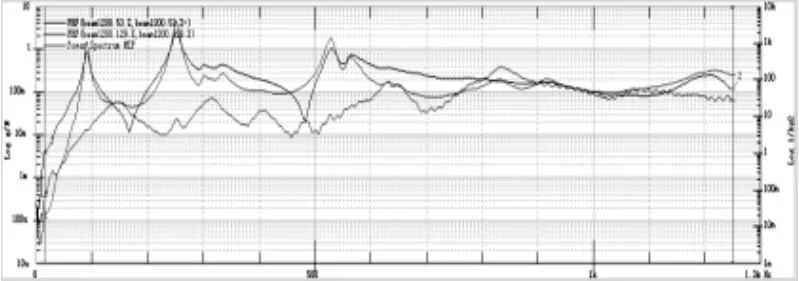
图11 螺母处于1200mm位置时X,Z向频响及模态指示函数曲线

图12 螺母处于1200mm位置时第一阶弯曲变形(a)和第一阶轴向变形(b)的振型图
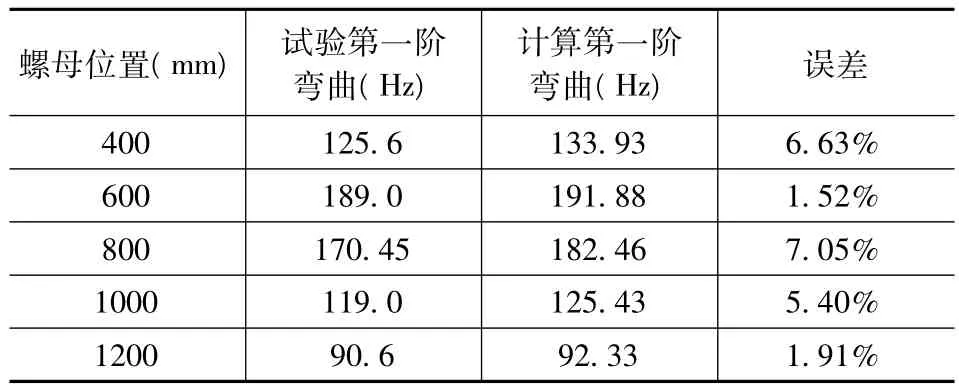
表4 不同螺母位置处第一阶弯曲变形的试验值与计算值对比

表5 不同螺母位置处第一阶轴向变形的试验值与计算值对比
5 结束语
在模态计算中,对于滚珠丝杠副系统的弯曲变形可将螺母及滚珠视为移动的径向弹性支撑,而对于轴向变形可将丝杠及滚珠视为轴向的弹性支撑。不同的需求场合需选择不同的支撑方式。滚珠丝杠副系统设计中为了避免共振的产生,提高系统的稳定性,在满足工况需求的前提下,可通过减小工作台质量以及增加两端支撑的轴向刚度来提高系统轴向变形的固有频率。同时,增加两端支撑的径向刚度可提高系统弯曲变形的固有频率。试验结果与分析结果基本一致,表明本模型能较好地表征系统的动力学特性。为设计者在设计研发时改变系统固有频率,避免共振,以及校核分析中提供参考信息。
[1]黄祖尧.精密高速滚珠丝杠副的最新发展及其应用[J].China Academic Journal Electronic Publishing House,2003,(4):36-40.
[2]宁怀明,王彦红.THK滚珠丝杠基于ANSYS的动态分析[J].煤炭技术,2010,29(7):18 -19.
[3]孟勃敏,吕玉清,任工昌.滚珠丝杠副共振可靠性的有限元分析[J].组合机床与自动化加工技术,2011:10-13.
[4]侯秉铎,许瑛,彭浪草,等.超精密滚珠丝杠副进给系统谐响应的有限元分析[J].组合机床与自动化加工技术,2011:20-22.
[5]李松波,马星国,韩辉.发动机曲轴的模态分析[J].沈阳工业学院学报,2003,22(4):72 -74.
[6]岳东鹏,孙奇涵,张伯俊,等.曲轴系统动态特性的有限元分析[J].天津工程师范学院学报,2006(1):4-8.
[7]陈爱民,菜英,张明.微驱动进给结构设计与模态分析[J].先进设计与先进制造技术,2009:23-25.
[8]李为明,王海涛.轴向定位预紧轴承刚度计算[J].河北工业大学学报,2001,20(4):15-19.
(编辑 赵蓉)
Analysis of the Anti-resonance of Ball Screw System
LIU Li,TANGWen-cheng,CHEN Yong-jiang
(School of Mechanical Engineering,Southeast University,Nanjing 211189,China)
In order to improve the stability of high speed ball screw system,avoiding resonance,modal analysis of the ball screw system is done using the FEA method.Discuss the influence of the positions of the nut,the strutways,worktable and the supporting bearing on the system mode.Finally,modal testing of the ball screw system is done w ith hammering method.The result shows that the choice of different strutways should depend on the needs of occasions.And both the quality of the worktable and the axial stiffness of the support have themain factor that affects the axial deformation mode of the system,and themain factor that affects the flexural deformation mode is the radial stiffness of the support.And the test results are consistentw ith the calculated results,thismodel can well characterize the dynamic characteristics of the system.
ball screw system;finite element;model analysis;dynamic characteristic
TH16;TG65
A
1001-2265(2012)08-0018-05
2012-04-17;
2012-05-15
国家科技重大专项项目(数控机床专项)(2009 ZX04011-031)
刘立(1987—),男,江苏人,东南大学硕士研究生,研究方向为先进制造技术等,(E-mail)615186849@qq.com。

