低压电力线载波通信组网的研究

吕玄兵 王 翥 王 玲

(哈尔滨工业大学(威海)信息科学与工程学院，山东 威海 264209)

低压电力线载波通信组网的研究

吕玄兵 王 翥 王 玲

(哈尔滨工业大学(威海)信息科学与工程学院，山东 威海 264209)

为改善目前低压电力线载波通信在实际应用中通信距离短、通信效果差的现状，给出了一种动态组网方法。首先通过网络初始化过程获取终端之间的通信质量;然后以通信质量为依据，分别采用Dijstra和粒子群算法两种优化算法选取中继节点，获取集中器与通信终端之间的最佳通信路径，并对这两种算法进行对比分析;最后对该组网方法进行了实际测试。测试结果证实该组网方法是可行的，改善了系统的通信效果。

电力线载波 动态组网 Dijstra 粒子群 中继节点 通信质量

0 引言

由于低压电力线载波通信利用已有的电力线作为传输媒介，无需另建通信线路，所以其应用非常广泛。但电力线信道不是用于通信的专用信道，载波信号传输时受电网情况的影响导致通信终端之间的通信距离和通信质量不稳定。单从物理层的研究来改善通信质量不仅难度大而且代价高，因此，国内有人在低压电力线载波通信系统中设置固定的中继节点来扩大通信范围，提高通信质量［1］。这种方法在一定程度上改善了通信效果，但由于受电力线信道情况的影响，通信终端之间的通信质量带有一定的时变性，所以设置固定的中继节点不能真正满足实际的要求。本文采用动态组网的方法，根据终端之间的通信质量动态选择中继节点，提高了系统的通信效果。

1 低压电力线通信组网背景

目前，低压电力线载波通信系统的构成如图1所示。集中器既能与分布在三相电力线上的通信终端通过低压电力线进行通信，又能与上位机通过串口、GPRS或者以太网等方式进行通信，低压电力线载波通信终端与集中器通过低压电力线进行通信，同时通信终端之间也能够通过低压电力线进行点对点通信。在目前的应用中，如远程路灯控制、自动抄表等，跨相通信的可能性不大，所以系统的物理结构决定了系统的网络结构应该是一个有三个分支的星型网络，每一个分支对应一相电力线上的通信终端，系统的组网可以看成是对三个分支上的通信终端分别进行组网。为适应动态组网的要求，每个通信终端分配一个唯一的ID号。

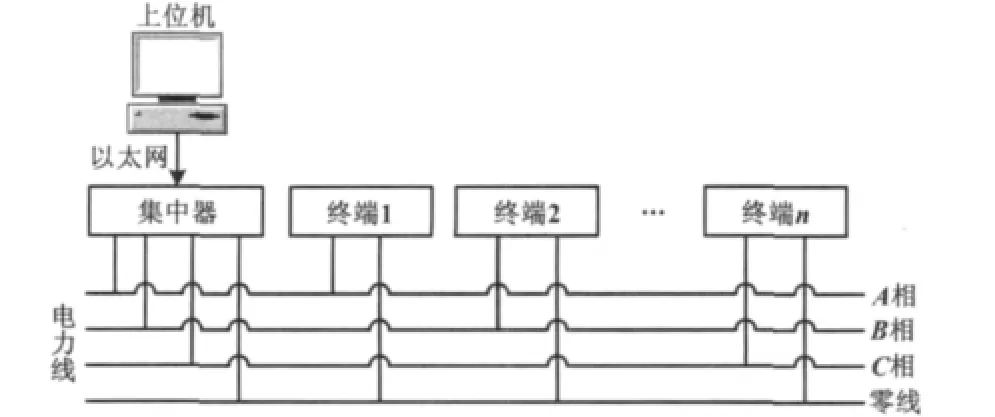
图1 低压电力线载波通信系统Fig.1 The low voltage power line carrier communication system

2 动态组网过程

动态组网就是系统本身能够根据终端通信质量动态地对网络进行重构和优化。方案整体上分为以下两个步骤。

①网络的初始化，系统刚开始工作时，所有的终端对于控制中心来说都是盲点［2］，控制中心需通过集中器对各个终端进行搜索和测试来获取终端之间的通信质量，建立一个网络信息表。

②组网过程，在已知网络信息表的基础上，通过某种算法获取集中器到各个通信终端之间的最佳通信路径，上位机通过集中器向下发送指令时，将中继节点的ID号包含在指令中，经过转发即可准确传输到目标终端。

2.1 网络初始化

在实际应用中，集中器与PC机之间的通信比较稳定，但很多通信终端不能直接通过集中器与上位机进行通信。所以上位机要通过集中器对所有的通信终端逐个搜索，并测试终端之间的通信质量。

假设上位机通过集中器进行第一次搜索时只搜索到A1、A2、A3三个通信终端，上位机会在搜索过程中测试出集中器与A1、A2、A3之间的通信质量。同理，当上位机通过A1、A2、A3发起第二次搜索过程时，会测试出A1、A2、A3这三个通信终端与其他通信终端之间的通信质量。

为避免信道的冲突，在搜索和测试过程中要根据终端的ID号依次进行一定的延时。实际应用中通信终端接收以及反馈数据的时间间隔很短，通信质量基本上不发生变化，所以认为终端的上行通信和下行通信的通信质量是一样的。

假设整个系统中有(N-1)个通信终端，加上集中器，上位机可以建立一个(N×N)的矩阵Q，Q(i，j)表示终端i与终端j之间的通信质量。

Q 定义为［3］:

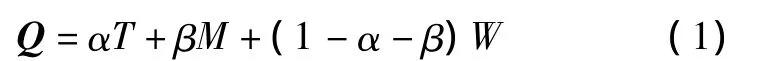
式中:T为通信时间，T的大小可以通过终端收发指令的时间间隔确定;W为误码率，W的大小通过对同一组数据收发来判定;M为负载数量，初始化过程中M的大小无法判断，M的初始值统一为1;α、β为两个参数，在不同的应用环境下(如通信终端数的不同、电网环境的不同)设定不同的值，用于调整通信时间、误码率和负载数量对通信质量的影响程度。

获取Q值后，为了减少系统的运算量，根据Q值的大小将通信质量划分为6个等级，即g={1，2，3，4，5，6}，g( i，j)表示终端 i与终端 j之间的通信质量等级。由Q的定义可知，Q值越大通信质量越差，通信质量等级越低，即g=1时通信质量最好。初始化过程结束后，可以得到元素为g( i，j)的矩阵G(N×N)，将G定义为网络信息表。

2.2 Dijstra算法的应用研究

Dijstra算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径［4］。将集中器视为定点S，需要进行通信的节点为N，假设S与N通信需经过的中继节点为:

利用Dijstra算法时，将其衡量标准变为终端之间通信等级之和为D，D( i，j)表示节点i和节点j之间通信时分支路径的通信质量等级之和，则集中器与终端N之间的最优通信路径即为:

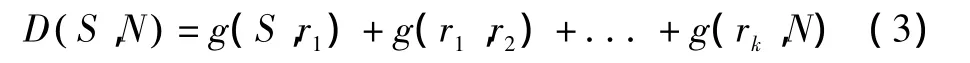
集中器与终端N之间的最佳路径即D( S，N)取最小值时的路径。

Dijstra算法流程如下［5］。

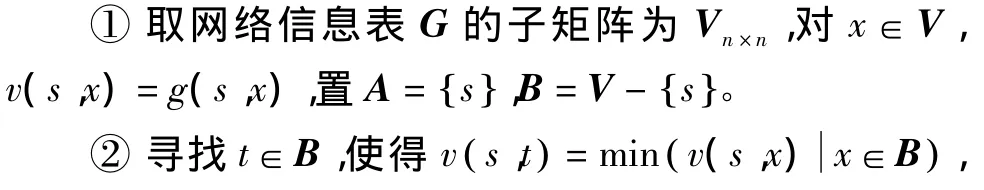
则v( s，t)就是t到s的最佳通信路径。

③ 令 A=A∪{t}，B=B-{t}。

④ 若B=φ，算法结束，否则转步骤⑤。

⑤ 对与 t相邻接的所有节点 x，如果 v(s，x)≤v( s，t)+v( t，x)直接转步骤②;否则令 v( s，x)=v( s，t)+v( t，x)，转步骤②。

由于仿真时无法实时反映电力线信道变化对通信终端的影响，因此取两个实际终端进行测试。根据测试结果，可以认为它们之间的通信质量在不同距离、一定范围内变化，如表1所示。

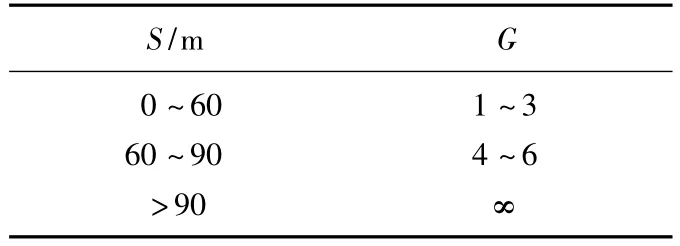
表1 通信质量的设定Tab.1 Communication quality settings

仿真时运用Matlab软件。设有41个通信终端，对其按N1～N41进行编号，集中器为N0。随意分布节点位置，仿真时得到的集中器N0与终端N41通信时的最佳路径如图2所示。

图2中的各个圆圈表示各个通信节点。由图2可以看出，N5、N14、N27、N36为求得的 N0与 N41之间通信路径的中继节点。

根据得到的网络信息表分析，在该路径中，D( N0，N )

41的值最小，即通信效果最好。

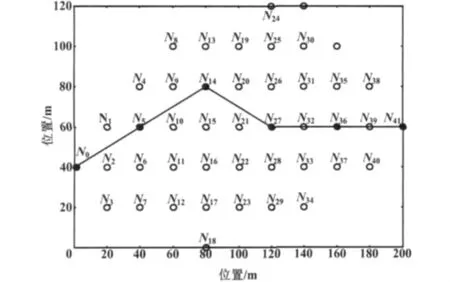
图2 集中器N0与终端N41之间的优化路径Fig.2 The optimal path between N0and N41

2.3 粒子群算法的应用研究

Dijstra算法逐次对比的运算思想往往使其得到的结果是最优的，其缺点是运算量比较大。因此，本文对粒子群算法也进行了研究。在与Dijstra算法相同的条件下，对粒子群算法进行仿真，得到对通信终端N41的寻优结果如图3所示。

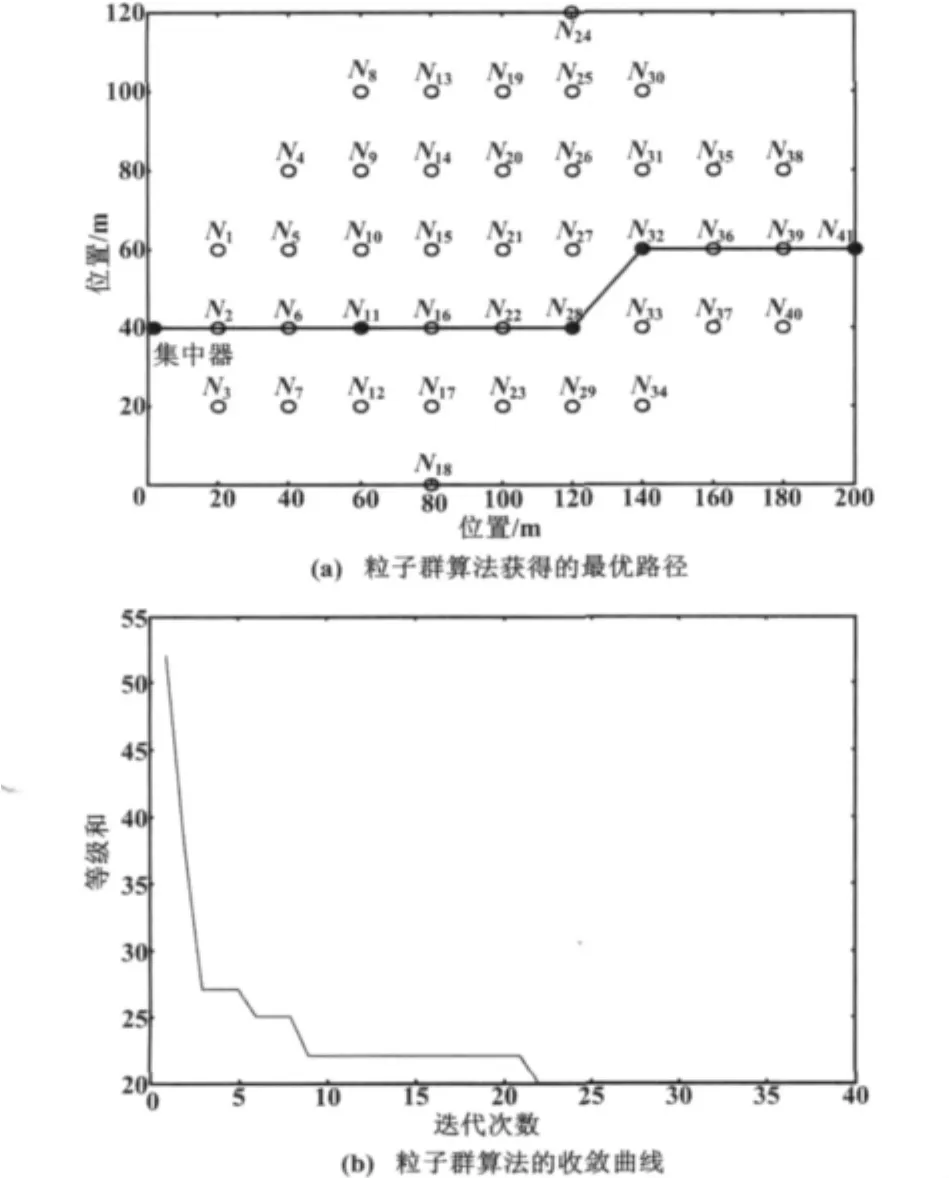
图3 寻优结果及运行收敛曲线Fig.3 The optimal result and running convergence curves

粒子群算法是一种群体智能优化算法。它将每个优化问题的解视为一个有位置和速度但没有质量的粒子。粒子在运动过程中记录自己的飞行历史最优值以及群体历史最优值，并结合这两个值对自身的速度和位置进行更新，反复迭代得到一个优化解［6］。粒子群算法运行流程如下:

①粒子初始化，首先赋予每个粒子一个随机解;②粒子自身进行更新;

③粒子个体分别与其个体历史最优值和其群体历史最优值进行交换更新［7］;

④判断是否达到最大迭代次数或求得的结果是否满足要求，若是则结束，否则返回步骤②。

应用粒子群算法时，可以将集中器与目的通信终端之间的通信路径看成一个离散序列，序列由集中器、中继终端、目的终端的ID号按顺序组成。

集中器与每个通信终端之间有很多条通信路径，即有很多离散序列，将每一个序列看成是一个粒子，即每个粒子对应一个解。

粒子在运动过程中将其对应的解与其个体历史最优值和群体历史最优值对应的解进行对比，根据差距的大小与个体历史最优值和群体历史最优值交换中继节点［8］。

2.4 两种算法的对比

在实际应用中，不仅要考虑到通信质量的问题，还要对组网时间进行考虑。本文研究了两种算法，在同样的条件下对它们的运行时间和通信质量进行仿真对比。

以通信终端N41为例，仿真对比图如图4所示。

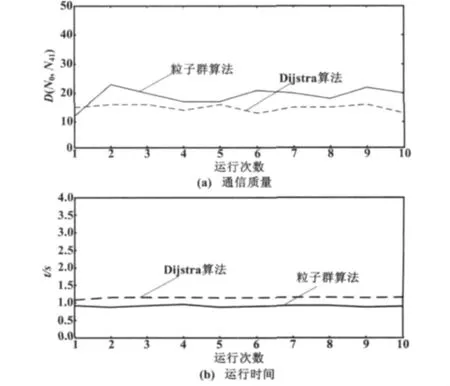
图4 两种算法的对比曲线Fig.4 The comparison curves of two algorithms

由图4可知，采用Dijstra算法进行寻优时通信质量较好，但是其运行时间明显比粒子群算法要长。所以在实际应用中，当系统中通信终端的数量较少时，可以选择Dijstra算法，但在通信终端数量较多且对通信的实时性要求较高时，可以采用粒子群算法。

3 组网方法的实际测试

为了验证文中提出的组网方法的可行性，本文选用实际通信终端进行了测试。

3.1 负载均衡性的研究

在实际应用中，由于通信终端所处的位置不同，靠近集中器的一些终端的通信质量可能一直比较稳定，致使系统运行时这些终端作为中继节点的次数明显偏多。由于电力线通信是单信道传输，若某一终端作为中继的次数过多，会导致通信延时较长并影响终端使用寿命［9］。

为使中继节点不过于集中在某些终端，在系统运行中对作为中继的终端进行记录，从而对通信质量Q中的系数β进行合理的调整。

3.2 系统的测试

实际的测试系统如图5所示。图5(a)为所有终端距离集中器30 m范围内测试时上位机生成的网络拓扑图，图5(b)为所有的终端分布在距离集中器70 m范围内的测试结果。

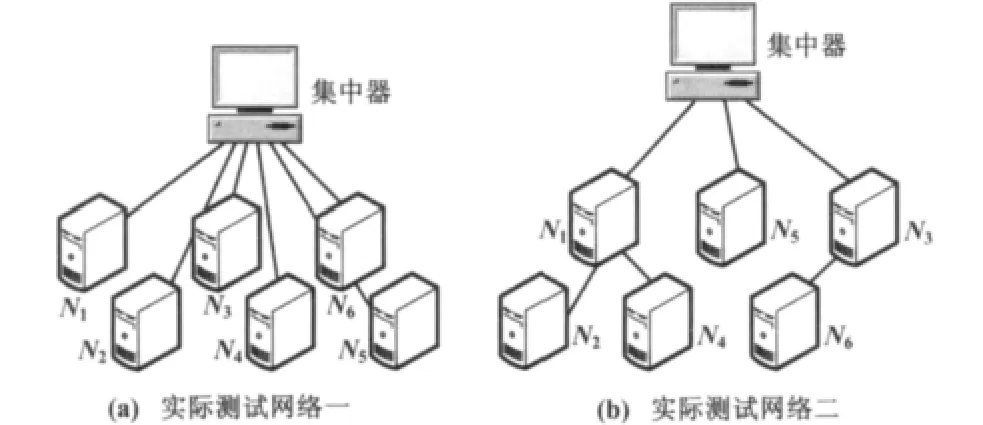
图5 实际测试网络Fig.5 The practical test network

集中器是系统的通信枢纽，每个通信终端能够按照上位机的指令测试其与其他通信终端之间进行通信时的通信质量。组网方法主要由上位机完成。上位机通过网络初始化建立网络信息表之后，将其转化为等级矩阵G，进而采用优化算法获取优化通信路径。上位机采用VC软件编写，其运行流程整体如下［10］。

①初始化集中器，开始搜索和测试通信终端。

②若搜索到所有终端，则进入步骤③;否则反馈有问题的终端，然后进入步骤③。

③等待用户指令，若收到通信指令，根据建立的网络信息表，利用寻优算法寻找最佳通信路径。

④判断获取的中继节点是否存在超载情况，若超载，则调整参数重新生成G;否则按此路径进行通信。

⑤发出通信指令后等待反馈，若收到反馈则结束;否则返回步骤②重新组网。

由于终端数量只有6个，因此采用Dijstra算法较为合适。测试过程中通过改变通信终端的分布范围来体现组网方法的动态优化功能。

由图5所示两个网络结构拓扑图可以看出，随着通信终端之间通信质量的变化，系统能够改变集中器与通信终端之间的通信路径，以获取更好的通信效果。

根据70 m范围通信时生成的通信终端之间的通信质量等级计算证实，图5(b)所示的集中器与终端N2、N4、N6之间的通信路径效果最好。这也证明了本文给出的组网方法是可行的，很好地改善了系统的通信效果。

4 结束语

本文给出了一种低压电力线载波通信系统动态组网的方案，分析了网络初始化过程，对网络寻优过程中采用的优化算法进行了仿真对比。测试结果证实该方法很好地改善了系统的通信效果，对提高目前低压电力线载波系统的通信质量以及扩大系统的通信范围具有重要意义。

［1］刘柱，汪晓岩，蔡世龙.低压电力线载波通信组网方法［J］.电力系统通信，2009，30(206):17-20.

［2］ Qi Jiajin，Liu Xiaosheng，Wu Di，et al.Study on power line communication routing method for low-voltage distribution［J］.Chinese Journal of Electronic Devices，2008，31(3):1303-1308.

［3］戚佳金，徐殿国，周岩，等.低压电力线载波通信网络特性模型与组网算法［J］.中国电机工程学报，2009，29(16):59-62.

［4］安红岩，胡光岷，何永富.网络最短路径的动态算法［J］.计算机工程与应用，2003，39(1):173-175.

［5］管志忠，刘永明.图论中最短路问题的MATLAB程序实现［J］.安庆师范学院学报，2007，13(1):26-29.

［6］黄少荣.粒子群优化算法综述［J］.计算机工程与设计，2009，30(8):1977-1980.

［7］黄岚，王康平，周春光，等.粒子群优化算法求解旅行商问题［J］.吉林大学学报，2003，41(4):477-480.

［8］孙湘，周大伟，张希望.惯性权重粒子群算法模型收敛性分析及参数选择［J］.计算机工程与设计，2010，31(18):4068-4071.

［9］ Zhao Lei，Zhu Hongsong，Xu Yongjun，et al.A load balanced and energy-efficient geographic routing for lossy W-SN［C］∥2007 International Conference on Intelligent Sensors，Sensor Networks and Information Processing，2007:119-124.

［10］Wang Zhenchao，Zhang Ye，Zhao Yuqian.A distributed routing algorithm for L-PLC network［C］∥ Proceedings of the IEEE International Conference on Automation and Logistics，Qingdao，2008.

Study on the Carrier Communication Networking for Low Voltage Power Lines

At present，the practical application of low voltage power line carrier communication only offers short communication distance and poor communication quality，to improve such condition;the dynamic networking method is proposed.With this method，firstly，the communication quality between terminals is obtained through the initialization process of network;then according to the communication quality，the Dijstra algorithm and the particle swarm optimization algorithm are separately used to select the relay nodes and get the optimal communication path between concentrator and communication terminal.Two of the optimization methods are analyzed and compared，and finally this networking method is tested practically.The test result verifies that the networking method proposed is feasible and improves the communication effect of the system.

Power line carrier Dynamic networking Dijstra Particle swarm Relay node Communication quality

TN913+.6

A

修改稿收到日期:2011-05-06。

吕玄兵(1987-)，男，现为哈尔滨工业大学(威海)控制科学与工程专业在读硕士研究生;主要从事低压电力线载波通信的研究。