基于PID神经网络的研究和改进

卢 萍 金朝永

(广东工业大学应用数学学院，广东 广州 510520)

基于PID神经网络的研究和改进

卢 萍 金朝永

(广东工业大学应用数学学院，广东 广州 510520)

针对PID神经元网络(PIDNN)将静态神经元扩充到动态神经元的特性，通过分析PIDNN控制算法存在的局限性，对变量系统的激励函数提出了改进方案，扩大了PID神经网络控制的适用范围。Matlab仿真测试表明，改进后的PIDNN系统具有良好的稳态性，试验验证了算法的有效性。

PID控制 神经网络 激励函数 误差 仿真

0 引言

随着控制理论和技术的不断发展，各类控制方法不断涌现。由于PID控制器具有结构简单、鲁棒性强、易于实现等优点，在很多方面都有广泛的应用。对具有不确定性和非线性的被控对象，传统的PID控制往往得不到满意的结果。为克服传统控制方法和一般神经元网络的缺点，将神经网络与传统的PID控制相结合，提出一种本质性的动态网络——PID神经元网络［1］。该方法利用梯度下降法使误差函数达到最小，存在收敛速度慢和易陷入局部极小这两个问题，在很大程度上具有一定的局限性。本文针对该情况，对多变量系统即单输出PIDNN(single-output PID neural network，SPIDNN)的激励函数进行修正，改进了算法。

1 SPIDNN的网络结构和算法

SPIDNN采用的是三层网络结构，其基本形式为2×3×1的结构，如图1所示。

图1中，SPIDNN网络共有六个神经元，包括输入层、隐含层和输出层三层。每个输入层有两个神经元，一个神经元接收目标值和给定值，另一个接收被控变量值。输入层神经元的输出经过连接权值，进入隐含层进行综合处理。隐含层的三个神经元为比例元、积分元和微分元，分别对输入信号进行比例、积分和微分运算。隐含层的输出再通过连接权值，进入输出层。输入层的神经元采用比例神经元，它完成整个网络控制规律的综合和输出。SPIDNN可以完成单变量的单输入-单输出系统的控制任务［2］。

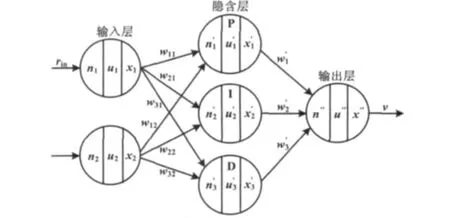
图1 SPIDNN的结构图Fig.1 The structure of SPIDNN

SPIDNN网络采用误差反向传播算法的神经元网络，从运行过程中的信息流来看，SPIDNN属于前馈型神经网络。该网络仅通过许多具有简单处理能力的神经元的复合作用使网络具有复杂的非线性映射能力，且没有反馈。SPIDNN的算法由前向算法和误差反传算法两个部分组成。

1.1 SPIDNN的误差前向算法

SPIDNN的前向算法根据网络的两个输入值，按网络当前权重值以及各层状态函数和输出函数形成网络的输出。

1.1.1 输入层

在任意采样时刻k，将输入系统被调量的给定值r(k)和实际值y(k)分别赋值给输入层的输入v，输出层神经元的状态u等于v，通过阈值函数确定输入层的输出x'i。

1.1.2 隐含层

隐含层是神经元网络中影响最大的层次。它存在比例元、积分元和微分元三个神经元，各自的输入均值v'j为输入层至隐含层的加权总和，即:

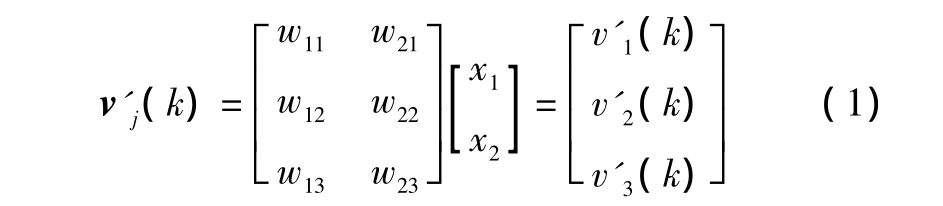
式中:wij(i=1，2;j=1，2，3)为输入层至隐含层的连接权值。它们的输入-输出函数分别为归一化的单位比例、积分和微分函数。比例元的状态函数为:

神经网络的比例元、积分元和微分元在隐含层与在输入层的输出方式都是通过阈值函数进行的。

1.1.3 输出层

神经元的输出为:

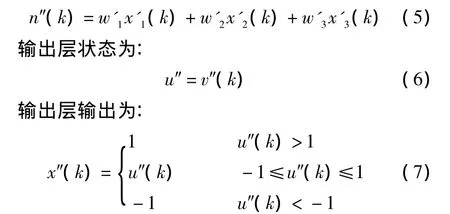
而SPIDNN的输出值与输出层神经元的输出值相同，即 v(k)=x″(k)。

1.2 SPIDNN的反向传播算法

根据梯度法调节SPIDNN的权重，按附加动量法

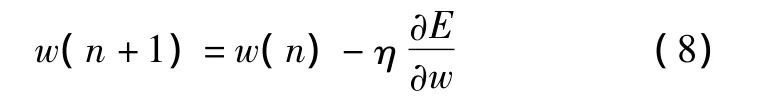
SPIDNN由前向算法和反向传播算法两部分组成，而反传算法的权值调节分别在隐含层至输出层、输入层至隐含层中进行。因此，下面将分别就隐含层至输出层、输入层至隐含层的反向传播算法进行说明。

1.2.1 隐含层至输出层

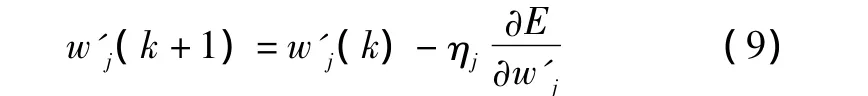
隐含层至输出层的权值迭代公式:调节网络权值，设学习步长为η，各层权值的迭代方程经过n步训练和学习后，各层权值的迭代方程为:

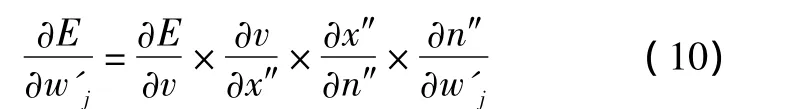
SPIDNN隐含层至输出层的连接权值算法修改为:

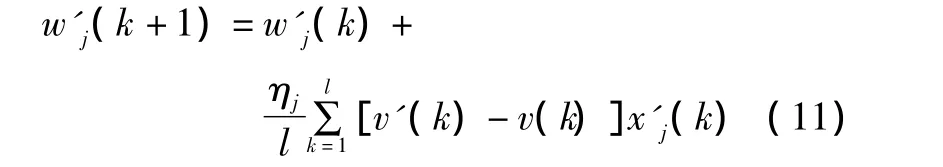
根据偏导数的链式法则，有:

式中:j=1，2，3。

1.2.2 输入层至隐含层

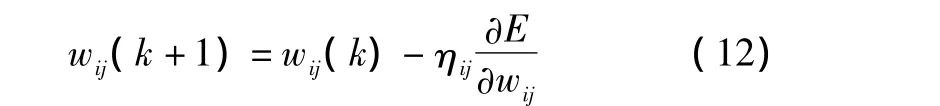
对式(12)的微分进行变形，可得:

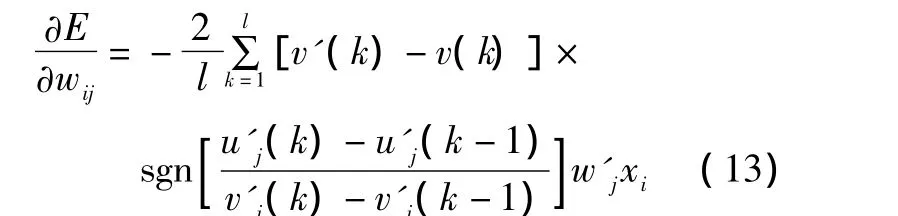
SPIDNN输入层至隐含层的连接权值算法修改为:

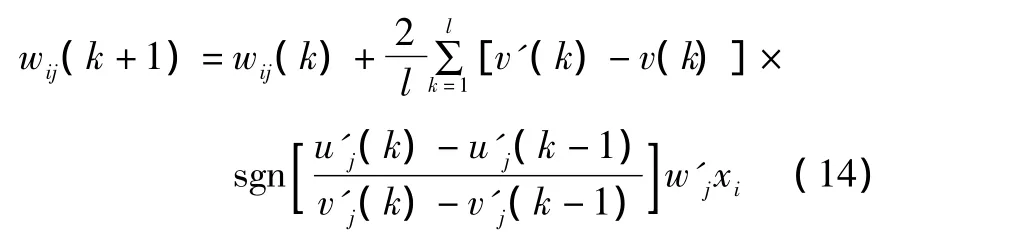
由SPIDNN控制系统的结构和算法可知，SPIDNN控制系统的算法不依赖于被控对象参数，而是根据控制效果进行在线自主学习，调整网络连接权值，实现对被控对象的控制。

2 SPIDNN的改进

SPIDNN存在无PID先验知识的控制系统，此时的初始权值只能随机取数;该网络的训练起点和收敛起始方向也都是随机的，陷入局部极小值的概率增大，容易使收敛速度变慢［3］。因此，对于无PID控制先验知识的系统初值必须加以改进。

2.1 激励函数对网络性能的影响

根据权值的迭代公式可知，在前提是保证收敛的情况下，权值的调整幅度越大，梯度的变化也相应变大，学习速度变快。由权值迭代公式可知，激励函数的导数与权值变化成正比例关系，同时，激励函数频繁使用，对整个网络的学习都起着重要的影响作用。

理论上，任意阶导数不为常数的函数都可以作为激励函数，当函数的导数趋于0时，输出值和期望值就很接近。因此，选用S型函数是比较合理的。若输出值和期望值相差较大，则有必要对算法进行一定的修正，否则函数将误差信号反传下去的难度增大，会导致误差函数的下降速度变慢，甚至还会出现误差函数不能下降的情况。此时，网络进入假饱和状态［4］。在饱和区中，激励函数的导数值很小，所以在每次学习中只能对权值作很小的修正，输出单元在一段时间内会在平坦区(局部极小值点或者是在鞍点)工作，使网络的均方根误差保持不变或变化很小。

2.2 激励函数的改进分析

激励函数在一定意义上可以决定误差函数的性质特征。任意阶导数不为常数的函数都可作为激励函数。但研究发现，很多常用的函数使网络陷入局部极小值的可能性较大，这无疑是需要改进的。

对于一般的神经网络算法，通常选用Sigmoid函数。大致的原因有两个:一是它与生物神经元的反应非常相似;二是导数比较简单。通常SPIDNN输出部分的激励函数是以阈值函数作为激励函数，也有以双曲正切函数tanh(x)作为激励函数的［5］，但这两种函数都有一定的缺陷性。阈值函数如下:

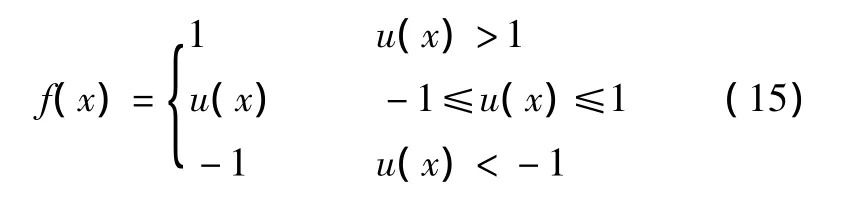
阈值函数将被控对象的输出限制在［-1，1］，当状态u(k)连续几次都大于1(或者都小于-1)时，输出v均为1(或者为-1)，反传算法中的权值2］(k)≈2］(k-1)。此时，易造成网络收敛速度减慢，甚至引起运算停止。双曲正切函数形式如下:

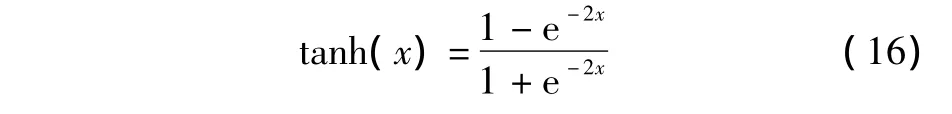
基于上述分析，应选择合适的激励函数并进行一些必要的参数调整。如果在网络的学习中，考虑误差的均衡性，使激励函数的导函数值可以随误差的变化而作相应的调整，可有效地避免麻痹现象的产生，加快网络的收敛速度［6-7］。

2.3 激励函数的改进

根据文献［7］，在原有的函数的基础上，对λx进行修正，并对激励函数进行改进［8］。具体调整如下:

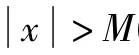
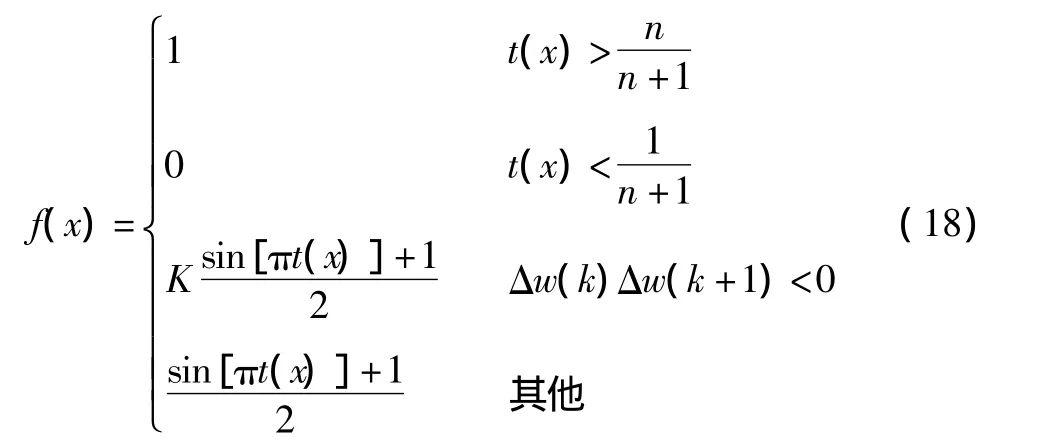
2.4 激励函数的进一步改进

对于上述改进的激励函数，数据的输入输出被限定在某个固定的范围内，基于初始权值的选取是任意的，激励函数对网络的影响也是不定的。为了更直接地避免落入饱和区，可对输入输出的参数进行数据的归一化［9］，避免激励函数陷入饱和区间上。

通过函数变化t(x)=0.8f(x)+0.1，将区间归一化为［0.1，0.9］。改进的激励函数可定义如下:

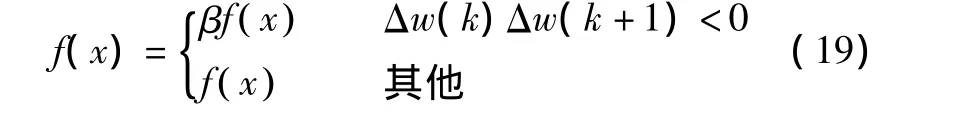
3 改进后的控制仿真效果

设被控对象的数学模型为:

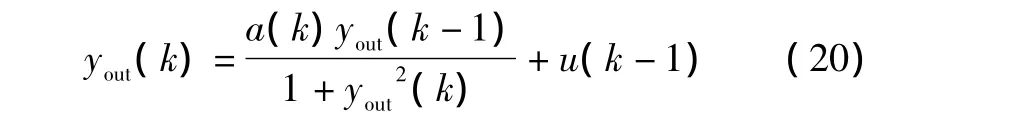
式中:系数 a(k)是慢时变的，a(k)=1.2(1-0.8e-0.1k)。输入指令信号(期望输出值为rin(k)=1.0)，初始步长η=0.05，动量因子∂=0.2，初始权值选区间上的随机数，采样周期ts=0.001 s［10］，用Matlab进行程序仿真，结果如图2～图4所示［11-12］。

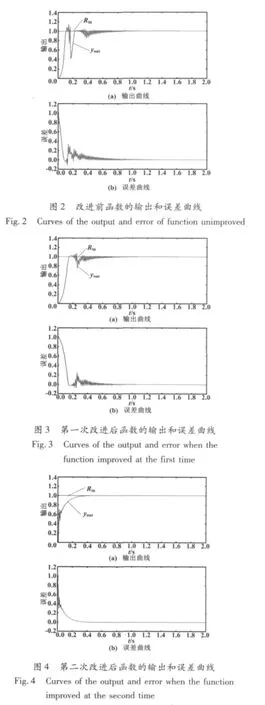
图2为在无PID先验知识时系统的输出曲线和误差曲线，图3为根据式(18)改进后的SPIDNN学习得到的输出曲线和误差曲线，图4为根据进一步改进后的SPIDNN学习得到的输出曲线和误差曲线。对比图2～图4所示曲线可知，改进的SPIDNN控制系统在经过一段时间的学习之后，在较短时间内可以达到较好的性能［13-14］。

4 结束语

通过分析激励函数对网络性能的影响，对神经网络控制中的激励函数进行改进，使激励函数实现了动态性，扩大了系统控制的范围。同时，采用数据归一化处理，有效地消除或减少了区间变形误差的影响，降低了误差。但是，由于神经网络中存在许多不确定性，在实际的工程应用中应选择在符合实际情况的区间内对问题进行讨论。在同等条件下，采用文中的三种情况进行仿真试验，结果表明，改进后的SPIDNN控制系统得到了较好的收敛性，有推广应用的价值。

［1］舒怀林.PID神经元网络及其控制系统［M］.北京:国防工业出版社，2006.

［2］崔冉，王维庆，赵春平，等.基于PID神经网络的变桨控制系统的辨识［J］.仪器仪表用户，2008，15(6):74-75.

［3］翟尧杰，舒怀林，熊胜祖.PID神经网络改进研究［J］.机电工程技术，2010，39(8):39-41.

［4］孙娓娓，刘琼荪.BP神经网络的联合优化算法［J］.计算机工程与应用，2009，45(12):50-54.

［5］李文峰，刘军营，盛蕾.一种改进的基于神经网络模式的PID控制研究［J］.系统仿真技术，2007，3(4):217-220.

［6］肖俊芳，王耀青.一种激励函数可调的快速BP算法［J］.自动化技术与应用，2002，21(6):26-29.

［7］潘寿.BP神经网络模型中活化函数对网络性能的影响研究［J］.安徽师范大学学报:自然科学版，1998，2(3):218-221.

［8］陆琼瑜，童学锋.BP算法改进的研究［J］.计算机工程与设计，2007，28(3):648-650.

［9］胡伍生.神经网络理论及其工程应用［M］.北京:测绘出版社，2006.

［10］刘金琨.先进PID控制MATLAB仿真［M］.2版.北京:电子工业出版社，2006.

［11］宋滨，谷丽娜.基于神经网络的PID控制［J］.青岛大学学报:自然科学版，2001，6(3):90-91.

［12］王洪东，李丽，白金泉.MATLAB在控制工程中的应用［J］.控制工程，2003，10(3):273-275.

［13］陈玉银，吴刚.锅炉液位测量改进及PI参数整定［J］.石油化工自动化，2009，45(3):84-86.

［14］李明，杨成梧.PID神经网络的改进PSO学习算法［C］∥第25届中国控制会议论文集(中册)，黑龙江，哈尔滨，2006.

Research and Improvement Based on PID Neural Network

Due to PID neural network(PIDNN)possesses the characteristics of expanding static neuron to dynamic neuron，thus through analyzing the limitation of the PIDNN control algorithm，the improved strategy for the excitation function of variable parameters is proposed to extend the applicable range of PID neural network control.The Matlab simulation test shows that the improved PIDNN system possesses excellent stability;the effectiveness of the algorithm is verified through experiments.

PID control Neural network Excitation function Error Simulation

TP18

A

广东省自然科学基金资助项目(编号:S2011010005029)。

修改稿收到日期:2011-09-16。

卢萍(1986-)，女，现为广东工业大学应用数学专业在读硕士研究生;主要从事人工智能控制技术的研究。

行业信息