基于仿真的物料平衡系统测评

张 睿 陈 瞭 荣 冈 冯毅萍

(工业控制技术国家重点实验室、浙江大学智能系统与控制研究所，浙江 杭州 310027)

基于仿真的物料平衡系统测评

张 睿 陈 瞭 荣 冈 冯毅萍

(工业控制技术国家重点实验室、浙江大学智能系统与控制研究所，浙江 杭州 310027)

为了更好地测评石化企业生产执行系统(MES)软件的物料平衡模块数据校正功能，提出了一种基于仿真的数据校正结果的测评方法。该方法通过搭建仿真模型产生全厂物流过程的真值，并应用动态数据驱动方法进行模型参数的修正，即通过向仿真真值添加测量误差生成误差可配置的测量值，模拟现场真实的测量网络;应用物料平衡系统及其内嵌数据协调算法对测量值进行数据校正得到校正值，将校正值分别与仿真真值、测量值进行对比，定量评估数据协调算法的性能。相对于仅比较校正值和测量值的原评定方法，该方法能更加精确、全面地测评数据校正算法的效果，并在某石化企业的案例中得到验证。

生产执行系统(MES) 物料平衡 数据校正 测评与改进 仿真模型

0 引言

生产执行系统(manufacturing execution system，MES)通过控制包括物料、设备、人员、流程指令和设施在内的所有工厂资源来提高制造竞争力，确保整个生产行为的最优［1］。MES的核心在于准确地跟踪物流并及时、快速处理生产管理中的问题［2］，为生产执行系统中的其他模块或企业内其他应用系统提供精确的数据支撑。数据校正是MES软件应用的重要技术之一，通过综合集成物流数据，实现对生产信息、储运信息和质量信息的汇总和管理。通过应用数据校正软件，实现过失误差检测与数据协调计算，保证物流数据的准确性、完整性和一致性，进而支持生产统计、生产调度和生产计划等各种应用［3］。

自20世纪60年代开始研究的数据校正技术，能较好地处理过程数据的缺失和误差，降低变量随机误差的影响，剔除人为或者仪表故障引起的显著误差。但成熟的数据校正理论算法在工厂的实际应用中效果并不理想，尤其是在面对大规模全厂级问题时。这是因为生产实际的测量数据很难符合某种既定概率分布，变量协方差的获得变得十分困难;同时规模过大的矩阵延长了求解时间，有些时变的过程连接模型更是加大了求解的难度。

为解决生产实际中的物料平衡问题，MES除了应用传统数据校正算法，还普遍采取由物流平衡计算和不确定量推理规则共同组成的数据校正新算法。在针对MES层物料平衡问题中，以物流平衡计算和不确定量推理为主，传统数据校正技术为辅。相应的软件主要有Honeywell的Business.FLEX PKSTM，ASPEN Tech的 Plantelligence，Emerson、Siemens、Schneider 的 MES方案，中国石化的SMES等。

对于这类物料平衡模块的平衡结果，企业普遍采用如下指标来评价:①平衡推量有解;②单变量协调率小于设定比率;③全厂平衡内部收益率(inner rate of return，IRR)指标;④节点残差率(损失率);⑤进出厂量与库存变化的差量。

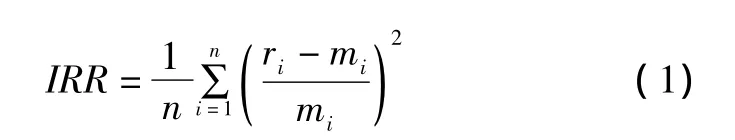
式中:n为节点个数;mi为变量的测量值;ri为平衡结果。一般认为，IRR指标越小越好，即整体协调量变化不大。这种思想接近于传统数据校正的最小二乘。但仔细分析可见，IRR指标并不能完整地反映平衡效果，如假设某变量测量值带有显著误差，该变量的平衡结果偏离真值而接近于测量值，IRR指标相应缩小，给人平衡结果良好的错觉;而且IRR指标很容易忽略由于系统缺陷而没有检测到的显著误差。

这种新数据校正技术的结果是否正确，是否足够接近真实值，从工程化的应用软件方面来说，无法准确定量测评。要从根本上测评结果，就需要把平衡后的数据与生产数据真值作比较，而不仅仅依靠人的经验或者平衡结果与测量结果的距离去判断。唯有用真值进行比对，才能知道平衡的结果是否接近真实。但不论采用何种高等级、高精度的仪表，测量数据总会带有误差，也就无法获得生产真值。

仿真技术是过程系统工程中一门重要的技术。仿真技术在流程行业的引入，大大提升了工业设计、制造和培训的水平。依据一定的方程关系，仿真技术对输入或者全局变量进行验证计算，得到真值输出。真值的获得，对工艺模拟、物料平衡测评至关重要。针对MES层全厂物料平衡的测评问题，本文提出在测评环节引入仿真技术，在待测评的数据校正软件外搭建特定的符合MES测评需要的平行仿真模型(仿真计算严格满足测评需要模型的各变量真值)，再对平行计算出的真值进行相应误差化，以测试物料平衡系统对于测量数据的平衡性能。将平衡结果与仿真真值进行比对，构建基于真值的测评指标，可以定量分析平衡效果，是测评物料平衡系统工业应用的有效辅助手段。比利时学者Radermecker对CAPE-OPEN标准下的应用校正软件进行过测试［4］，但国内仍无学者对工厂级数据工程软件进行过基于仿真的全面测评。

1 待测评物料平衡系统介绍

本文测评对象为某真实石化MES物料平衡系统。该系统工作流如图1所示。系统基于网络测量层的仪表读数和生产操作层物料移动操作，建立以班为周期的物料移动操作记录，通过班移动操作记录，形成一定周期内满足标准规范的物料移动事件或移动记录，并基于此进行显著误差侦破。之后，在准确解析物料移动模块物理节点量和物理移动关系的基础上，利用统一规则库、算法库、工厂模型和模型求解器，自动完成节点拓扑模型的动态生成和节点量平衡计算。最后，采用人机协同模式对物料进行再次修订，达到炼化企业的调度级平衡，为生产调度提供数据支撑。

图1 物料平衡系统工作流Fig.1 Workflow of material balance system

结合生产实际，测评所选择的物料平衡系统选用由物流平衡计算和不确定量推理规则共同组成的新数据校正算法，取代了传统的数据校正计算。不确定量推理规则包括进出厂和互供基准、储罐库存基准、单路优先基准、高准确度节点基准、收方基准和装置指标约束等。

2 仿真测评平台的设计与实现

生产过程数据的实际真值无法获得，使得数据平衡模块的测评停留在依据经验的模糊判断水平上，缺乏精确的理论依据。如何获得真值成为物料平衡系统测评的关键。应用准确的工厂仿真模型生成过程仿真值并取代真值是唯一有效的方法。仿真真值的应用可以对相应数据平衡模块的测评提供有力的支撑。因此，以测评为目的，本文开发了以仿真为基础的数据平衡软件测评平台。其原理为根据待测软件的模型搭建流程完全匹配的仿真模型，并对模型的匹配性进行验证。模型生成的仿真值即为真值，按照一定的规则给侧线上的真值加以随机误差与显著误差，通过实时数据库导入待测评物料平衡系统进行自动的物料平衡。最后，结合真值，通过提出新的评价指标对平衡结果进行评定和分析。物料平衡系统测评原理图如图2所示。另外，系统嵌入了传统数据校正算法模块，可将其输出与系统输出做进一步对比。

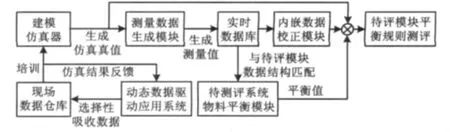
图2 物料平衡系统测评原理图Fig.2 Evaluating principle of material balance system

2.1 建模仿真器

流程工业基础信息建模包括生产流程建模和基础数据建模。Visio图形化建模拥有良好的开放性和兼容性，所以选用图形化建模方法进行生产流程的辅助建模［5］。模型属性自定义配置截图如图3所示。其中，虚线框内为乙烯装置配置的属性数据。

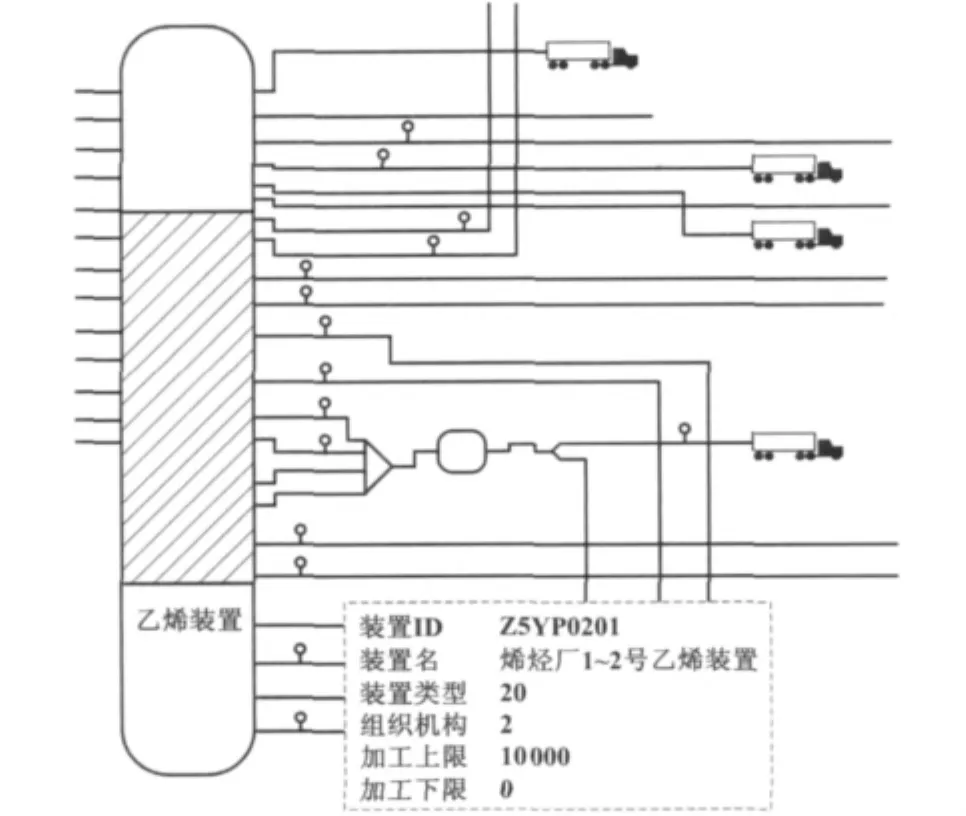
图3 模型属性自定义配置Fig.3 Self-defined configuration for model attributes

在图形化模型库中，每个基础设备模型按照功能需求都定义了完备的实体属性。此外，还通过开放数据库互连(open database connectivity，ODBC)与后台的关系数据库进行交互操作。对于移动关系的连接，本文利用Visio宏功能进行二次开发，建立FillMvmtProp函数，使得移动拖拽完成后，移动上下游节点信息进行自动填充，不需要人为补充。

传统的数据建模是基于导入的静态数据。然而随着传统仿真与测量技术的发展提高，传统的仿真模型利用输入早期测量的试验数据进行模拟，其仿真结果已经偏离实际系统的真实行为，不能对系统行为作出准确的分析与预测。因此，需要对仿真系统进行改进，加入反映实际系统真实行为的外来信息，增强模型的准确度。近年来应用工程科学领域出现的动态数据驱动应用系统(dynamic data driven application system，DDDAS)正是为解决这类问题而生［6］。DDDAS使用模型计算结果和外部数据的差距来控制仿真模型的修正以及外部数据的选取。

在基础数据模型的设计中，本文对I类变量和II类变量作了区分。I类变量指在工厂实际中的高精度量，一般不做调整，测量值可作为“真值”，应保证相关变量的仿真结果与实际严格相符。II类变量多为装置侧线，在生产实际中相应仪表精度较低或者数据缺失现象严重，但若建立的平行模型是准确的，则仿真真值结果经过数据协调后仍应与原仿真真值一致，否则模型必须作修改。结合生产实际及现场工程师的经验，本文提出如图4所示的仿真策略。

图4 仿真策略Fig.4 Simulation tactics

模型仿真的基本原理是已知上期罐存、进厂量、罐 付出、分流点系数、装置生产方案，求解移动、装置进、装置出、出厂量、罐收、当期罐存。该方法通用于大多数石化企业MES规模的仿真求解。

2.2 测量值生成

根据生产实际以及工厂核算基准，进出厂数据为法定经济核算数据，假设其不存在误差［7］。罐区有较高精度仪表，大部分为自动检尺，测量数据假设不存在随机误差，但少数人工检尺有可能引入显著误差。装置侧线的仪表精度较低，加之有可能出现的装置泄漏或仪表故障，存在大量随机或显著误差。依据以上原则，在测量值生成模块，对装置侧线仿真真值加入±5%以内的随机误差。

默认情况下，随机选取装置侧线变量数5%的侧线数，并加入20% ～30%的显著误差。根据案例设计，一般会生成仅含有随机误差、独立侧线变量带显著误差、关联侧线变量带显著误差三种不同测量值的情况对校正软件进行测评。

2.3 测评指标定义

由于没有明确的评判标准，全厂IRR指标数值的大小和趋势均不能反映系统校正效果的好坏。可见，唯有获得真值，将测量值、校正值与真值通过多种评价指标进行对比、分析，才能客观、准确地评判系统校正效果，并指导系统的改进。

本文定义如下指标［8］:

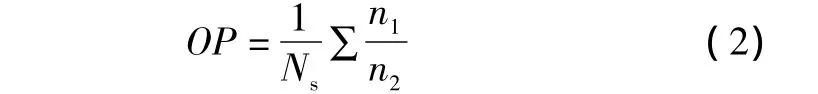
式中:Ns为仿真采样次数;n1为正确识别的显著误差数;n2为显著误差仿真数。OP值越大，表示系统检测显著误差的能力越强。

式中:Ns为仿真测试次数;n为节点数;ri，k为第i个变量第k次平衡结果;mi，k为第i个变量的仿真测量值;ti，k为该变量仿真真值。

IRR1描述了系统测量值偏离真值的平均程度，IRR1越大，则系统的输入测量值平均误差率越大。IRR2描述了系统平衡值偏离真值的平均程度，IRR2越大，则系统的平衡值平均误差率越大。RT更好地描述了系统修正测量误差的能力，RT值越小，系统去除误差的性能越好。

统计数据证明，当系统测量值误差率增大，带显著误差的变量比例增大时，随着系统识别、校正显著误差能力的下降，IRR值并没有持续上涨，所以不可以依据IRR值的变化判断物料平衡系统数据校正的效果。

3 案例分析

SMES(Sinopec-MES)是以MES集成平台为核心，上与企业资源计划(enterprise resource planning，ERP)层、下与生产操作优化控制层集成，提供统一的数据访问机制的、炼化一体的整体解决方案和应用系统。SMES采取的是“2+1”物料平衡方式，即首先在生产控制层，以装置为界区，利用装置投入产出历史数据，对装置侧线原始数据进行小范围的最小二乘的数据协调［9］。在此基础之上开展MES层和统计层数据平衡。

调度层的生产平衡策略以进出厂量、罐存变化量等高精度数据协调装置侧线数据，底层装置侧线协调原始结果作为调度层侧线差量分摊的比例数据参考依据。调度生产平衡的结果传入统计层。

统计层从物料的角度，对调度层协调结果的各侧线量按单物料进行全厂平衡，找出差异，指导精细化生产管理。调度层和统计层的平衡数据基础来源于装置层。这就消除了一个工厂存在多套模型而无法互用，每一层数据独立无法通信、无法协同平衡的问题。

相比于传统数据协调方法，在面对大规模问题时，不确定量推理规则能快速得到一组解，可行性和可操作性远优于传统协调方法。在现场，工程师会将SMES系统ERP层的月、旬统计值与工厂实际报表进行对照，以判断软件平衡的质量。这种判断虽然有一定的可靠性，但是失去了及时性，且不利于纠正系统的问题。

基于仿真的测评可以联合现场操作进行，提高了测评的及时性和有效性。测评结果有利于指导系统进一步修正数据校正算法。

选取SMES3.0中某烯烃厂2011年1季度运行数据搭建仿真案例。该厂一共有8套装置、37个罐、55个进出厂点、474条侧线、237条移动、69个分汇流点。Visio图形化建模辅助流程建模，通过提取1季度共90天物料日统计平衡数据，通过数据驱动的模型校正系统得到各装置的投入产出模型，产率模型考虑了装置的加工损失。

3.1 模型验证

首先验证仿真模型与SMES中烯烃厂模型的一致性。模型验证时校正值误差率分布图如图5所示。经过动态数据驱动系统的迭代修正，仿真结果带入待评系统得到的误差可以忽略不计，说明仿真模型与待评系统中的模型匹配，可以进行测评。

图5 校正值误差率分布图Fig.5 Distribution of corrected error rate

3.2 随机误差处理能力测评

将带有±2%以内随机误差的测量值带入SMES系统中，平衡后得到平衡值。平均误差率从3.717%下降到1.068%，测量值最大误差率为“3#丁二烯损失虚拟出厂”的62.658%，平衡后该项校正值误差率下降到25.712%，误差率显著下降，如图6所示。

图6 带2%随机误差校正值误差率分布图Fig.6 Distribution of corrected value error rate with 2%random error

将产生的50组、连续7个班次、侧线带±2%以内随机误差的仿真测量值，送入SMES生产平衡模块，7个班次IRR1均值为0.39，IRR2均值为0.21。侧线随机误差平衡结果如表1所示。

表1 随机误差平衡结果比较Tab.1 Comparison of random error balance results

以上结果显示，对于侧线仅存在随机误差的情况，SMES数据校正算法的作用不是非常明显。

3.3 独立侧线误差处理能力测评

本文将独立侧线定义为单入/单出节点(罐、装置或进出厂点)所对应的单独侧线。选取“1#丁二烯装置工业用丁二烯出”侧线添加35%显著误差，其他侧线添加±2%以内的随机误差，平衡后得到平衡值。测试结果显示平均误差率从8.988%下降到0.680%，设置的显著误差“1#丁二烯装置工业用丁二烯”测量值误差率为35%，平衡值误差率为0%，误差消除。具体误差率数据对比如图7所示。

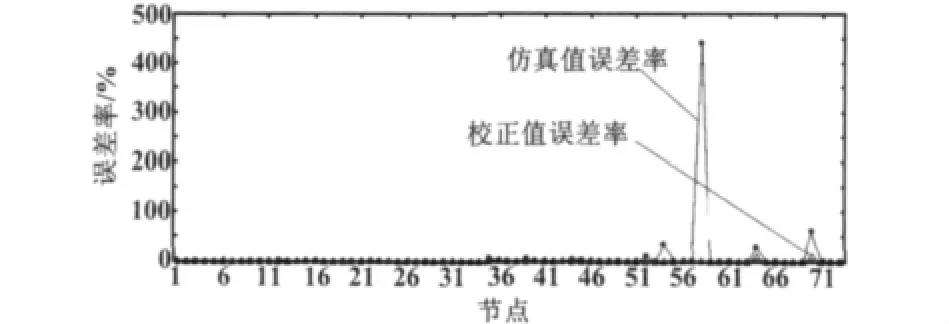
图7 带显著误差校正值误差率分布图Fig.7 Distribution of corrected error rate with significant error

3.4 关联侧线误差处理能力测评

在所有侧线变量上分别选取10%、15%、25%的变量个数，分别加入25%、35%、100%显著误差率进行测试。此时的侧线变量不再全部是独立侧线，随着显著误差变量数增多，关联侧线越来越多。

进行5×7=35组仿真试验(连续7班次，每班次5组数据)。试验结果如表2所示。

由表2可知，当显著误差率不变时，随着选取添加显著误差的变量数量的增加，OP值减小，说明显著误差的识别率降低;RT值趋势不明显，说明去除显著误差的能力变化无法判断，若要判断，需要具体分析选取显著误差侧线之间的关联关系。选取相同数量的侧线添加显著误差时，随着显著误差率的增大，OP值减小，显著误差的识别率降低，RT值增大，系统去除显著误差的能力减弱。

然而，采用式(1)所示IRR判断系统的校正能力，与本文提出的RT对比得到如图8所示的评价指标变化趋势图。

表2 试验结果Tab.2 Test results

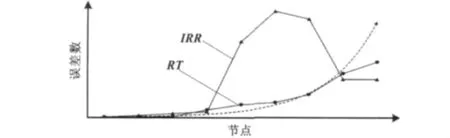
图8 评价指标变化趋势Fig.8 Trend of variation of evaluation index

由图8可以看出，随着显著误差数量的增加、显著误差率的增大，带显著误差的关联侧线数增加，系统排除显著误差的能力逐步下降，RT值始终可以正确地反映出系统的变化趋势，评价系统的校正效果;而IRR值在一定范围内可以正常反映系统的平衡效果，但误差数增加到一定程度后，指标便失效。可见，本文引入的RT指标显著改善了系统对平衡结果的判别。

4 结束语

本文结合模型管理技术、数据驱动模型修正技术，搭建了匹配待评系统中工厂模型的仿真模型。将仿真模型产生的真值及可配置的测量值自动推送到待评物料平衡系统中，并提出一套完善的评价方法，对平衡结果进行测评和分析。文章使用SMES系统中的烯烃厂模型作为测试案例，搭建仿真模型进行验证，并利用其生成的测量值对SMES物料平衡系统数据校正算法进行了测评。同时，分别选取侧线随机误差、单一侧线显著误差、关联侧线显著误差等误差分布形式，对待评软件进行全方位的测评，选取多种评价指标对结果进行分析。各项结果有效地辅助了生产平衡系统数据校正算法的改进。

［1］褚健，荣冈.流程工业综合自动化技术［M］.北京:机械工业出版社，2004.

［2］王化雨.数据校正技术及其在制造执行系统中的应用［D］.杭州:浙江大学，2010.

［3］郭超，金晓明，荣冈.数据校正技术在流程工业企业物料平衡中的应用［J］.化工自动化及仪表，2005，32(3):39-41.

［4］ Radermecker E，Dumont M N，Heyen G.Adaptation and testing of data reconciliation software for CAPE-OPEN compliance［J］.Computer Aided Chemical Engineering，2009(26):303-308.

［5］李笕列.流程企业模型与数据管理研究［D］.杭州:浙江大学，2009.

［6］ Darema F.Dynamic data driven applications systems:a new paradigm for application simulations and measurements［C］∥Computational Science-ICCS，2004:662-669.

［7］张路恒，张平福，董天翔，等.公路进出厂计量管理在石化企业MES深化应用中的进展［J］.自动化博览，2010(11):64-66.

［8］ Narasimhan S，Jordache C.Data reconciliation ＆ gross error detection:an intelligent use of process data［M］.Oxford，United Kingdom:Gulf Professional Publishing，2000.

［9］李德芳，蒋白桦，王宏安.石油化工行业生产执行系统应用研究［J］.天津大学学报:自然科学版，2007，40(3):335-341.

Evaluating Material Balance System Based on Simulation

In order to better evalute the results of data correction function of material balance module of MES software in petrochemical enterprises，the evaluation method based on simulation for data correction results is proposed.The true values of the material processes in the whole plant are generated through establishing simulation model，and the correction of model parameters is conducted by applying dynamic driving method.Specifically，through adding measurement error on simulation true value to generate measurement with configurable error，the on-site true measurement network is emulated，by using material balance system and its embedded data coordinate algorithm，the data correction is implemented to obtain corrected value.The corrected value and emulated true value，and measurement are respectively compared to evalute the performance of data coordinate algorithm quantitatively.This method is more accurate than original evaluating method;it evaluates the effects of data correction algorithm comprehensively，and is verified in cases of certain petrochemical enterprise.

Manufacturing execution system(MES)Material balance Data correction Evaluation and improvementSimulation model

TP273

A

国家973基金资助项目(编号:2012CB720500);

国家863基金资助项目(编号:2012AA041102)。

修改稿收到日期:2012-05-29。

张睿(1987-)，女，现为浙江大学控制理论与控制工程专业在读博士研究生;主要从事流程工业数据校正方面的研究。