相位物可视化的研究
肖中粲,潘永华,高惠滨
(南京大学物理学院,江苏南京210093)
1 引 言
光从物体中透射后会携带该物质性质的相关信息,所以分析出射光的各个参量对研究物质性质有很重要的意义.光所携带的信息主要是相位和振幅两部分,现有的所有感光器件包括人眼都只对光强发生反应,也就是振幅的模平方.如果是相位物体,由于其各处振幅透射率相同,光透射过后就只有相位部分变化,因此直接测量相位物透射光是不可行的,必须将相位信息转化为振幅信息,从而使相位物的像可视化[1-2].相位物样品的结构信息主要体现在折射率或厚度的不均匀[3],在生物科学、材料科学和凝聚态物理中广泛存在,如活细胞、一些晶体微粒和流体中的湍流等,所以相位物可视化有很重要的研究价值.
几种常见的相位物可视化方法包括暗场法、纹影法、相衬法和微分法.James Hooke首先演示过纹影法的作用,Toepler和Schardin推广了这一方法[4];荷兰格罗宁根大学的Frits Zernike于1935年提出相衬法,并于1941年发明了第一台相衬显微镜[1],1953年还因此获得Nobel物理学奖;1971年S.K.Yao和S.H.Lee则提出利用复合光栅在频谱面空间滤波实现微分运算[5],也实现了相位物可视化.
本文从理论、实验和数值模拟3个方面对4种常见相位物可视化方法进行了分析比较,得出了各种方法的优劣点和适用范围,提出了利用低频正弦光栅替代复合光栅滤波,用三重干涉实现效果上类似微分运算的图像处理方法,最终实现相位物可视化.
2 基本理论
在图1所示的凸透镜成像光路中,透镜对物光有傅里叶变换的作用[3]:
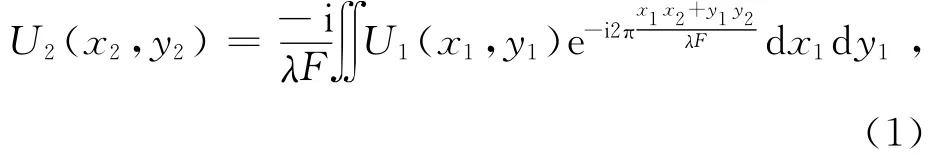
其中,U1(x1,y1)是物面光场函数,x1和y1是物面坐标;U2(x2,y2)是频谱面光场函数,x2和y2是频谱面坐标.
频谱面到像面是又一次傅里叶变换[3]:
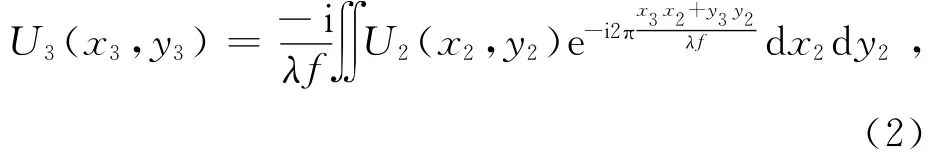
其中,U3(x3,y3)是像面光场函数,x3和y3是像面坐标.

图1 凸透镜成像示意图
现分别以f,g,h代表物光函数、频谱面光函数、像函数,则凸透镜成像光路中各平面的傅里叶变化关系可表示为为简化推导过程,可设光路放大系数为1,并忽略透镜的空间反射效果,即取
图1所示光路中,若物面上放置的相位物的屏函数是eiφ(x,y),入射光场为A(x,y)(在不影响讨论的情况下可视作常数A),则物光复振幅为f(x,y)=Aeiφ(x,y).对f做级数展开,可得,也就是[3]
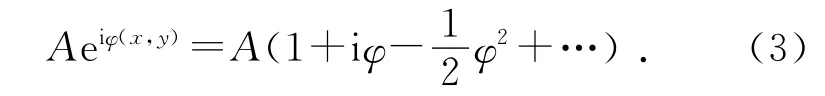
可以看出,光场级数展开的第一项是零频分量,对应背景光;第一项以后是相位频谱,对应由于相位变化而产生的衍射光.对于相位物,背景光和衍射光之间有π/2的相位差,它们相干叠加后,干涉为零,这就是背景光上观察不到衍射光,也即像面上看不到像的根本原因.那么,如果在频谱面上放置合适的滤波器进行适当滤波,改变背景光和衍射光之间的相位正交关系,则可以在像面上得到相位物的像.设滤波器的复振幅透过率函数为l,则傅里叶变换关系变为⊗f,其中⊗表示卷积.
1)相衬法
相衬法[1,3]采用的滤波方式是给零频分量附加上相位δ,使频谱分量变为…),则复振幅变为A(eiφ(x,y)+eiδ-1),光强变为I=|A|2(eiφ+eiδ-1)(eiφ+eiδ-1)*,即[3]
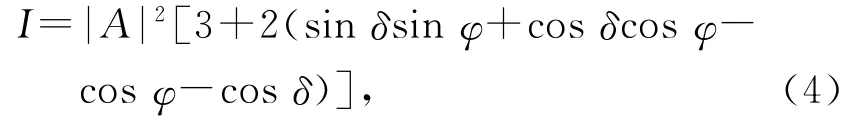
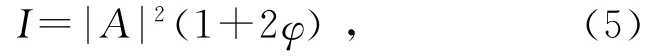
于是得到光强随相位线性变化的像.
2)暗场法
通过类似的分析方法,可知如果挡住零频分量,则复振幅变为A(eiφ(x,y)-1),由I=|A|2·(eiφ-1)(eiφ-1)*有:

当相位是小量时,

于是得到光强与相位平方呈线性关系的像.由于此时相位物的相位是小量,所以暗场法得到的像的亮度较小.
3)纹影法
纹影法的做法是挡住频谱面上一半的分量,例如y≤0分量.从傅里叶变换的角度讨论,h=^l⊗f,其中屏函数l(x,y)=H0(y)为Heaviside阶跃函数故[6]
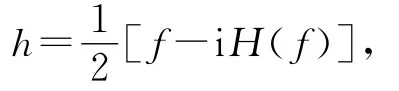
其中H表示Hilbert变换.于是,

像屏上得到的最终结果是物光场的Hilbert变换的函数.Hilbert变换在信号处理中作用依信号特点有不同侧重.不过在这个光学事例中可以从物理的角度理解,遮挡频谱一半内容后沿着该方向的相位函数上升沿信息被过滤,从而使相位物可视化.下面的实验和模拟都对这一观点给予了证实.
4)微分法
此方法核心思想是将光场的波前分成完全相同,但有(Δx,Δy)相对位移的两部分,并使之发生干涉,得到相位差分的函数f(x+Δx,y+Δy)+f(x,y),则I=2+2cos[φ(x,y)-φ(x+Δx,y+Δy)].取Δφ=φ(x,y)-φ(x+Δx,y+Δy),上式简化为

微分法对产生的像有边缘强化的作用,类似于浮雕的效果,能明显地观察到相位梯度大的边缘,但相位物内部相位没有梯度变化的部分仍不可见.
光路上微分法可由复合型正弦光栅滤波实现[3],设条纹沿x方向排列,则其屏函数为
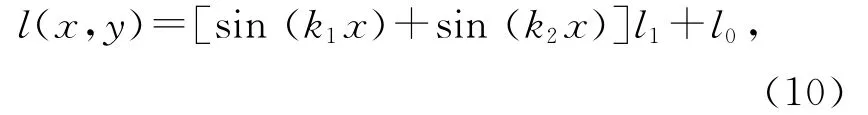
其中l1,l0分别代表透过率条纹周期的峰值和本底透过率.其频谱为最终成像结果是:
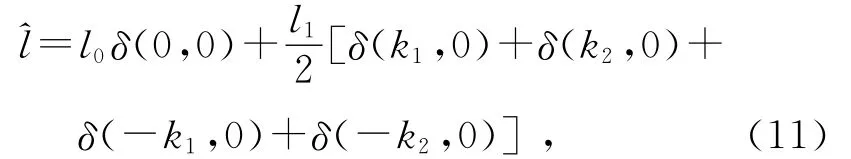
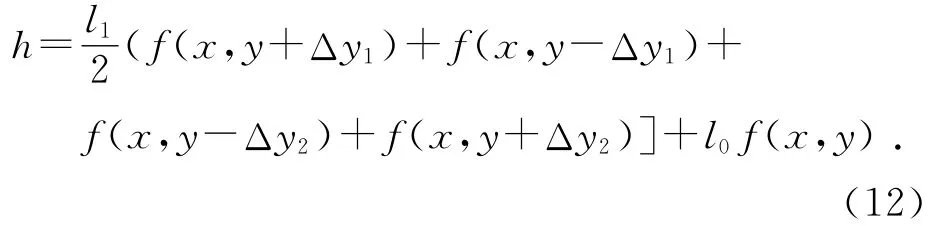
像面上的结果为,分别以复合正弦光栅的零级衍射点和2对1级衍射点为中心,共5组与原始图像完全相同像的叠加.如果使用高频复合光栅,k1和k2都较大且取值接近,可以使2个+1级衍射点和-1级衍射点与0级衍射点相隔较远但相互靠近,靠近的2个1级衍射点的像发生干涉,就可以分别产生2组图像微分的结果.
3 实验内容与初步分析
实验光路如图2所示,选取合适的透明相位物体成像,利用傅里叶透镜进行光学变换,在频谱面上用适当滤波器进行滤波,在像平面承接变换结果.
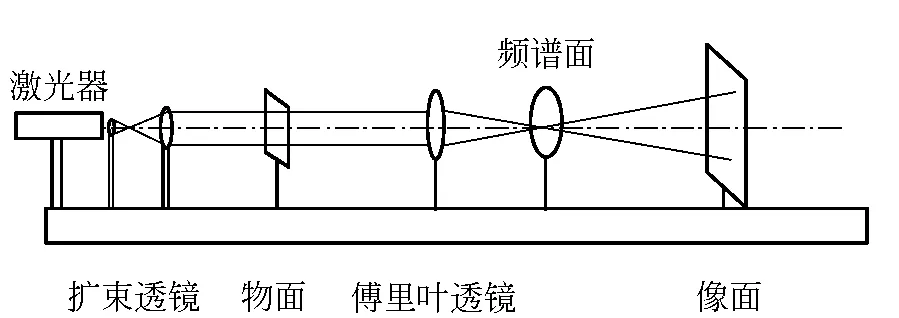
图2 实验光路图
3.1 滤波
实验中实现几种可视化方法所采用的滤波方案如下.
1)相衬法:以全息干版为底片,用留有小孔的黑纸遮盖曝光,时间控制在5~10s,之后进行显影20s,定影10min,水洗3h,将曝光处沉淀银粒洗净[7].最后以Mach-Zehnder干涉光路检查曝光点与非曝光处乳胶膜厚度差,选取产生相移最接近所用激光器半波长的点为滤波器[7-8].
2)暗场法:小圆屏滤波.
3)纹影法:架设刀片滤波.
4)微分法:全息照相法制作正弦光栅[9-10].由于实验条件所限,只制得了低频正弦光栅[11-13].由于低频正弦光栅屏函数为
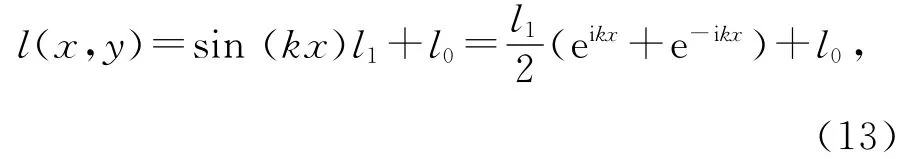
其频谱是很靠近的2个1级衍射点和1个零级衍射点,最终的成像结果是3组靠近的原始图像的叠加.它们之间发生三重干涉,显示出相位函数.
可以计算出此时像面上光强为
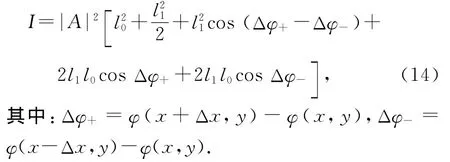
3.2 相位物
实验中选用了以下几种不同特点的物体,放置于物面上进行研究.
1)胶水涂敷的文字“FOX”.其特点是字型有所不同,且边缘处相移量迅速变化,缺点是产生相移较大且不均匀,而且随时间推移胶水干燥后透射率会下降.
2)超声光栅.利用超声波在水中传播形成驻波,引发密度周期性变化,进而引发折射率变化产生相移.这种相移是周期函数,而且由于密度变化小,它的相移量也小;但是由于驻波波长短,导致相移函数的条纹间距小,难观察.
3)液膜湍流.由于液膜边缘湍流导致的厚度和密度变化所致相移.其优点是各处透射率一致,是理想的相位物,缺点是作为相位物体,相位函数无法控制.
4)混合中的冷热水.是密度变化的相位物,相移小,缺点在于它是三维结构的物体,因此成像难以反映其完整内部信息.
3.3 实验结果及分析
图3~6是实验中采用的4种相位物成像的比较图.

图3 胶水文字成像图

图4 超声光栅成像图

图5 液膜湍流成像图
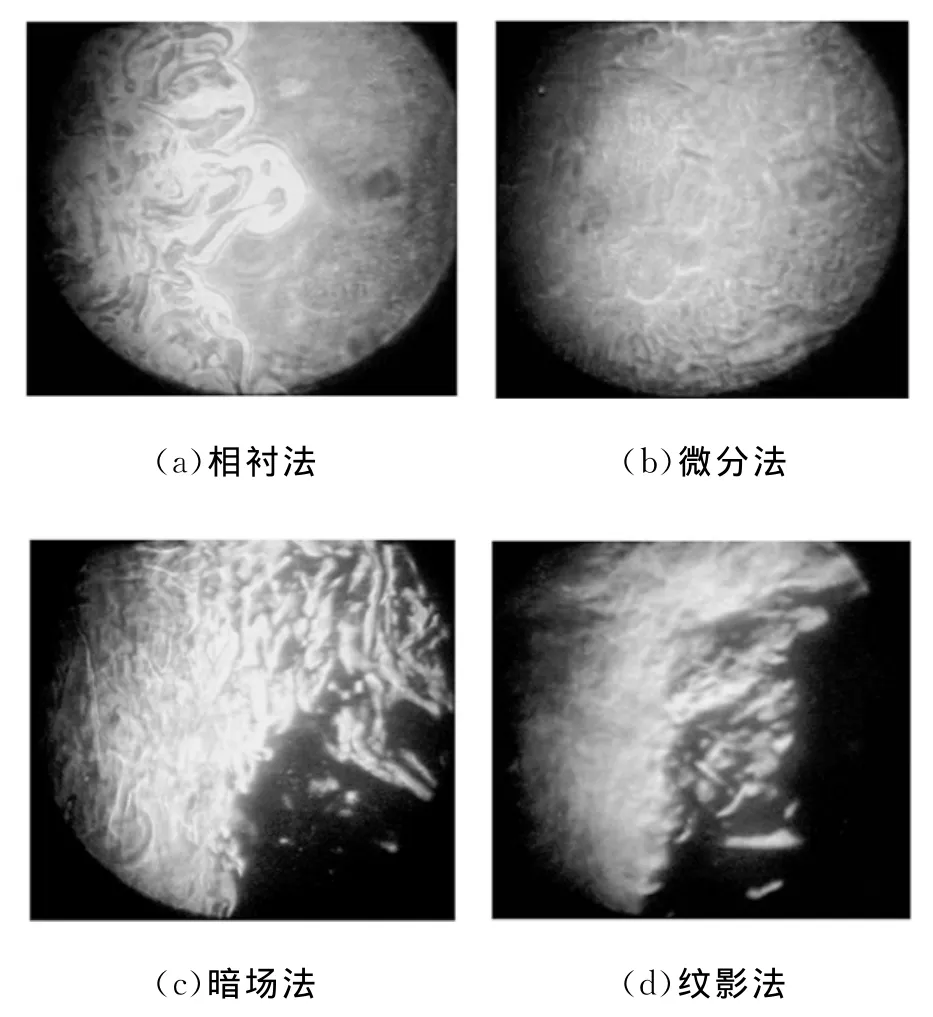
图6 冷热水的混合成像图
对实验中涉及的几种方法的初步分析如下:
1)相衬法
由式(4)可以看出,相衬法成像的亮度是相位的周期函数.在相位变化范围很大时,亮度会发生周期变化,产生条纹[胶水涂敷的文字非常平滑,而图3(a)中可以看到文字笔画内部有周期条纹].但是当条件控制合适时,使相位是小量,且相移接近π/2,有式(5),亮度基本与相位线性相关.成像效果较好,这些可以从图4(a)、图6(a)与其他方法的结果比较中看出.
2)暗场法
从式(6)可以得出,暗场法成像的亮度同样有周期性变化规律,这点在图3(c)中有所反映.然而对小相位物体成像,从式(7)看出亮度相位关系不成线性,而是二次方关系,因此不能准确反映相位信息.而且相比相衬法,暗场法对微小相位比大相位成像亮度低得多,不能很好地显示出微小的相位.从图5(c)与图5(a)及图6(c)与图6(a)的对比可以清楚地看出暗场法对一些细节显示的效果不如相衬法.
3)纹影法
纹影法成像规律由式(8)给出,其推导适用于刀片将零级频谱一起遮挡的情形.如果不遮挡零级频谱,由傅里叶变换性质,最终像面光场则变为h′=A+h,I′=|A|2+2Re(Ah)+I,可近似为
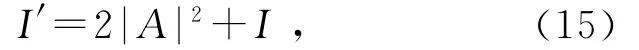
即不遮挡零级频谱相当于增加背景光强[3],会降低对比度.本次实验出于提高对比度的考虑,采用了遮挡零级频谱的方案,只有在超声光栅成像时由于亮度过低采取了不遮挡零级频谱的方法.从图4(d)、图5(d)与其他方法的对比可以看出,图5(d)的亮度很低,而图4的(d)对比度很低,所以在对微小相位的显示方面,纹影法是很难做到对比度和亮度同时提高的.
而从图3(d)、图6(d)可以看出,纹影法成像结果有立体感,这一点可以从Hilbert变换的性质解释.而从物理的角度解释,可以理解为遮挡一半频谱时将一个方向的相位上升沿信息排除了,只保留该方向下降沿,产生立体感.
4)微分法
实验中采用低频正弦光栅滤波的微分法成像,规律由式(14)确定.小相位时相位变化量也是小量,则
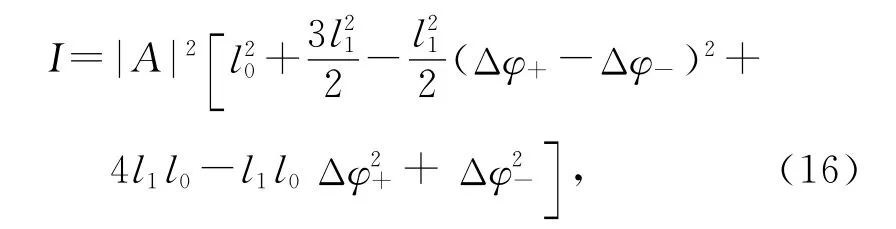
如果再考虑相位是缓变的,且l1<l0,则一项可以省略,则
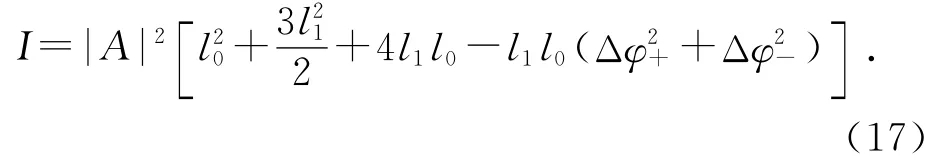
这样最终成像是相位函数2个方向相反的差分的平方和,同样可以起到边缘强化的效果.但是有对比度不高的缺点.这一点可以从图3~6的(b)中看出.
4 数值模拟
为了完善结果,弥补实验中的相位物缺陷,对实验中未能实现的方法进行研究,对几种相位物可视化方法进行了数值模拟.
1)模拟方法
对于实验中涉及到的相衬法、低频正弦光栅滤波的微分法、暗场法、纹影法,先用离散的矩阵f表示物光场,以傅里叶变换处理物矩阵f得到频谱g,再将g各元素与屏函数l元素一一相乘,最后再次用傅里叶变换处理得到矩阵h,求模后将其以位图形式画出.另外由于实验中没有制备出高频复合正弦光栅,没有完成微分法,所以模拟中添加了微分法,其实现方案是将矩阵f的元素平移数行数列后和原矩阵相加再直接取模得到.
由于相位函数已知,因此可以直接以相位为图像矩阵作图,称之为原图.
以上数值模拟借助了数学软件Octave.
2)模拟中使用的相位物
模拟中用到的相位物是综合以上实验物体的特点设计的,突出了几种代表性相位物的特点,回避了实验中实际相位物的缺陷.包括:
a.文字.该物体具有锐利边缘,不同区域相移保持定值不变,笔画区相移为1,其他区域为0.对应实验中胶水涂敷的文字,但排除了其文字笔画区相移不均匀的缺点.
b.连续变化小相移物体.从左向右以正弦函数φ(x,y)=(sin x+1)/2变化,大小从左到右由0增加到1.与实验中超声光栅对应,但模拟中可以看出各种方法细节处的不同.
c.大相移的马鞍面.相移按φ(x,y)=xy变化,右上、左下两处顶角处为最大值100,右下、左上两处顶角处为最小值-100.这个物体主要是研究大相移,连续变化的相位物特点.实验中没有专门的物体对应.
3)模拟结果
模拟结果如图7~9所示.

图7 文字模拟图
数值模拟的结果很好地验证了前面对相衬法、暗场法和纹影法的分析:图9(a)和(c)中的条纹再一次说明对大相位物体成像的相衬法和暗场法的缺陷,而图9(a)和(c)在中心小相移区成像效果的不同说明相衬法对小相位细节信息的保留比暗场法更多;图8中(a)和(c)的亮度变化规律与理论预期一致;图7(d)和图9(d)中的立体效果是纹影法的特点.图7(b)和(d)中的多余阴影是由于离散化处理的误差引起的.
下面重点比较2种微分法的特点.
微分法成像公式比较简单,由式(9)确定,从图9(e)可以看出,所得结果是很严格的相位函数的方向差分的函数(此处选择了沿相位矩阵的主对角线做差分).从图7(e)看出具有边缘强化的效果,而且从图8(e)可以看出在小相移情况下成像结果比较好地反映了相位函数的微分.
而低频正弦光栅滤波的微分法与之相比共同点是,同样有边缘强化的效果,缺点是不如前者明显,这一点从式(14)与式(9)的比较以及图7(b)和(e)的对比可以看出;而且在遇到相位函数的变化不剧烈的情况时,成像结果不如后者,这一点可以从图8(b)和(e)的比较看出.

图8 相位按正弦函数变化的一维小相位物体模拟图
但是低频正弦光栅滤波的微分法相比微分法有其不具备的优点,前者干涉图像位于主光轴上,后者干涉图像位于主光轴外,而剩余大量光强都分布在主光轴上,这样的正弦光栅滤波器可以用于普通显微镜中,以实现对相位物的观察.目前,通常使用DIC显微镜观察相位物,它是靠Wollaston棱镜来实现微分法的,其成本较高,且对光源要求比较严格.正弦光栅滤波器只需要低频的光栅,对光栅分辨率要求低,可以使用普通胶卷制作,成本低廉,在普通实验室很容易获取,这是低频正弦光栅滤波微分法的最大优势.

图9 相位大小按马鞍面高度变化的相位物体模拟图
5 结 论
1)在较大相位,有锐利边缘时,相衬法和暗场法都会出现周期条纹,不适用.而纹影法和微分法是由相位变化率决定成像结果的,因此它们可以得到比较理想的成像结果.
2)相衬法是在微小相位情况下,各种方法中唯一对相位有线性响应的,因此最为适合观察微小相位物体,具体例子就是生物样品,适用于生物显微镜;对较大相位,相衬法会出现周期条纹,不适用,而且其滤波器制备和选择都较繁琐,这是其缺点.
3)暗场法亮度低,且与相位不成线性,但在定性观察中也很有用.与相衬法类似,暗场法也不适合大相位物体的观察.
4)纹影法是实现起来最方便的,而且像的亮度反映了此处相位变化快慢,但其缺点是难以同时得到较大的对比度和亮度.同时纹影法对大相位物体成像时不会产生条纹,是其优势.
5)微分法则是反映相位函数的差分的方法,复合型正弦光栅的缺点是浪费了大部分的光能在零级衍射点上,微分像亮度低.而且由于有效成像在一级衍射点,偏离主光轴,难以直接应用在普通显微镜中,必须用其他高成本的方案实现.
6)低频正弦光栅虽然最终成像由三重干涉决定,故与原始相位信息的对应关系较为复杂,但滤波器制作简单,且最终效果上保留了微分法的一个重要特点,即边缘强化的作用,因此它也不失为相位物可视化的一个好方法.
7)最后以上各种方法都有一个共同的缺点,不能严格定量测量[14],只适合定性观察.
[1] Zernike F.Phase contrast,a new method for the microscopic observation of transparent objects[J].Physica,1942,9(7):686-698.
[2] Goodmann J W.Introduction to fourier optics[M].New York:McGraw-Hill,1996:187-201.
[3] 钟锡华.现代光学基础[M].北京:北京大学出版社,2003:314.
[4] Hosch J W,Walters J P.High spatial resolution schlieren photography[J].Applied Optics,1977,16(2):473-482.
[5] Lohmann A W,Paris D P.Computer generated spatial filters for coherent optical data processiing[J].Applied Optics,1968,7(4):651-655.
[6] 黄妙娜,黄佐华.相位物体的相位检测分析方法[J].大学物理,2009,28(4):6-10.
[7] 黄妙娜,黄佐华,蔡文鑫,等.位相板的制作及其在相衬法实验中的应用[J].激光技术,2010,29(1):81-84.
[8] Huang Zuo-hua,Chen Feng-chao.A new method of scanning image for phase objects[J].Proc.SPIE,2006,6150(30):1-5.
[9] 潘元胜,冯璧华,于瑶.大学物理实验(第二册)[M].南京:南京大学出版社,2004:177-187.
[10] 郐新凯,郑亚茹.正弦光栅的制作[J].物理实验,2000,20(5):7-8.
[11] Leith E N,Swanson G,Leon S.Construction of diffractive optical elements in non-coherent light[J].Proc.SPIE,1984,503:2-8.
[12] 田宇,呼文来,徐雪楠.半导体激光器拍摄全息图的研究[J].物理实验,2010,30(8):24-26.
[13] 李芳菊,董康军.利用阿贝成像原理制作低频全息光栅[J].物理实验,2008,28(5):37-39.
[14] 张志利,徐毓娴,李文江.透明体的光学定量测量[J].光学技术,2001,27(2):146-149.

