一种基于HAMMER算法的软组织形变检测新方法*

马昂昂 廖琪梅 赵 菲② 卢虹冰

近年来，计算机辅助外科(CAS)技术广泛应用于神经外科、整形外科和耳鼻喉科手术。在这些手术领域，导航技术可以有效提高手术精确度，确保患者手术安全[1-2]。目前，也有研究小组在胸腹部手术中引入导航技术[3]。然而，由于受到呼吸、心跳、患者移动和手术操作的影响，在这类手术中，术前图像无法精确反映术中解剖结构的变化。虽然通过对术前模型及其性质的快速数学计算可以在一定程度上反映术中的形变，但这类工具还未能有效地应用于临床[4]。因此，必须获得术中影像数据以反映器官形变。

超声成像具有实时、无创的优点，因而广泛应用于临床诊断中[5]。但由于超声图像的分辨率和扫描区域因斑点噪声影响而受到局限，若能将术前器官组织高分辨率、高对比度的三维MRI图像和术中超声图像进行融合，可能是实现术中形变器官跟踪和软组织形变检测的有效方法[6]。虽然三维超声成像已成功应用于术中的实时导航，但目前相关研究主要集中在形变器官的跟踪和可视化方面，基于多模态影像的软组织形变检测和校正的研究相对开展较少[3]。

除了术中成像，另一个实现形变校正的关键问题是如何从多模态图像中检测到形变的器官，并对其产生的形变进行有效校正[7]。其中，作为一种高分辨率、基于体素的非刚性形态学配准方法，HAMMER算法利用从图像中派生出的属性向量，基于层次形变机制，实现了不同个体脑MRI图像的准确融合，具有很强的解剖结构检测和配准能力[8]。

本研究中，为了探索融合术前三维MRI图像和术中二维超声图像，进行腹部软组织器官形变检测和校正的可行性，通过利用微型电磁导航系统，结合改进的HAMMER算法，实现了一种形变检测和校正的新方法。该方法通过将MRI图像和超声图像进行配准和融合，对腹部软组织器官的形变进行检测和校正。为了定量评价所提出的方法，建立了超声图像计算机仿真模块，通过对腹部MRI图像进行刚性和非刚性形变，并利用形变后的MRI图像产生模拟的超声图像。在此基础上，结合电磁导航定位数据和改进的HAMMER算法，对形变的超声图像和原始MRI图像进行配准，同时采用平均位移和互信息对形变检测和校正的结果进行定量评价[9]。

1 方法和实验原理

1.1 软组织形变实时跟踪系统

在课题的前期研究中，建立软组织形变实时跟踪系统的框架和方法[10]。在这套系统中，通过将高分辨率的术前CT和(或)MRI图像、实时超声图像与电磁定位系统有机结合，初步实现了基于超声的软组织形变实时跟踪。基于该框架，可以对感兴趣区域软组织的三维结构和形变进行有效跟踪，从而提高腹部介入治疗、微创手术以及开放手术的精度。

1.2 超声图像的计算机仿真

在上述跟踪系统中，主要通过将二维超声探头与微型电磁定位系统结合，对探头及二维超声成像的位置进行定位，并注册到患者所在物理空间，实现术中成像的获取和定位。然而，由于术中人体的形变多样，获取数据的条件及环境因素复杂，如果直接利用术中数据，将会因缺乏真实的标准而很难对提出的方法进行有效评价[11]。为此，开发了超声图像计算机仿真模块，其目的是基于形变后的MRI图像而产生模拟的超声图像。

为了提高仿真图像的真实性，在超声图像计算机仿真过程中，需要建立两个重要的模型：超声采样模型和噪声模型[12]。其中，超声采样模型通过对超声束的发射以及回波采集过程的分析来模拟真实超声图像的获取过程。斑点噪声模型则是通过对图像施加符合一定统计规律的随机噪声来生成最终的超声图像。超声图像计算机仿真的流程如图1所示。

图1 超声图像计算机仿真的流程

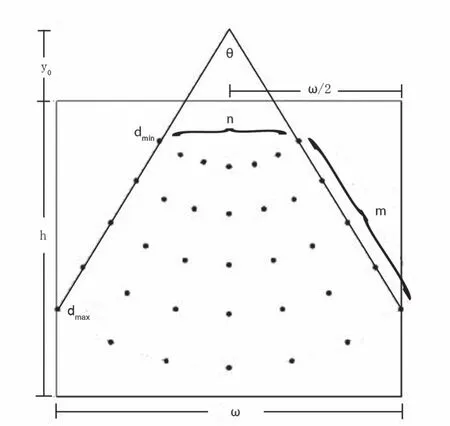
图2 超声图像采样过程

1.2.1 基于目标图像的超声采样

从目标图像(本实验中为MRI图像)中生成超声图像，其过程可通过计算发射超声波束与目标图像的交点，并进一步估计不同深度的超声回波值来模拟得到。整个采样算法的参数共有7个：①超声束数目n；②沿每条超声束方向上的采样点数目m；③扫描角度Θ；④图像宽度ω；⑤扇区原点高度y0；⑥轴向距离dmin；⑦轴向距离dmax。通过合理设置这些参数，可以模拟出具有真实感的超声图像。上述参数的定义和采样过程如图2所示。

从图2可以得出目标图像的笛卡尔坐标系(x,y)和超声采样点的极坐标系(ρ,θ)间的关系公式1：

1.2.2 插值

采样完成后需要对新图像中的空白点进行插值。考虑到超声图像的反射特性，本研究采用sin c函数作为卷积核[13]，如公式2所示，每个空白点的值由临近像素的卷积获得，临近像素对采样点的贡献由它们距采样点的距离x决定：

1.2.3 加噪

超声图像主要受乘性噪声影响，在乘性噪声中，斑点噪声被认为是超声图像退化的主要原因[14]。本研究中采用下面的模型公式3反映噪声对超声图像的影响：

其中，I(x,y)为原始未污染的图像，在本文中即为经过采样和插值后所得到的图像。I^(x,y)为噪声污染后的图像。ηm为斑点噪声，服从瑞利分布(见公式4)：

1.3 改进的HAMMER算法

Ding[15]提出的HAMMER算法是一种综合考虑图像灰度和几何结构特征的弹性配准算法。相较于其他配准算法，HAMMER的创新主要体现在两个方面：

(1)HAMMER算法在每个体素点上定义一个属性向量，以反映底层解剖结构的几何特性。在形变过程中，属性向量通过外形的相似性建立了解剖结构的一致性。每个属性向量a(x)由三部分组成：①边界类型；②灰度强度；③几何不变矩(GMIs)。

(2)HAMMER算法的层次形变机制。部分解剖结构有特定的形状特征，这些形状特征在初始化形变阶段被称为"锚点"，剩下的部分缓慢影响形变从而避免错误的目标。此外，在形变子空间时，形变机制形变图像相关的大部分不是单个体素，然后在整个子空间中估计属性向量的相似性，使得形变更加真实可信。有关于HAMMER算法更多的细节描述可以参见文献[4][8]。

考虑到软组织形变的非刚性以及多模图像强度分布的不同，在软组织的形变跟踪中，基于边缘特性的弹性配准方法应该更加适用[16]。有鉴于此，本研究选择HAMMER算法，用于软组织器官的形变检测和校正。

原HAMMER算法主要用于脑MRI单模态图像的配准，为了使HAMMER算法更适合MRI和腹部超声图像的配准，对算法做了相应的优化和改进。特别是每个体素的属性向量不再局限于GMIs，而是由一系列选定的属性组成，这些属性可从邻近像素计算得到。本实验中增加了像素强度、梯度幅值以及梯度幅值的方差作为属性向量。

2 实验和结果

2.1 MRI图像数据的采集

本实验的MRI图像源自第四军医大学附属西京医院放射科，采用3.0 T MR(MAGNETOM Trio, Siemens AG, Erlangen, Germany)扫描获得。扫描参数设置为：TR=250 ms，TE=2.3 ms，图像像素尺寸为256×256, 视野为220 mm, 层厚为1.00 mm。

2.2 MRI图像形变和超声图像仿真

为了模拟腹部不同形变的效果，对腹部肝脏MRI图像进行了如下3种几何变换，即旋转变换(逆时针旋转15o)，仿射变换(变换矩阵)和投影变换(变换矩阵)，其结果如图3所示：

图3 原始和形变的MRI图像

基于形变的MRI图像，通过超声图像计算机仿真，得到相应的模拟超声图像，如图4所示：

图4 模拟超声图像

为了实现对软组织形变的检测与校正，使用优化的HAMMER算法，分别对形变后的MRI图像和原始MRI图像以及模拟的形变超声图像和原始MRI图像进行配准，其结果如图5所示。

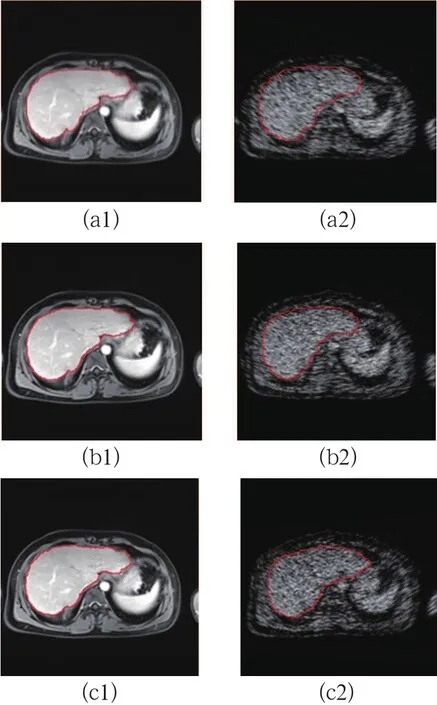
图5 配准结果

需要注意的是，HAMMER算法中需要确定一些参数，但其中最基本的参数就是整体搜索大小(δ)和当前迭代顺序(i)，其他参数则可进行相应估计。本实验中，依据经验，δ设置为9，i设置为25。图5示为经过相应校正后的MRI图像和超声图像。

(a1)-(a2)对旋转变换进行校正后的MRI和超声图像，(b1)-(b2)对仿射变换进行校正后的MRI和超声图像，(c1)-(c2)对投影变换进行校正后的MRI和超声图像为了定量评价形变检测和校正的效果，使用文献[17]中关于平均位移的计算方法分别计算不同变换条件下，校正前及校正后图像的平均位移，以定量评价形变校正的效果。其结果可以看出，经过配准和校正后，虽然对MRI单模图像的校正效果整体优于对MRI和US多模图像的校正，但是在3种变换下，校正后超声图像的平均位移均＜4个像素，图像形变得到很好的补偿(见表1)。

表1 形变图像和校正后图像的整体平均位移

由于系统的检测和校正过程涉及两种成像模态，为了进一步评价图像整体的校正效果，计算了原始MRI图像和校正后MRI图像、超声图像的互信息值(见表2)。

表2 原始图像和校正后图像的互信息值

3 结语

目前，在手术中软组织形变的检测和校正已经成为软组织导航技术的热点和难点问题。在研究中，提出一种新的软组织形变检测和校正方法，以改善跟踪和校正的效果。提出的新方法将术前MRI高分辨率图像和术中实时超声图像通过微型电磁定位系统有机结合，并利用改进的HAMMER算法对形变器官软组织进行检测和校正。基于平均位移和互信息的定量评价结果表明，所提出的新方法具有可行性。

在后续工作中，进一步拟将提出的新方法扩展至三维图像，并利用临床实时超声扫描数据和定位信息，对提出新方法的临床可行性进行验证。此外，提出的新方法还将与导航系统硬件相结合，将进一步开发软组织导航系统。

[1]Xing L,Thorndyke B,Schreibmann E,et al. Overview of image-guided radiation therapy[J]. Med Dosim,2006,31(2):91-112.

[2]Pluim JP, Fitzpatrick JM. Image registration[J]. IEEE Trans Med Imaging,2003,22(11):1341-1343.

[3]Wein W,Brunke S,Khamene A,et al.Automatic CT-ultrasound registration for diagnostic imaging and image-guided intervention[J].Med Image Anal,2008,12(5):577-585.

[4]Shevchenko N, Schwaiger J, Markert M, et al. Evaluation of a resectable ultrasound liver phantom for testing of surgical navigation systems[J].Conf Proc IEEE Eng Med Biol Soc,2011,2011:916-919.

[5]Siddiq A, El Sayed T.Ultrasonic-assisted manufacturing processes: variational model and numerical simulations[J]. Ultrasonics,2011,52(4):521-529.

[6]Coenegrachts K. Magnetic resonance imaging of the liver: New imaging strategies for evaluating focal liver lesions[J].World J Radiol,2009,1(1):72-85.

[7]Xu HX,Lu MD,Liu LN,et al.Magnetic n a v i g a t i o n i n u l t r a s o u n d-g u i d e d interventional radiology procedures[J].Clin Radiol,2011,67(5):447-454.

[8]Ding GS,Christos D,HAMMER:hierarchical attribute matching mechanism for elastic registration[J].IEEE Transactions on Medical Imaging,2001,21:1421-1439.

[9]罗建文,范宇,白净.基于位移量的软组织应变测量快速算法[J].声学学报(中文版),2002,27(1):18-22.

[10]马宝秋.基于实时超声影像的软组织形变跟踪技术[D].西安:第四军医大学,2010.

[11]Mazza E, Barbarino GG. 3D mechanical modeling of facial soft tissue for surgery simulation[J].Facial Plast Surg Clin North Am,2011,19(4):623-637.

[12]张伟志,刚铁,王军.超声波检测计算机模拟和仿真的研究及应用现状[J].应用声学,2003,22(3):39-44.

[13]Huang QH,Zheng YP, Lu MH, et al. Development of a portable 3D ultrasound imaging system for musculoskeletal tissues[J]. Ultrasonics,2005,43(3):153-163.

[14]Hiremath PS, Prema TA, Sharan B. Speckle Reducing Contour let Transform for Medical Ultrasound Images[J].International Journal of Computer and Information Engineering,2010,4(4):284-291.

[15]Ding GS. Image registration by hierarchical matching of local spatial intensity histograms[C].Medical Image Computing and Computer Assisted Intervention,France, 2004:582-590.

[16]Taylor ZA, Comas O, Cheng M, et al. Modelling anisotropic viscoelasticity for real-time soft tissue simulation[J]. Med Image Comput Comput Assist Interv,2008,11(1):703-710.

[17]Robert H, Zdenko B, Martin H. Methodology for determination of modal parameters by digital image correlation[C].Modelling of mechanical and mechatronic systems 2011,Slovak Republic,2011:193-201.