基于经验模态分解的上证综合指数时间序列分析

蔡赟姝， 卢志明

(上海大学上海市应用数学和力学研究所，上海200072)

中国的证券市场，以1990年12月上海证券交易所和1991年4月深圳证券交易所开始营业为标志，已走过了20多年的发展历程.作为一个新兴的发展中市场，其市场结构、市场规则等方面还不够成熟、规范.证券市场的稳定对于金融市场乃至整个国民经济的平稳运行都具有非常重要的意义，因此，研究股票指数的变化规律及波动特性，无论是对政府部门还是对投资者都具有重要意义.股票指数是非线性、非平稳的时间序列.我国股市数据具有时间序列短、随机因素多、价格波动变化剧烈等特点［1］.这些特点对金融时间序列的分析提出了较高的要求，在其实证研究中需要一种更为有效的方法或工具.

近年来，金融领域的跨学科研究受到了广泛关注，许多学者将数学、物理学以及工程等领域的理论、方法、技术等运用于金融时间序列的研究，并取得了丰硕的成果［2-3］.信号分析技术作为其中的一种有力工具，已被运用于金融时间序列的分析中.经验模态分解(empirical mode decomposition，EMD)方法是Huang等［4］于1998年首次提出的一种新的信号处理方法.1999年，Huang等［5］又对该方法进行了改进.与以往的信号分析方法不同，EMD方法并不预设基函数，而是预先选择好判据，基于信号本身所包含的特征尺度进行分解，得到有限阶内模函数(intrinsic mode functions，IMFs).EMD方法对数据没有平稳性和线性的要求，具有自适应性的特点，能更好地保留原有信号的特征.该方法是对传统信号分析方法的发展和突破，已在自然科学、工程等领域引起了广泛的关注［5-7］，并在非线性、非平稳数据处理中得到了更符合物理实际的解释和说明.2003年，Huang等［8］首次将该方法引入金融时序的分析.此后，国内外一些学者也陆续尝试将该方法用于石油价格预测［9］、经济增长波动［10］、股指日收益率［11］等金融领域的研究，取得了较好的效果.本研究主要将该方法用于上证综合指数(Shanghai composite index，SCI)时间序列的分析.对于上证综合指数已有较多的研究，如自回归(autoregressive，AR)模型，自回归滑动平均(autoregressive moving average，ARMA)模型、单位根在内的差分模型以及自回归条件异方差(autoregressive conditional heteroskedasticity，ARCH)模型、广义自回归条件异方差(generalised autoregressive conditional heteroskedasticity，GARCH)模型等［12-13］，也获得了较好的波动特点和统计结果，但这些分析方法往往是在单一尺度上进行的，而基于EMD方法的多尺度分析更能捕捉到上证综合指数不同尺度的波动特点和统计特性.

1 EMD方法简介

内模函数描述性定义［4-5］由以下 2点给出：①极值点的个数和过零点的数目相等，或者最多相差为1;②在任意一点，由极大值和极小值构成的包络的平均值为0.为了从原始信号中分解出内模函数，Huang等［4］给出了经验模态分解方法，过程如下：①找到信号x(t)所有的极值点;②用3次样条曲线拟合出上下极值点的包络线emax(t)和emin(t)，并求出上下包络线的平均值，即m(t)=(emax(t)+ emin(t))/2，并在x(t)中减去它，即h(t)=x(t)-m(t);③根据预设判据，判断h(t)是否为IMFs，如果不是，则以h(t)代替x(t)，重复步骤①和步骤②，直到h(t)满足判据，则h(t)即为需要提取的内模函数Ck(t);④每得到一阶IMFs，就从原信号中将其扣除，重复以步骤①～步骤③，直到信号最后剩余部分rn(t)为单调序列或者常值序列.

经过EMD方法分解，将原始信号x(t)分解成了一系列IMFs以及剩余部分的线性叠加，即

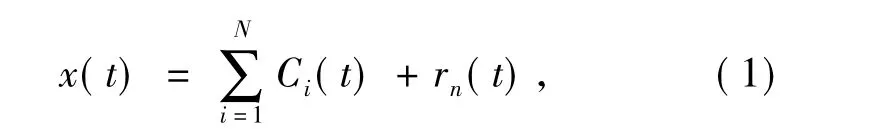
式中，Ci(t)为第i阶IMF.Huang等［4］将这样的处理过程形象地比喻为“筛”过程(sifting process).最后，原始数据序列可用这些IMFs分量以及一个均值或趋势来表示.由于每一个IMFs分量代表一组特征尺度的数据序列，“筛”过程实际上是将原始数据序列分解为各种不同特征波形的叠加，每一个IMFs分量既可以是线性的也可以是非线性的.图1为IMFs例子.

图1 IMFs例子Fig.1 Example of IMFs

2 股票指数时序的EMD分解与分析

股票指数是典型的非线性、非平稳的金融时间序列，尤其是处于成长期的我国股市数据，更具有时间序列短、随机因素多、价格波动变化剧烈等特点.股票指数时间序列分析方法应与普通的信号处理方法有所不同.因此，本研究尝试将EMD方法用于上证综合指数日收盘价数据的处理和分析.

2.1 上证综合日指数的EMD分解

本研究数据主要采用上证综合指数(000001).该指数从总体上反映了上海证券交易所上市股票的价格变动情况.数据来源于新浪财经，主要针对1994年之后上证综合指数日收盘价数据、典型的上涨和下跌时间段的日收盘价数据进行EMD分解及分析.

对1994年1月3日—2010年9月30日上证综合指数，共4 074个交易日的日收盘价格数据进行EMD分解，共得到了9阶内模函数和剩余项，如图2所示.可以发现，IMFs按频率由高到低排列，分解得到的剩余部分是单调的趋势项.因此，用EMD方法对金融时间序列进行处理，可以将原时间序列分解为不同尺度的分量，进而通过对分量的研究达到研究原序列的目的.

图2 上证综合指数4 074个交易日收盘价格数据的EMD分解结果Fig.2 EMD results of closing price data of SCI(4 074 trading days)

IMF1的高频振荡能很好地刻画上证综合指数的波动细节.直观上可以看出，原序列的波动都能从IMF1中找到.可见，IMF1反映的是上证综合指数日线的波动细节.IMF2，IMF3能刻画上证综合指数日线频率较高的波动.IMF4，IMF5能刻画上证综合指数日线中的高频波动，但与IMF1～IMF4相比，其反映的波动细节要少.同时发现，在2006年下半年附近的波动幅度比之前的波动要明显.IMF6～IMF9各模态的波动频率低于IMF1～IMF5，其波动尺度也较大，在2007年底2008年初附近有较大幅度的波动.观察剩余项，发现其并不反映上证综合指数日线的波动，而是一条反映大体上升趋势的曲线.

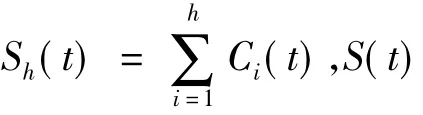
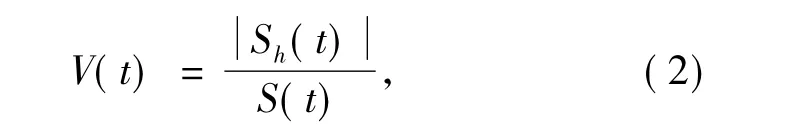
1994年1月3日—2010年9月30日上证综合指数日收盘价数据，经EMD分解重构后的波动和波动率如图3所示.可见，在1994—1996年，波动幅度比较大，其原因主要是当时我国股市正处于起步阶段，市场较不稳定，加之我国证券市场现行的涨跌停板制度是从1996年12月26日才开始实施的.这在先前仅仅通过模态重构的绝对波动图中是无法发现的.在2006—2009年期间，波动幅度也比较大.在这期间，中国股市经历了从未有过的大涨和大跌，2007年10月中旬一度达到6 000多点的高位.这一过程无论在波动率的图中还是在各阶模态中都有所体现，在此期间，股市具有较大的能量.

2.2 上证综合指数及其IMF的统计分析

对上证综合指数1994年1月3日—2010年9月30日的日收盘价格数据进行EMD分解，并对分解后的各阶IMFs进行白噪声显著性检验［14］，以判断是否存在只包含噪声而无其他信息的模态，结果如图4所示，其中虚线为白噪声理论线，实线为95%置信水平线，9个点分别代表实证数据IMF1～IMF9的检验值.可见，这些值均在实线上方，表明在95%置信水平下，各阶IMFs与白噪声相比是显著的，上证综合日指数经EMD分解后得到的各阶IMFs都不是白噪声，包含有一定的实际物理(经济学)信息.

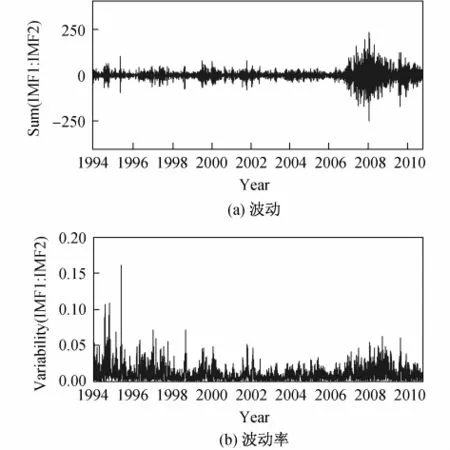
图3 上证综合指数日收盘价格数据经EMD分解重构后的IMF1～IMF2的波动和波动率Fig.3 Volatility and variability of closing price data of SCI based on the IMF1～IMF2

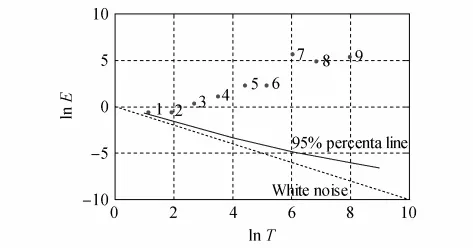
图4 各阶IMFs的白噪声显著性检验Fig.4 Significance test of IMFs of white noise

对各阶IMFs进行基本统计分析，发现样本偏斜度基本对称，峰度绝大部分均大于3.与正态分布相比，各阶模态呈现“尖峰厚尾”的现象.这一结果的意义在于，大致确定了上证综合指数各不同频率数据的分布形状.

由于t分布的概率密度函数比正态分布具有更厚的尾部，因此，尝试用t分布来描述各阶IMFs的厚尾特性.自由度为n的t分布的概率密度函数为

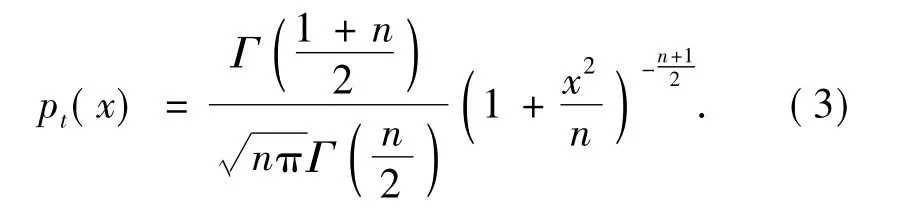
绘制Quantiles-Quantiles(Q-Q)图对数据进行拟合，实证数据根据理论分布绘制出的点应近似为一条直线，任何偏离这条直线的点都是偏离了该规定的分布.图5为用正态分布绘制的IMF1和IMF2的Q-Q图，可见明显不在一条直线上.图6为自由度n=3的t分布(记为t(3))的Q-Q图，可见，除了端部，几乎都在一条直线上.其他各阶IMFs也有类似结果.通过对比Q-Q图可以发现，用t(3)分布拟合好于用正态分布拟合.

图5 基于正态分布的上证综合日指数IMF1和IMF2的Q-Q图Fig.5 Q-Q plot of IMF1 and IMF2 of SCI based on normal distribution

2.3 上证综合指数及其IMFs的周期性分析

通过观察上证综合指数的EMD分解结果，可以发现，上证综合指数及其IMFs的变动有一定的周期性，并且不同的IMFs反映了不同时间尺度上的波动信息.例如，对上证综合日指数收盘价数据经EMD分解后的各阶IMFs进行重构，通过IMF3+IMF4+ IMF5+IMF6+IMF7+IMF8+IMF9+RES所得的曲线(见图7(a))与计算得到的周平均指数曲线(见图7(b))相似;通过 IMF5+IMF6+IMF7+IMF8+ IMF9+RES所得的曲线与计算所得的月平均指数曲线类似.这表明，EMD方法能够提取金融时序中不同波动周期的分量.研究股市波动的各个周期，了解上证综合指数的各种周期特征，无论是对于投资者还是政府部门都具有非常大的现实意义.

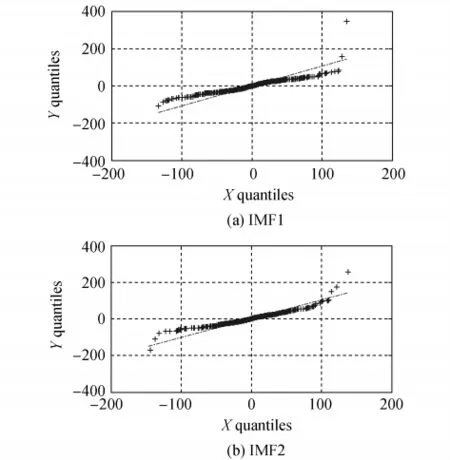
图6 基于t(3)分布的上证综合日指数IMF1和IMF2的Q-Q图Fig.6 Q-Q plot of IMF1 and IMF2 of SCI based on t(3)distribution

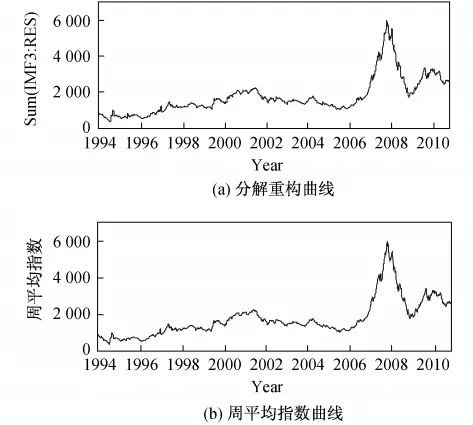
图7 重构的IMF3～RES所得曲线和周平均指数曲线Fig.7 Curves of reconstruction of the data from the sum of IMF3～RES and weekly averaged index

本研究运用平均周期法来计算上证综合指数经EMD分解后的各阶IMFs的周期.平均周期法是根据波峰和波谷的数目给出上证综合指数的震荡周期，即

式中，N1为时间序列中的数据点个数，N2为极大值点个数或极小值点个数.

通过计算1994年1月3日—2010年9月30日上证综合日指数经EMD分解后的各阶IMFs的周期(见表1)，发现各时间尺度依次递增，其中IMF2，IMF4和IMF6的平均周期分别为6.870，33.950和162.960 d，表明这3个模态大致反映了周、月和半年尺度上的波动.

表1 上证综合指数各阶IMFs的周期Table 1 Periods of the IMFs of SCI

此外，通过对上证综合指数上涨阶段(2005年12月12日—2007年10月15日)和下跌阶段(2007年10月24日—2008年10月16日)的日收盘价数据进行周期性分析，发现在上涨和下跌过程中，各阶IMFs具有较好的周期性特征，具体结果如表2所示.为进一步观察典型的上涨和下跌过程的波动特点，绘制了这两个阶段的波动率图(见图8).可以看到，上涨初期的波动幅度比较小，随着上涨过程的推进，幅度逐渐增大;下跌过程则表现出更为明显的震荡，且幅度大于上涨过程.结合各阶IMFs的周期、标准差(见表3)及波动率等结果，从整体指数走势来看，指数下跌过程快于上涨过程，且下跌时间段各阶IMFs的周期、波幅均大于上涨时间段，其差值也随着IMFs阶数的增大逐渐增大.

表2 上证综合指数典型上涨和下跌阶段各阶IMFs的周期Table 2 Periods of the IMFs on typical rising and dropping processes of SCI

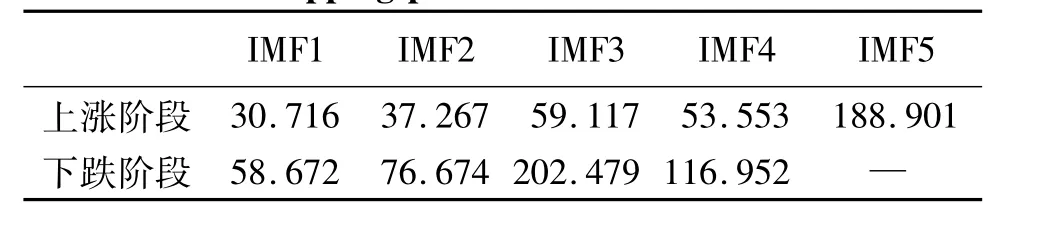
表3 上证综合指数典型上涨和下跌阶段各阶IMFs的标准差Table 3 Standard deviations of the IMFs on typical rising and dropping processes of SCI

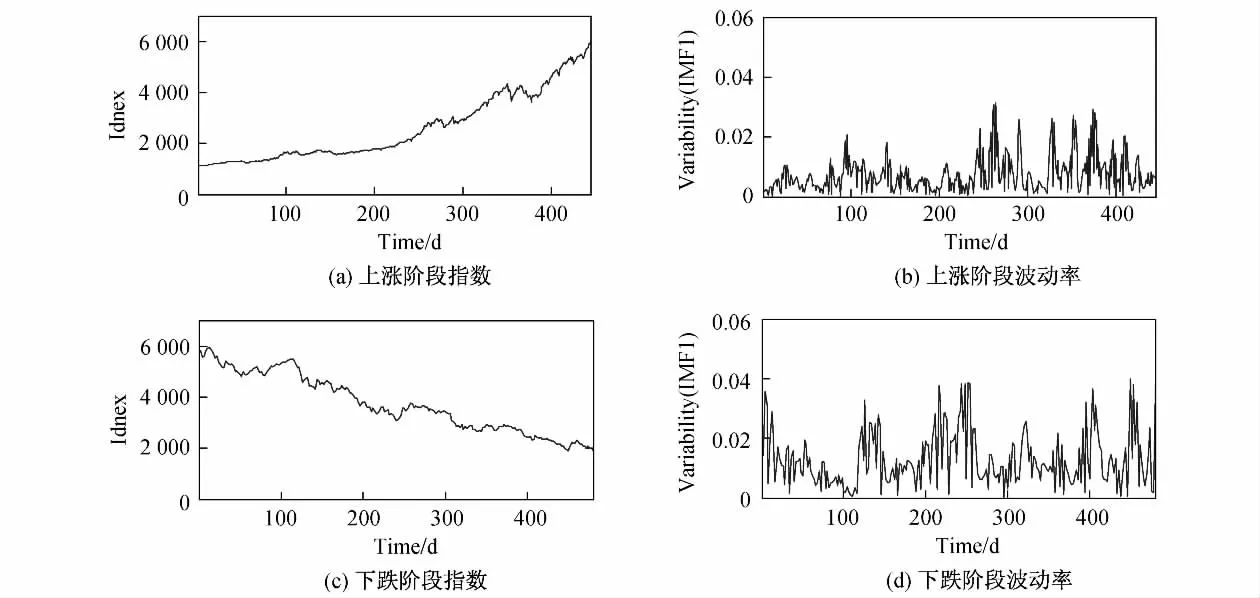
图8 上证综合指数典型上涨和下跌阶段的指数和波动率Fig.8 Index and variability on typical rising and dropping processes of SCI

3 结束语

EMD方法基于信号本身所包含的尺度进行分解，具有良好的自适应性，对数据没有线性和平稳性的要求.本研究将EMD方法用于非线性、非平稳特性的金融时间序列分析，将上证综合日收盘价指数分解为多个不同尺度的IMFs和剩余项.研究结果表明，通过对分解后各阶IMFs进行白噪声显著性检验，发现并不存在白噪声的模态，各模态包含着一定的实际物理(经济学)信息.随后，对各模态进行基本统计分析和分布拟合，发现其“尖峰厚尾”的特点基本服从自由度为3的t分布.通过对各阶IMFs进行周期性分析，运用平均周期法计算各阶IMFs的周期，揭示了各阶模态间不同的波动信息，并得到了周、月、半年等相关时间尺度的波动特点，这表明EMD方法可以有效地提取金融时序中不同波动周期的分量.此外，对典型上涨和下跌阶段的周期性进行了分析，发现不同尺度的模态在这两个阶段都具有较好的周期性特点，上涨初期的波动幅度比较小，随着上涨过程的推进，幅度逐渐增大.从整体指数走势来看，指数下跌过程快于上涨过程，且下跌时间段各阶IMFs的周期、波幅均大于上涨时间段.

［1］ 韩仙华，蒋敏.金融系统复杂性与经济物理学模型——物理-经济-股市：股市波动的经济物理学分析［J］.系统辩证学学报，2002，10(3)：35-39.

［2］ GABAIXX，GOPIKRISHNANP，PLEROUV，et al.A theory of power-law distributions in financial market fluctuations［J］.Nature，2003，423(6937)：267-270.

［3］ PLEROU V， GOPIKRISHNAN P，STANLEY H E.Econophysics：two-phase behaviour of financial markets［J］.Nature，2003，421(6919)：130.

［4］ HUANGN E，SHENZ，LONGS R，et al.The empirical mode decomposition and the Hilbertspectrum for nonlinear and non-stationary time series analysis［J］.Proceedings：Mathematical，Physical and Engineering Sciences，1998，454(1971)：903-995.

［5］ HUANGN E，SHENZ，LONGS R.A new view of nonlinear water waves：the Hilbert spectrum［J］.Annual Review of Fluid Mechanics，1999，31(1)：417-457.

［6］ DUFFYD G.The application of Hilbert-Huang transforms to meteorological datasets［J］.Journal of Atmospheric and Oceanic Technology，2004，21(4)：599-611.

［7］ HUANGY X，SCHMITTF G，LUZ M，et al.An amplitude-frequency study of turbulent scaling intermittency using empirical mode decomposition and Hilbert spectral analysis［J］.Europhysics Letters，2008，84(4)：40010.

［8］ HUANGN E，WUM L，QUW，et al.Applications of Hilbert-Huang transform to non-stationary financial time series analysis［J］.Applied Stochastic Models in Business and Industry，2003，19(3)：245-268.

［9］ YUL，LAIK，WANGS，et al.Oil price forecasting with an EMD-based multiscale neuralnetwork learning paradigm［C］∥ The InternationalConference on Computational Science.2007：925-932.

［10］ 秦贤宏，段学军，李慧.基于EMD的我国经济增长波动多尺度分析［J］.地理与地理信息科学，2008，24 (2)：44-47.

［11］ 丁志宏，谢国权.金融时间序列多分辨率实证研究的EMD方法［J］.经济研究导刊，2009(6)：61-63.

［12］ 陈志娟.上证指数收益率的ARCH族型的实证分析［J］.统计与决策，2010(17)：141-143.

［13］ 孔祥芝，王延清.基于ARIMA-GARCH模型和极值理论的中国股市［J］.中国管理信息化，2010(9)：57-60.

［14］ WUZ H，HUANGN E.A study of the characteristics of white noise using the empirical mode decomposition method［J］.Proceedings of the Royal Society of London SeriesA：Mathematical，Physicaland Engineering Sciences，2004，460(2046)：1597-1611.