Sylvester型泛函的极值问题
王广廷
(上海大学理学院,上海200444)
设κn表示n维欧氏空间Rn中凸体的集合.对于K∈κn,泛函
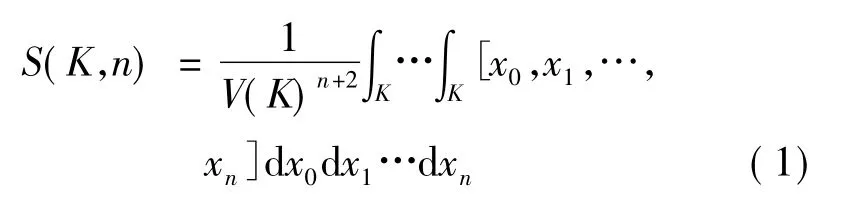
表示随机单形的体积的平均期望,其中V(K)表示K的体积,[x0,x1,…,xn]表示x0,x1,…,xn的凸包的体积.Sylvester问题是:寻找使得S(K,n)取得最大值和最小值的凸体.Blaschke[1]解决了当n=2时的情况,即椭圆是S(K,2)取得最小值的唯一凸体,三角形是S(K,2)取得最大值的唯一凸体.当n>2时,Groemer[2]证明了椭球是使S(K,n)取得最小值的唯一凸体.寻找使得S(K,n)取得最大值的凸体,至今仍是一个公开问题.数学家们猜想,单形是S(K,n)取得最大值的唯一凸体.
Groemer给出了Sylvester泛函的一个自然的推广,他考虑了如下形式的泛函:
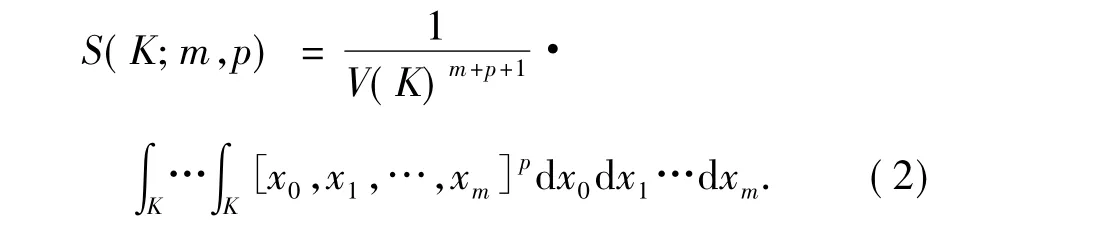
Groemer[3]证明了当 m≥n及 p≥1时,椭球是使S(K;m,p)取得最小值的唯一凸体.当p>0及m=n时,Schöpf[4]得到了相同的结果.当n=2时,Dalla等[5]证明了三角形可使 S(K;m,1)取得最大值.Giannopoulos[6]证明了三角形是使S(K;m,1)取得最大值的唯一凸体.
对于K∈κn,支撑函数hK由下式定义:
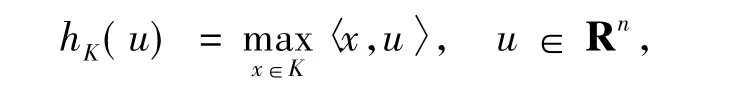
式中,〈·〉表示标准内积.
设凸函数φ:R→[0,∞),使得φ(0)=0,则φ在(-∞,0]内递减,在[0,∞)内递增.设函数φ或者在(-∞,0]内严格递减,或者在[0,∞)内严格递增,用C表示这一族函数.
假定K为Rn中包含原点为其内点的凸体,凸体K的Orlicz质心体Γφ(K)[7]为Rn中的一个凸体,其支撑函数由下式定义:
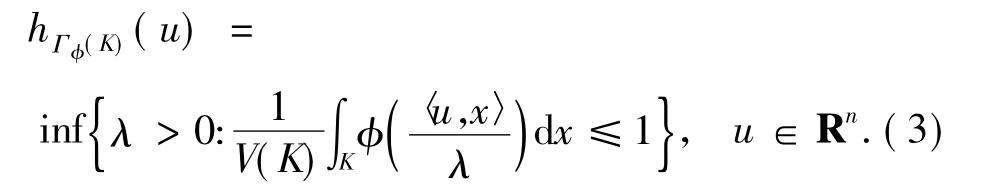
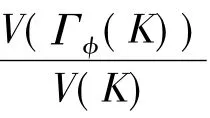
本工作将研究如下泛函:
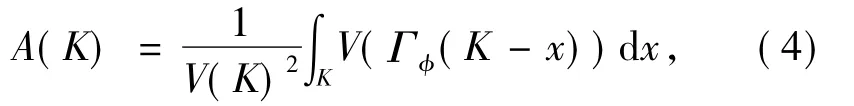
并应用影子系统[8-9]证明主要定理.给定一个方向v和任意一个指标集I,使得对每个i∈I,ai为Rn中有界子集A中的一个点.沿着方向v的一个影子系统为Rn中的一族凸体Kt,其定义为
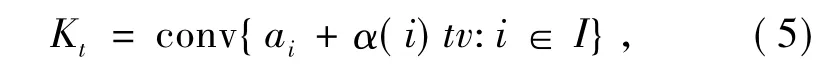
式中,α为定义在I上的有界实值函数,t为时间参数,t∈[t1,t2],α(i)为点ai沿v方向的速度函数.
影子系统可以看作是一个给定集合的连续变换过程.一个特殊的影子系统是凸体的Steiner对称.此时,速度函数α:K→R在每一个平行于方向v的弦上是常数,在每个时间t,这些弦的并就是Kt,具有这种性质的影子系统称为平行弦运动.平行弦运动保持体积不变.如果平行弦运动的速度函数α:K→R是一个仿射函数,即α(x)=〈x,u〉+c,其中u∈v⊥,c∈R,那么对每个t,Kt为K的一个仿射象.
1 A(K)的极值
Rogers等[8]证明了如下引理.
引理1 一个影子系统的体积V(Kt)是t的凸函数.
Li等[10]证明了如下定理,它在研究泛函A(K)的极值问题中起到重要作用.
引理2 如果{Kt:t∈[0,1]}是沿着方向v的平行弦运动,则Γφ(Kt)是沿着方向v的影子系统,并且V(Γφ(Kt))是关于t的严格凸函数,除非速度函数α(x)=〈x,u〉.
由式(3)和(4)容易得到如下的引理3.
引理3 A(K)在Hausdorff度量下关于K连续.
引理4 A(K)是仿射不变的.
证明 设T∈GL(n)为一个线性映射,由式(3)可得

式中,TT为T的转置矩阵.另一方面由支撑函数的定义,有
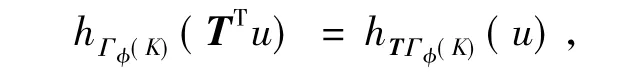
因此,Γφ(TK)=TΓφ(K).所以
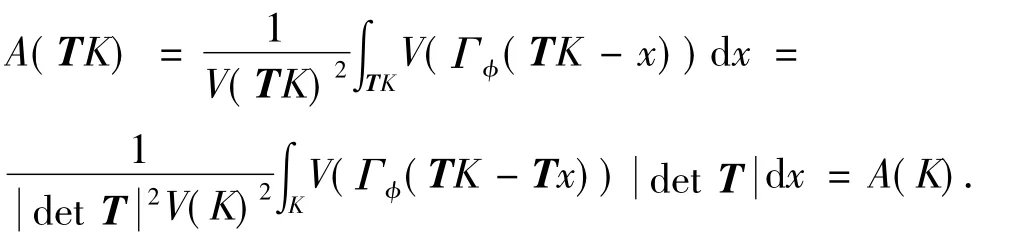
又因为A(K)是平移不变的,因此,A(K)是仿射不变的.
定理1 如果Kt:t∈[0,1]是一个平行弦运动,则A(Kt)是t的凸函数,并且A(Kt)是严格凸的,除非速度函数是一个仿射函数.
证明 设平行弦运动的速度函数为α,运动方向为v,则
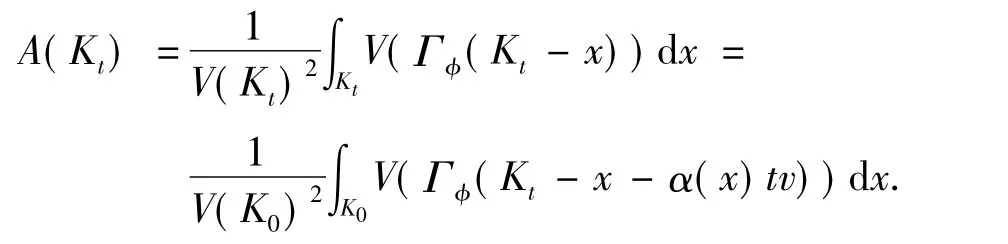
设
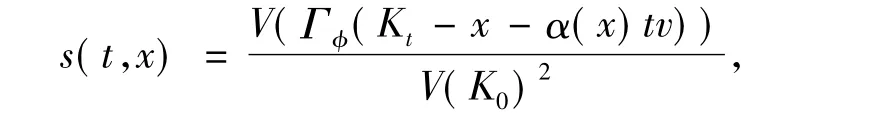
则
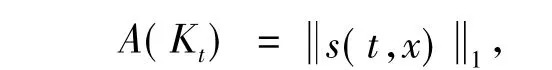
式中,s(t,x)1取值于 L1(K0).对每个 x∈K0,{Kt-x-α(x)tv:t∈[0,1]}为具有速度函数α(·)-α(x)的平行弦运动,因此,由引理2知,s(t,x)为关于t的凸函数.
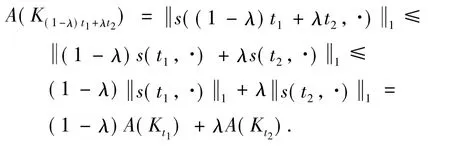
由L1范数的Minkowski不等式,有引理2表明,上述第一个不等式当且仅当α为一个仿射函数时取得,此时的α(z)-α(x)=〈z-x,u〉,其中u∈v⊥.这时,s(t,x)为关于t的常值函数,上式等号处处成立.
定理2 在所有的凸体中,A(K)取得最小值,当且仅当K是一个椭球.
证明 固定一个方向v,设K∈κn为一个凸体.用K|v⊥表示K在v⊥上的正交投影,则K可以表示为
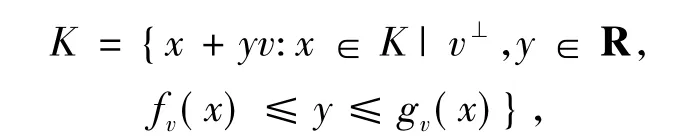
式中,fv,-gv为定义在v⊥上的凸函数.
凸体K关于v⊥的Steiner对称可以用平行弦运动描述如下:在式(5)中,取α(x)=-(fv(x|v⊥)+ gv(x|v⊥)),t∈[0,1];当t=0时,Kt=K;当t=1时,Kt=Kv,其中Kv为K关于v⊥的反射;当t=时,Kt为K关于v⊥的Steiner对称.
A(K)在K和Kv取得相同的值.由定理1知,在A(K)从K变为K的Steiner对称的过程中是不增的,并且A(K)是严格递减的,除非平行弦运动的速度函数是一个仿射函数,即K的平行与v方向的弦的中点位于一个超平面上.Petty[11]证明了椭球是具有这种性质的唯一凸体.
注意到A(K)是定义在紧集上的连续函数,A(K)的最小值存在.由 A(K)的仿射不变性知,A(K)在椭球上取常数值.
如下的定理3给出了A(K)在n=2时的最大值.
定理3 当n=2时,在所有凸体中,A(K)取得最大值当且仅当K是一个三角形.
证明 由A(K)的连续性,只需证明在所有的多边形中,三角形使A(K)取得最大值.设P为一个具有n≥3个顶点的多边形,v1,v2,v3为P的3个连续的顶点,u为平行于v1和v3连线的方向,{Pt:t∈[t0,t1]},t0<0<t1为沿着u方向的影子系统,并且Pt在v2的速度为1,在其余顶点的速度为0.如果t和t1充分接近0,则多边形P中除三角形v1v2v3外,其余均保持不动.设[t0,t1]是使Pt,t∈[t0,t1]的面积保持不变的最大区间.因此,{Pt:t∈[t0,t1]}是平行弦运动的,且Pt0和Pt1有n-1个顶点.由定理1知,
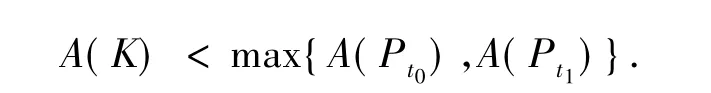
由于平行弦运动的速度函数不是仿射函数,因此,上述不等式中的不等号是严格成立的.当n>4时,重复上述过程可得,三角形使得A(K)取得最大值.
用类似于定理3的方法,有如下的定理4.
定理4 当n=2时,在所有中心对称的凸体中,A(K)取得最大值当且仅当 K是一个平行四边形.
[1] BLASCHKEW.Uber affine geometrieⅪ:lösung des“ierpunktproblems”von sylvester aus der theorie der geometrischen wahrscheinlichkeiten [J]. Leipziger Berichte,1917,69:309-317.
[2] GROEMERH.On some mean value associated with a randomly selected simplex in a convex set[J].Pac J Math,1973,45:525-533.
[3] GROEMERH.On the mean value of the volume a randomly polytope in a convex set[J].Arch Math,1974,25:86-90.
[4] SCHÖPFP.Gewichtete volum smittelwerte von simplices,welche zufällig in einem konvexen Körper des Rngewählt warden[J].Mh Math,1977,83:331-337.
[5] DALLAL,LARMAND G.Volumes of a random polytope in a convx set[M]∥ GRITZMANNP,STURMFELSB.DIMACS:series in discrete mathematics and theoretical computer science.Washington:American Mathematics Society,1991:175-180.
[6] GIANNOPOULOSA A.On the mean value of the area of a random polygon in a plane convex body [J].Mathematika,1992,39:279-290.
[7] LUTWAKE,YANGD,ZHANGG.Orlicz centroid bodies[J].J Differential Geom,2010,84:365-387.
[8] ROGERSC A,SHEPHARDG C.Some extremal problems for convex bodies[J].Mathematika,1958,5:93-102.
[9] SHEPHARDG C.Shadow systems of convex bodies[J].Israel J Math,1964,2:229-236.
[10] LIA,LENGG.A new proof of the Orlicz Busemann-Petty centroid inqualities[J].Proc AMS,2011,139:1473-1481.
[11] PETTYC M.Isoperimetric problems[C]∥ Proceedings of Conference Convexity and Comnibatorial Geometry.1972:26-41.

