内积空间上的拉格朗日型矩阵有理插值

顾传青， 张 科， 王 锋

(上海大学理学院，上海200444)

矩阵有理插值问题包括矩阵幂级数的部分实现问题和Newton-Padé，Hermite-Padé，多点Padé逼近及其矩阵形式的推广等问题［1］.已有的工作研究了利用相同插值点的矩阵有理逼近问题.Antoulas等［2］解决了最小矩阵有理插值问题.Anderson等［3］利用Loewner矩阵，研究了实有理传递函数矩阵的插值数据，传到传递函数矩阵的一个最小状态变量的实现问题.Gu［4］给出了一种广义逆矩阵有理插值(generalized inverse matrix rationalinterpolation，GMRI)法，该方法推广并提高了Graves-Morris等［5-6］的广义逆向量有理插值法，使得构造过程中不必计算矩阵的乘法.但是GMRI法受次数和可除性的限制，构造的有理插值式中的分母多项式的次数不能是奇数［4，7-8］.利用牛顿多项式，Sidi［9-10］给出了3种不同的向量插值型有理插值式，其分子为向量值多项式，分母为标量多项式.

本研究的目的是为了改进GMRI法，通过构造一种新的以拉格朗日多项式为基础的迭代关系，提出了内积空间上一种基于拉格朗日型矩阵有理插值的实用方法.利用矩阵内积，给出3种不同的标准来得到3种有理插值方法.这类方法最早由Sidi［9-10］提出并讨论了牛顿向量值有理插值问题.在此基础上，Gu［11］研究了矩阵Padé型逼近问题.

1 矩阵值有理插值的一般方法

设z为一复变量，F(z)为矩阵值函数，即F：C→ Cs×t.假定F(z)定义在有界开集Ω上，现考虑F(z)在插值节点z1，z2，…处的插值问题，假定这些插值点是互异的.

令Lm，n(z)为函数F(z)在点zm，zm+1，…，zn处的矩阵值插值多项式，其次数最多为n-m.利用拉格朗日多项式，有

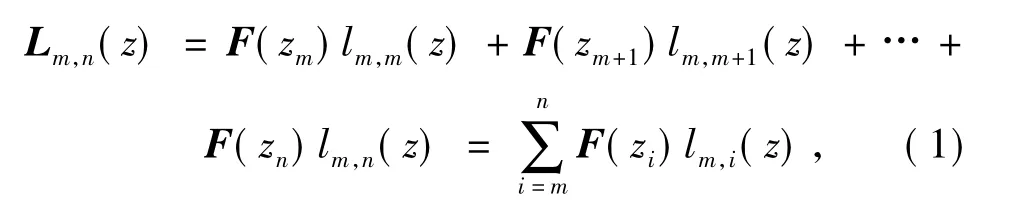
式中，lm，i(z)为拉格朗日基函数，即

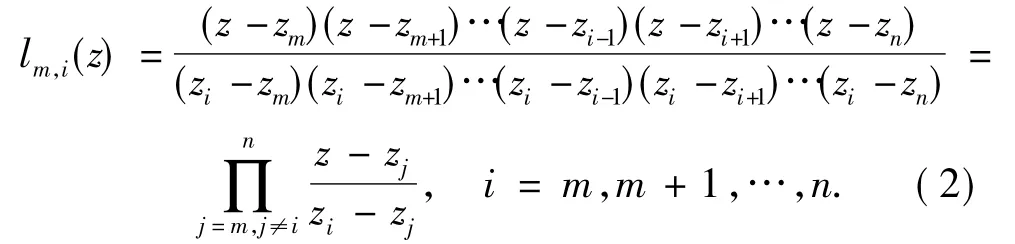
显然，Lm，n(z)∈Cs×t.为简洁起见，将数量多项式Wm，n(z)表述为

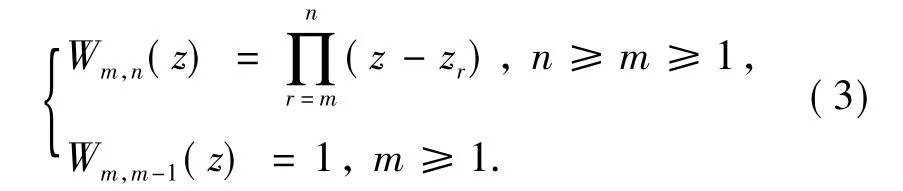
利用上述符号，定义一类矩阵值有理函数Rl，k(z)为

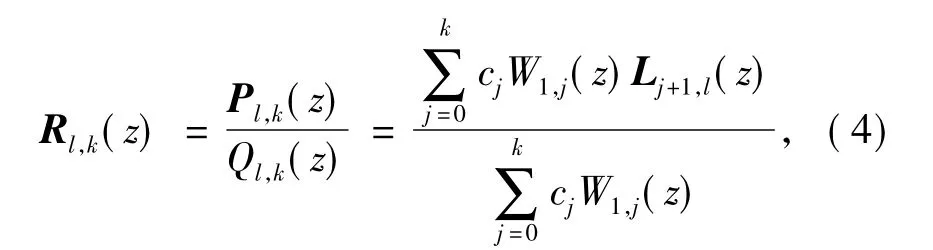
式中，c0，c1，…，ck为任意复数，Pl，k(z)为一个次数不超过l-1的矩阵值多项式，Ql，k(z)为一个最多k次的数量多项式.注意到，只要 Ql，k(z1)≠0，可将Ql，k(z)规范化，使得Ql，k(z1)=c0=1.相比文献［4，7-8］中的GMRI法，式(4)中分母多项式的次数没有奇偶次限制.

定理1 假定zi互不相同.若Ql，k(zi)≠0，i=1，2，…，l，则式(4)中定义的矩阵值有理函数Rl，k满足如下的插值条件：

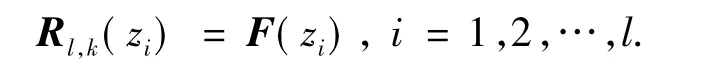
证明 由式(4)可得

令z=zi，由Lj+1，l(zi)=F(zi)，i=j+1，j+2，…，l以及W1，j(zi)=0，i=1，2，…，j，有

W1，j(z)［F(z)-Lj+1，l(z)］=0，i=1，2，…，l.定理得证.

2 误差公式及系数选择

由上节不难发现，式(4)中的ci是任意的.基于随后给出的引理3中的迭代关系，本节讨论怎样选取合适的cj来获得较好的逼近效果.首先介绍矩阵内积的通常定义.

令矩阵A=(ai，j)，B=(bi，j)∈Cs×t，定义A，B的内积为

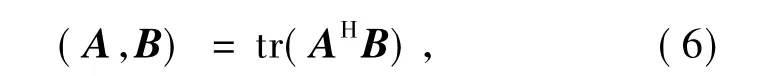
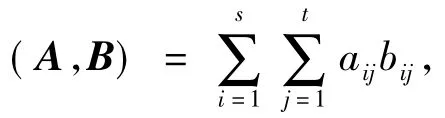
引理1 令A，B和C∈Cs×t，则

(b)任给α，β∈C，(αA+βB，C)=α(A，C)+ β(B，C);

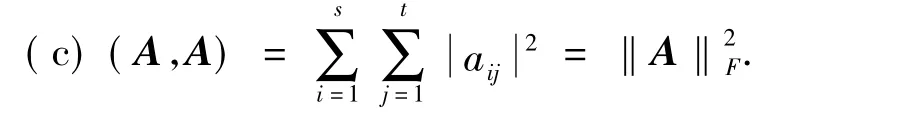
引理2［13］若 f(x)在包含着插值节点 z0，z1，…，zn的区间［a，b］上n+1次可微，则对任意z∈［a，b］，存在与x有关的ξ(a＜ξ＜b)，使得

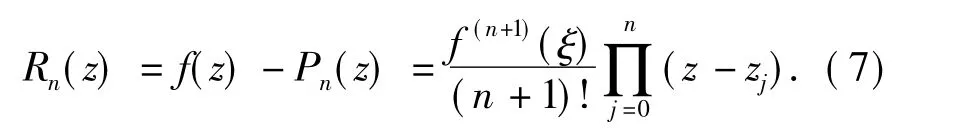
引理3 令Lm，n(z)为式(1)中定义的F(z)关于节点zm，zm+1，…，zn的矩阵值拉格朗日多项式，可得如下的迭代关系：

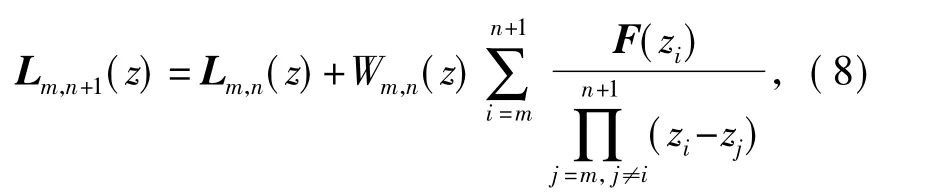
式中，Wm，n(z)由式(3)给出.

证明 由式(1)可得

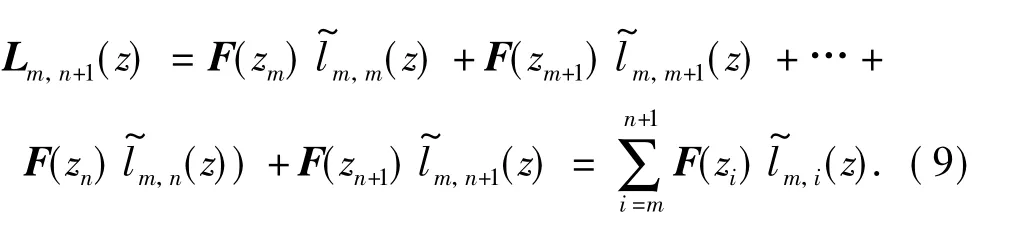
由式(1)和(9)可推出F(zi)的系数，即

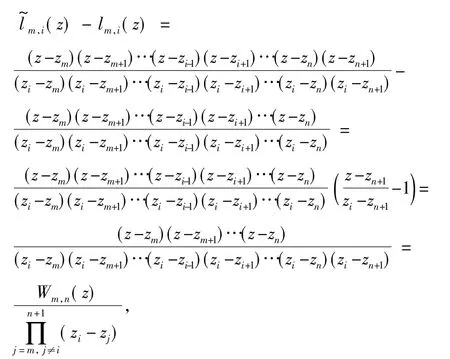
式中，m≤i≤n.式(8)得证.令

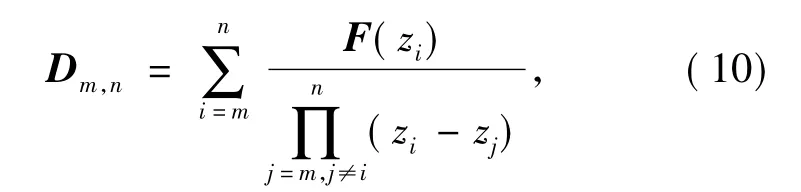
则式(8)变为

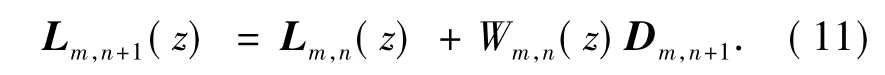
定理2 令z为一个复变量，F(z)为一个矩阵值函数F：C→Cs×t.若Rl，k(z)为式(4)给出的矩阵值有理函数，则

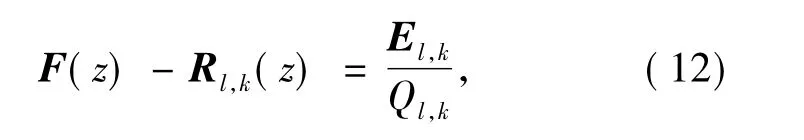
式中，

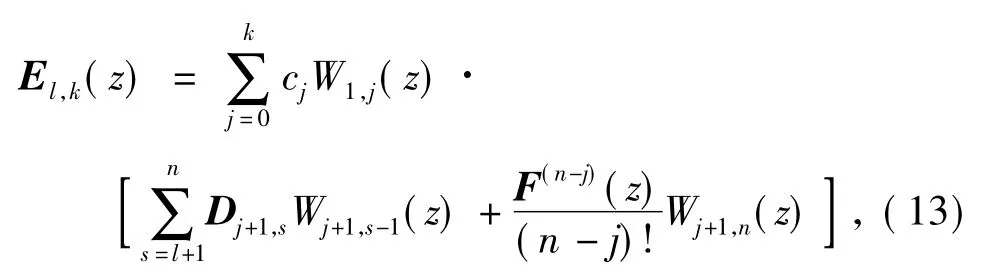
且Wm，n(z)，Dm，n分别由式(3)和(10)给出.

证明 由于Lm，n(z)为F(z)关于节点 zm，zm+1，…，zn的插值多项式，由式(8)可得误差公式为

令m=j+1，由引理3和式(11)，有

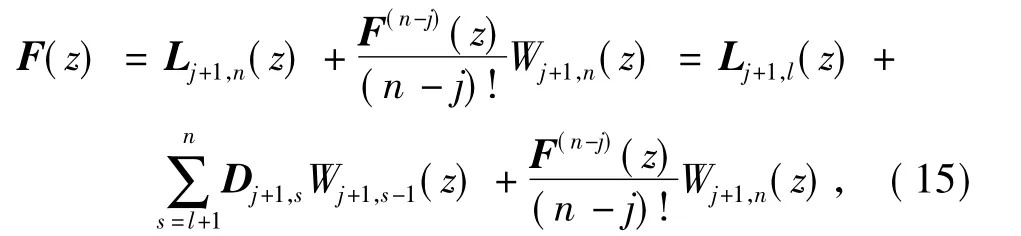
式中，0≤j≤k，n≥l.将式(15)代入式(5)，即可得到式(12).

根据式(3)，将式(13)改写为

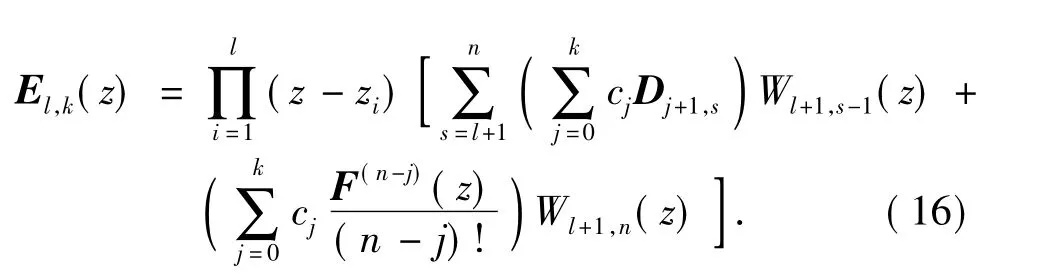
可以发现，式(16)方括号内的Di，j，i=1，2，…，k+1，j=l+1，l+2，…，n，可以重排为如下格式：

本研究通过3种不同的方法选取cj，使得式(16)方括号内的项在某种意义下尽可能的小.这里，对c0进行规范化，即c0=1.

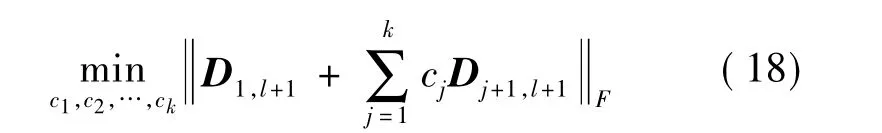
的解，其中假定 D2，l+1，D3，l+1，…，Dk+1，l+1为非零矩阵.于是将问题转化为F-范数下的最小二乘求解问题.事实上，式(18)等价于求解如下的线性系统：

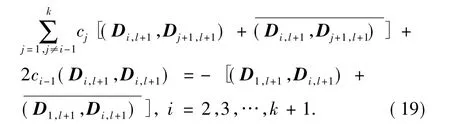
特别地，当Di，l+1∈Rs×t，i=1，2，…，k+1时，式(19)变为

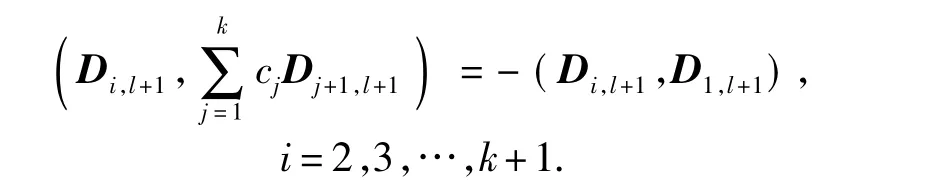
方法2 设矩阵D为D1，l+1，D2，l+1，…，Dk+1，l+1; D1，l+2，D2，l+2，…，Dk+1，l+2;…;D1，l+k，D2，l+k，…，Dk+1，l+k中的第一个非零矩阵，则通过求解下列线性系统来确定c1，c2，…，ck：

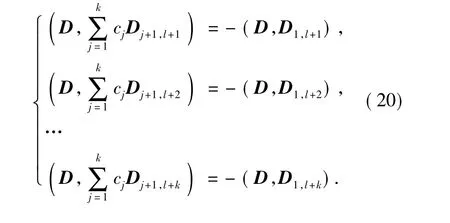
方法3 令式(16)中的c1，c2，…，ck为下列线性系统的解［12］：

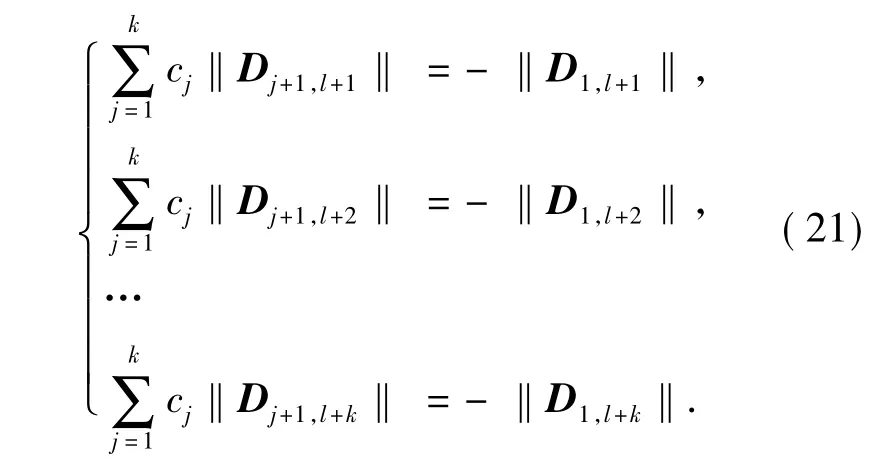
3 指定极点的有理插值式的插值节点选取原则

定义1 给定序列：

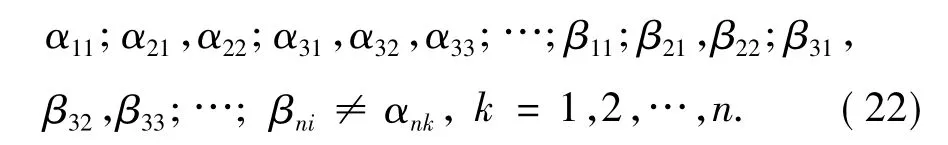
定义f(z)关于点βn1，βn2，…，βnn的插值函数序列为

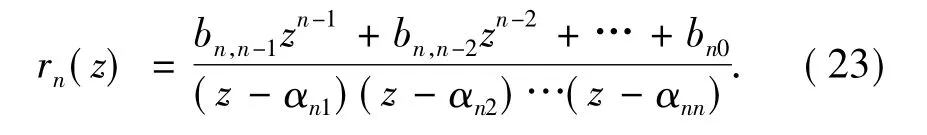
定义2［14］若Γ为中的闭Jordan曲线，则ext(Γ)为CΓ的包含C+的连通分支.

定义3［14］设 f(z)为 G⊃中的解析函数，Γ(∞∈Γ)={z：Re z=-a}(a＞0)为G∪{∞}中的可求长 Jordan曲线.其中为给定的多项式序列，其中αni∉{Re z≥-a}，βni∈且不同于αni.若

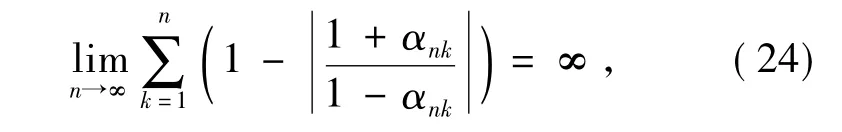
且

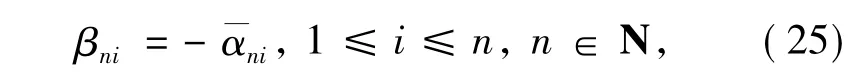
则指定极点的插值函数序列(rational interpolants with prescribed poles，RIPPs)rn(z)=Bn(z)/Qn(z)一致收敛到f(z).

基于插值公式(4)，给出逼近有指定极点的矩阵值函数的算法.假定F(z)为有指定极点的矩阵值函数，则第一步为计算F(z)的极点;第二步为利用式(25)确定插值节点，去除第一步中不重要的极点;第三步为利用插值式(4)逼近函数F(z).

例 考虑如下矩阵值有理函数的插值问题：

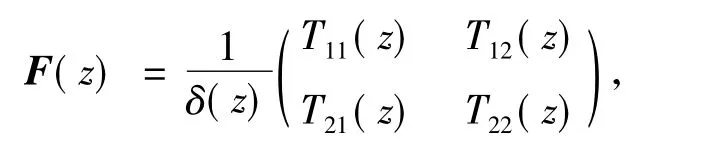
式中，

函数 F(z)的极点为 -0.243 747 876 5，-2.373 140 546，-27.890 485 68，-36.717 000 60，-48.848 388 70，-71.291 618 30+636.280 518 7i，-71.291 618 30-636.280 518 7i.

由式(25)，选取插值节点z1=0.243 747 876 5，z2= 2.373 140 546，z3= 27.890 485 68，z4= 36.717 000 60，z5=48.848 388 70.根据插值公式(4)，可得插值函数R4，3(z)为

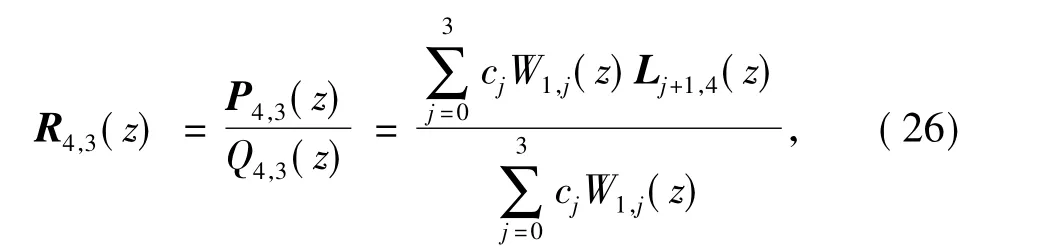
式中，

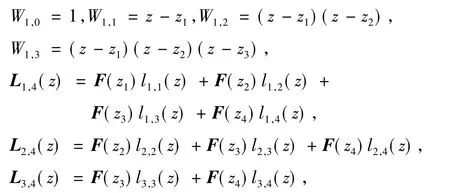
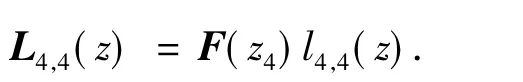
系数cj可由第3节介绍的3种方法求出，这里以方法1为例.由式(19)可得

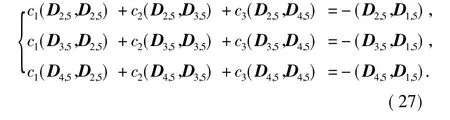
Dm，n由式(10)给出，即

由此，计算式(27)，有

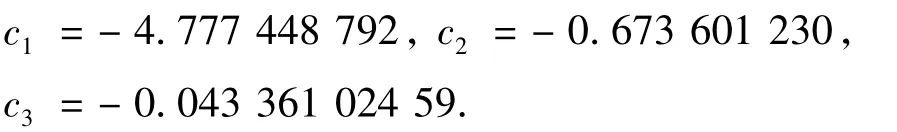
由于R4，3(z)和F(z)均为2阶矩阵，给出矩阵R4，3(z)中4个元素逼近函数F(z)相应元素的图形，如图1～图 4所示，其中实线为 R4，3(z)，点线为F(z).可以看出，在区间［1，∞)上，插值函数R4，3(z)能较好地逼近被插函数F(z).特别地，在区间［50，∞)上，两函数曲线误差极小，这表明本研究提出的算法是有效的.

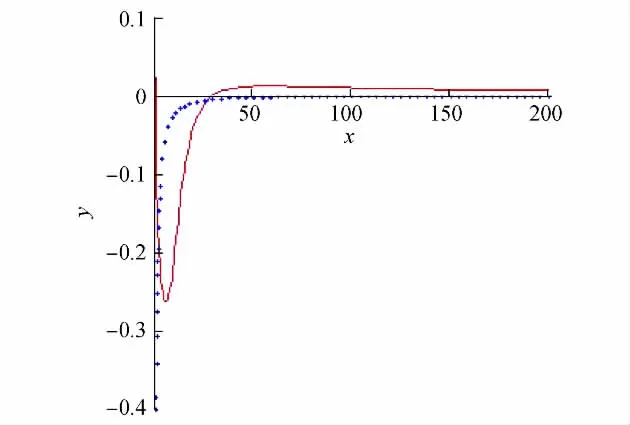
图1 R4，3(z)和F(z)的第一行第一列的元素Fig.1 Element［1，1］of matrices R4，3(z)and F(z)

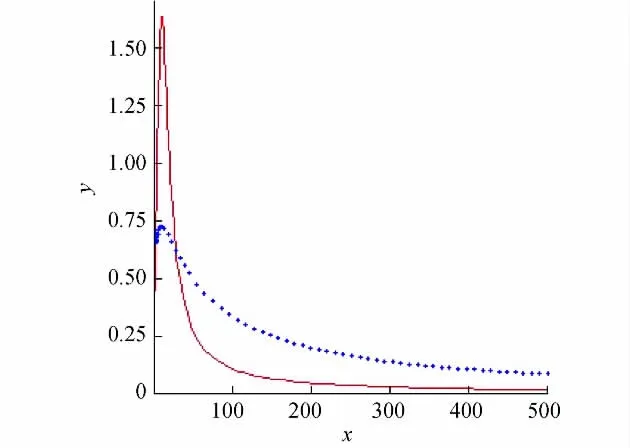
图2 R4，3(z)和F(z)的第一行第二列的元素Fig.2 Element［1，2］of matrices R4，3(z)and F(z)

图3 R4，3(z)和F(z)的第二行第一列的元素Fig.3 Element［2，1］of matrices R4，3(z)and F(z)

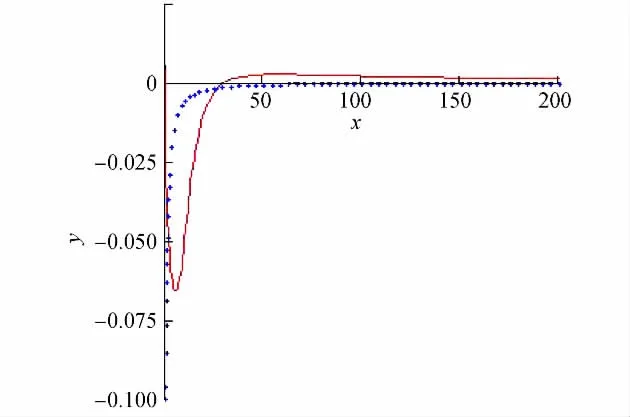
图4 R4，3(z)和F(z)的第二行第二列的元素Fig.4 Element［2，2］of matrices R4，3(z)and F(z)

［1］ BECKERMANNB，LABAHNG.Recursiveness in matrix rational interpolation problems［J］.J Comput Appl Math，1997，77(1/2)：5-34.

［2］ ANTOULASA C，BALLJ A，KANGJ，et al.On the solution of the minimal rational interpolation problem［J］.Linear Algebra Appl，1990，137：511-573.

［3］ ANDERSON B D O，ANTOULASA C.Rational interpolation and state-variable realizationas［J］.Linear Algebra Appl，1990，137：479-509.

［4］ GUC Q.Thiele-type and Lagrange-type generalized inverse rational interpolation for rectangular complex matrices［J］.Linear Algebra Appl，1999，295：7-30.

［5］ GRAVES-MORRIS P R. Vector valued rational interpolantsⅠ［J］.Numer Math，1983，42：331-348.

［6］ GRAVES-MORRISP R，JENKINSC D.Vector valued rational interpolantsⅢ［J］.Constr Approx，1986，2：263-289.

［7］ GUC Q.Generalized inverse matrix Padé approximation on the basis of scalar product［J］.Linear Algebra Appl，2001，322：141-167.

［8］ GUC Q.A practical two-dimensional thiele-type matrix Padé approximation［J］.IEEE Trans Automat Control，2003，48：2259-2263.

［9］ SIDIA.A new approach tovector-valued rational interpolation［J］.Journal of Approximation Theory，2004，130(2)：179-189.

［10］ SIDIA.Rational approximations from power series of vector-valued meromorphic functions［J］.Journal of Approximation Theory，1994，77(1)：89-111.

［11］ GUC Q.Matrix Padé-type approximant and directional matrix Padé approximant in the inner product space［J］.J Comput Appl Math，2004，164：365-385.

［12］ GUC Q，WU B B.Some practical determinants of matrix Padé-type method and computation of matrix exponential［J］.J Information and Computational Science，2005，2 (2)：243-250.

［13］ 王仁宏.数值逼近［M］.北京：高等教育出版社，1999.

［14］ STANFORDA R.Approximation of transfer functions of infinite dimensional dynamical systems by rationl interpolants with prescribed poles［J］.Journalof Mathematical Analysis and Applications，2000，244 (1)：147-168.