蚁群算法在作业调度中应用研究
朱福珍,朱凌
(扬州职业大学,江苏扬州225009)
作业调度主要研究如何合理配置加工过程的各种资源,减少零件的加工准备,从而提高设备利用率与生产效率,降低生产成本。蚁群算法是人类在长期观察蚁群觅食活动中总结出来的仿生优化算法。混流装配线是指在一定时间内,在一条生产线上生产出多种不同型号的产品,产品的品种可以随顾客需求的变化而变化。它是车间作业调度的具体应用之一。现以混流装配线为例,讨论蚁群算法在混流装配线作业调度上的应用。
1 蚁群算法简介
本文以汽车组装为例,即在组装所有车辆的过程中,所确定的组装顺序应使各零部件的使用速率均匀化。如果不同型号的汽车消耗零部件的种类大致相同,那么原问题可以简化为单级流装配线调度问题。由此,该问题可描述为[1]式中,i表示车型数的标号;n表示需要装配的车型数;m表示装配线上需要的零部件种类总数;p表示生产调度中子装配的标号;αp表示零部件p的理想使用速率;j表示车型调度结果(即排序位置)的标号;D表示在一个生产循环中需要组装的各种车型的总和;di表示在一个生产循环中车型i的数量;bip表示生产每辆i车型需要零部件p的数量;βj-1,p表示在组装线调度中前j-1台车消耗零部件p的数量和βj-1,p+xjiβip,且β0,p=0。

2 算法的具体应用
这里采用如图1所示的搜索空间定义,列表示排序阶段(用j表示),行表示每个阶段可供选择的车型(用i表示),圆圈的大小表示选择概率的大小,蚁群算法就是不断改变圆圈的大小,最终寻找到满意的可行解。这里假设有3种车型A、B、C排序,每个生产循环需要A型车3辆、B型车2辆、C型车1辆,则每个循环共需生产6辆车(D=6)。列表示6个排序阶段,行表示有3种车型可以选择。图1(a)是搜索的初始状态,圆圈由局部搜索值和信息素综合而成;图1(b)经过若干次迭代之后,搜索空间变化,此时最可能的可行解[2]是B-A-C-A-B-A。

图1 简单混流装配线排序的搜索空间举例
利用这种表示方法可以降低问题描述的维数,其问题规模为O(n,m),其中n是车型数,m是排序长度。
2.1 局部搜索(ηij)的计算
计算公式如下
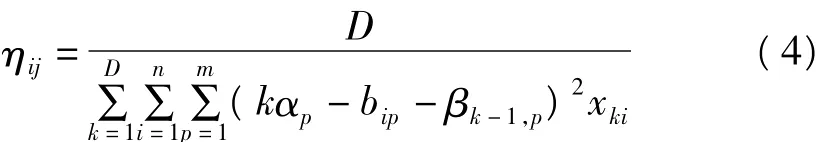
局部搜索ηij采用的是贪婪法。[3]目标追随法的思路是,每一步均从当前可选择策略中选取,使目标函数值增加最少的策略,即在确定第n+1台车辆车型时,如果有多种车型可供选择,则从中选择一种车型,使第n+1台车辆组装时各零部件使用速率最为均匀。若每步只考虑当前的状态,而不考虑全局状态,这样得到的结果常常为局部最优解。但是蚁群算法为每个可选择的车型i计算ηij,最后再结合信息素的作用对车型做出选择。
2.2 状态转移概率
状态转移概率公式如下

2.3 信息素更新规则

式中,LB表示目标函数的下限值;Z表示当前目标函数的平均值;Zcutr表示当前的目标函数值。[4]这种动态标记的方法可在搜索过程中加大可行解间信息素的差别,避免算法早熟,见图2。

图2 线性动态标注

3 算例分析
算例数据来源于扬州亚星客车股份有限公司的生产数据,该公司主要生产各种车型的客车,数据见表1。
对参数设置经过多种组合实验,得到蚁群算法最优组合参数为ρ=0.9,α=0.2,Q=20000,Ncmax=400,n=5目标函数值为2859.8。排序结果为C-A-D-E-B-A-D-E-A-C-A-B-E-D-A-C。
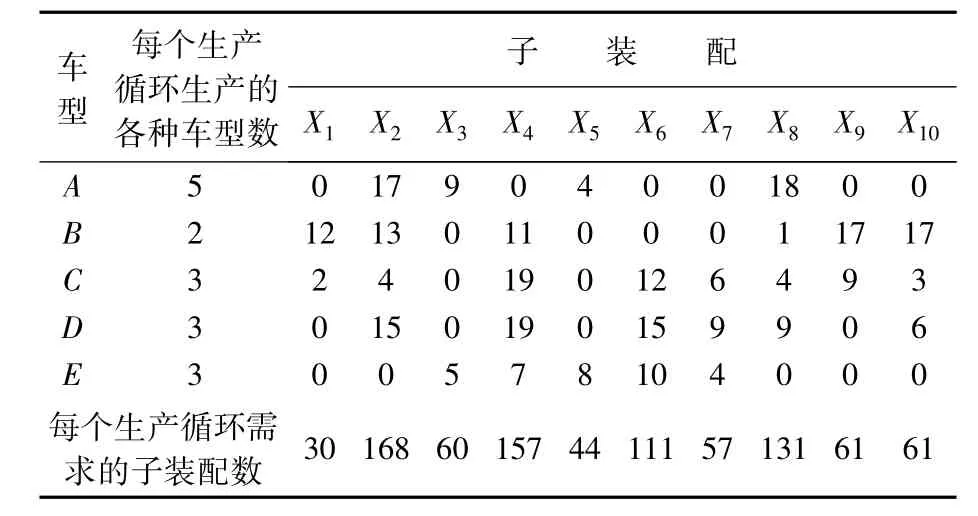
表1 各车型的物料单和需求的子装配数
用蚁群算法进行反复实验,并同时与目标追随法、遗传算法和模拟退火算法相比较,结果见表2。
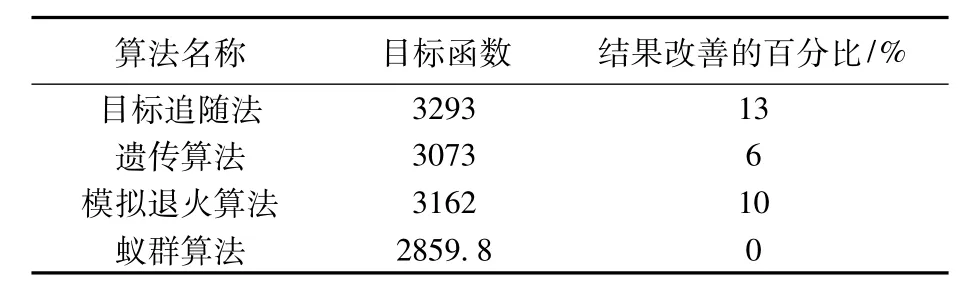
表2 蚁群算法与其他启发式算法的对比
由表2可见,蚁群算法的求解性能优于其他启发式算法。
4 结论
本文采用局部搜索、状态转移概率、信息素更新规则分析了蚁群算法在扬州亚星股份有限公司生产的某种车型混流装配线调度上的具体应用,结果证明跟其它算法相比,它有较优的加工路径。
[1]GAO Q L,LUO X,YANG S Z.Stigmergic cooperation mechanism for shop floor control system[J].International Journal of Advanced Manufacturing Technology,2009,25(7):743-753.
[2]王常青,操云甫,戴国忠.用双向收敛蚁群算法解作业车间调度问题[J].计算机集成制造系统,2009,7(10):820-824.
[3]刘海龙,郑春,黄小源.Job shop的多机多目标调度[J].系统工程理论方法应用,2007,5(2):68-72.
[4]周国华.生产作业调度的软计算方法研究[J].系统仿真学报,2008,8(2):24-35.

