带时间窗口的任务可分活动网络协作计划模型

王芳芳，包振强，丁泉勋，汪 成，张惠秋

（扬州大学 信息工程学院，江苏 扬州 225127）

在生产过程中，由于生产资源、生产时间、技术等多种因素的限制，生产部门接到的生产任务有时不可能全部完成，须要将生产任务的一部分外包给供应链上的其他协作伙伴，于是产生了协作计划.目前，对协作计划优化问题的研究虽有很大进展，但多数协作计划模型中协作资源的开工时间被视为确定的值，并且任务不可分.［1］事实上，在实际应用中存在着许多不确定因素，协作资源在任务请求的计划周期内给出的开工时间往往不是一个确定时间，而是提供一个时间窗口［2］；而且在实际协作生产中，有一部分任务是可以任意拆分的，而另外的部分任务却是有条件拆分的［3］.为此，本文针对上述问题，提出基于时间窗口的任务可拆分协作计划模型，采用合同网的协作机制［4］，解决时间窗口约束下任务可拆分的协作计划问题，以降低协作成本；另外，结合粒子群算法［5］在求解连续性最优化问题方面的优势和遗传算法的选择、变异机制，设计了求解该模型的进化算法.

1 协作计划模型

协作计划问题可进行如下描述：在由多个有时序关系的任务构成项目中，每个任务可由一个执行部门或多个执行部门合作完成，每个部门以已知执行时间区域及给定的资源需求为特征，当本部门所能支配的资源不足以完成当前的计划任务集时，如何选择各任务的完成模式以及安排各活动的开始时间，使得活动网络的时间资源消耗最少和总成本最低.对协作计划模型作如下简化假设：协作任务不容许转包；协作者对协作任务的报价与任务招投标顺序无关；假设资源需求在任务使用范围内为均匀分布模式以及单位时间内任务对资源的需求为常数；系统有足够多的协作资源，异地资源具有相同的效用.

上述问题可表述为下列规划模型.

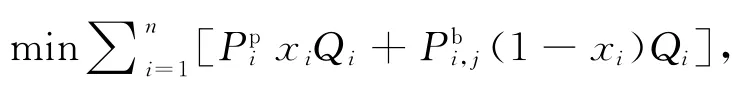
在协作计划系统项目中，假定任务集为J.设Qi为任务ji的生产量；为任务ji单件产品最低的竞标价格；为任务ji单件产品的计划价格；xi为本部门自己加工任务ji的百分比；ti为任务ji的外协部门执行时间；是本部门执行任务ji的单件成本；是外协部门m执行任务ji的单件成本.

模型约束条件如下：

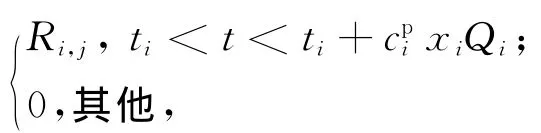
4）总工期约束.max｛Fj≤T｝.

在协作系统项目计划中，假定产生竞标方案的任务集为J.设Qi为任务ji的生产量；为计划期内能提供的自有资源的加工能力；Ri，j为任务ji的单件产品对j类资源的能力需求；为任务ji生产单件产品最低的竞标价格；为任务ji生产单件产品的计划价格；xi为本部门自己加工任务ji的百分比；ti为任务ji的外协部门执行时间；是任务ji的外协部门m 最早执行时间；是任务ji的外协部门m最迟执行时间；T表示项目的交货期；ti是任务ji本部门的执行时间；是任务ji本部门的最早执行时间；是任务ji本部门的最迟执行时间；Fi是任务ji的结束时间是本部门执行任务ji的单件成本；是外协部门m执行任务ji的单件成本.

2 基于协作模型的混合粒子群算法

2.1 适应度函数和选择机制

协作计划模型中时间和成本是不同量纲的参数［6］.为此，将时间先进行无量纲的标准化处理，再根据对时间和成本的要求分别确定其加权系数.将多目标函数转化成单目标函数.无量纲标准化量化的公式如下：

根据时间和成本的要求确定权系数w＝（w1，w2）利用线性加权的综合，

本文选用比例计算生存概率，即pi＝fi／∑fi，采用轮盘赌［7］进行选择.

2.2 算法设计

1）初始化算子.在初始化范围内对粒子群进行随机初始化，产生m个n维向量.向量的维数n与活动网的活动个数相同；m作为这个种群的大小，在迭代过程中不变，同时随机地产生初始位置和速度.初始化的粒子尽可能覆盖整个解空间［8］.

2）约束条件的处理.本文采用惩罚函数法，设置统一的惩罚项常数H.

3）惯性权重［9］.一个由m个粒子组成的群体在n维搜索空间中以一定的速度飞行，每个粒子搜索时，在考虑到自己搜索的历史最好点和群体内其他粒子搜索的历史最好点的基础上进行位置的变化.粒子的位置和速度根据下列方程进行变换：

式中w是惯性权重.带惯性权重的粒子群算法是基本粒子群算法的扩展.

4）选择操作.本研究中引用轮盘赌方法计算个体的选择概率，产生新种群.采用精英保存策略，当种群数量减少时，随机生成粒子补充种群数量.

5）变异操作.粒子群算法的收敛速度较快，但容易选入局部最优［10］.本文通过变异操作，对粒子群算法进行改进，使其具有更好的全局性.设置最大速度vmax，当向量速度v的各维中含有大于或等于1的分量时，使用如下公式进行变异操作：

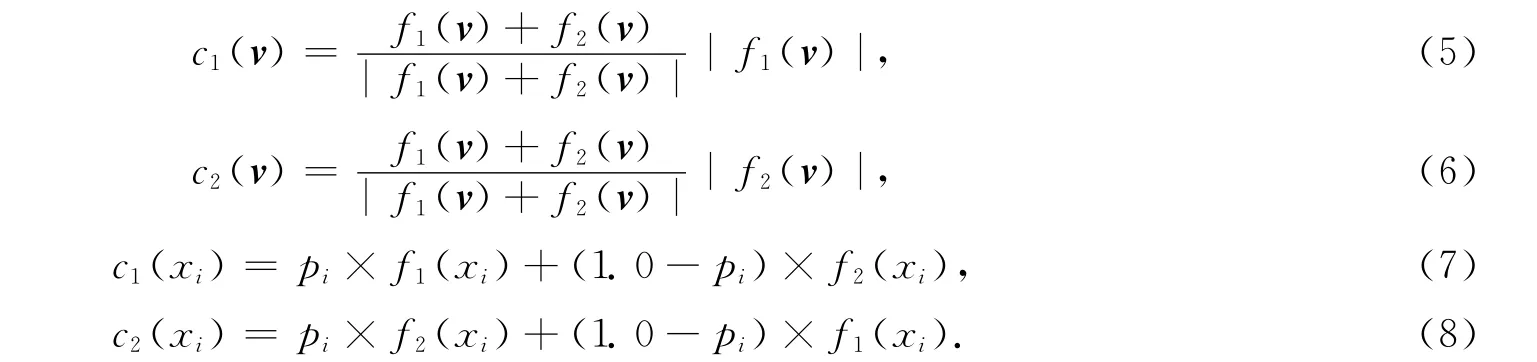
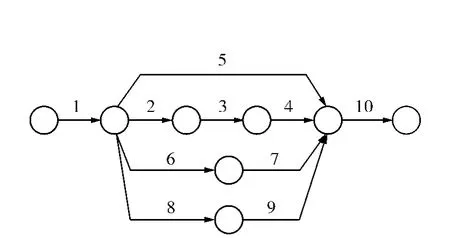
图1 计划任务的网络图Fig.1 Active network fig

3 算例仿真

设项目部共有10项任务活动.图1为计划任务的网络图，其中任务10不对外招标，与生产任务相关的自有资源共5种，它们在计划期内的能力数据及各任务对各种能力的需求（按单位产品计）列于表1中，各生产任务的生产量也在表1中列出.

将这10项任务分别向协作伙伴招标.10项任务中有9项在规定的时间内产生竞标方案，J10没有产生竞标方案为第i个任务的最低竞标价，设置各参数如表2中所示，招标中获得的数据也列于表2中.

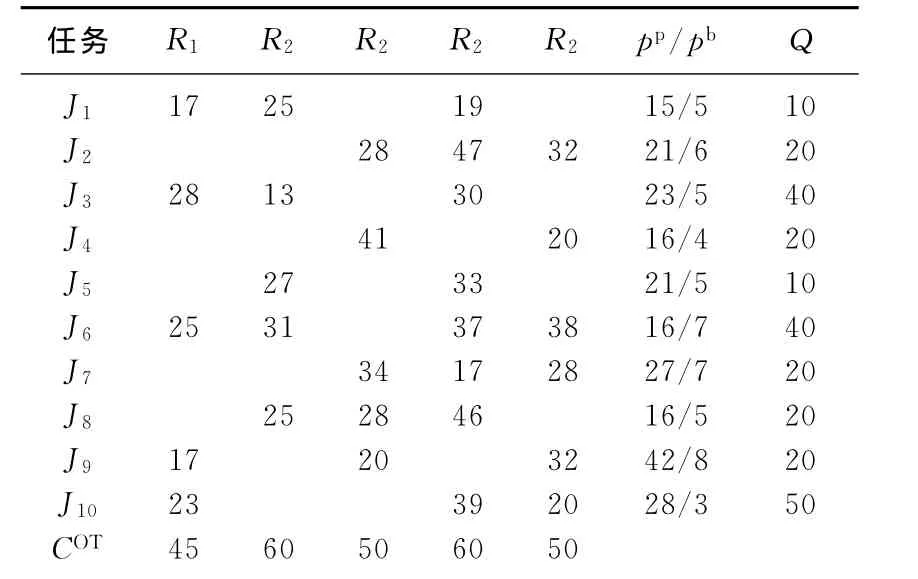
表1 计划期的任务数据与相关约束资源Tab.1 Task data and constraint resource in planning period

粒子群算法的运行参数设定如下：群大小为50，变异概率为0.1，Fi，j表示第i项任务外包给第j个服务提供者，终止代数为1 000，采用WIN－TC编写程序.算法程序运行显示，随着群体的进化，目标函数以较快的速度收敛，反复运行程序均具有稳定的解.

运行算法程序，得到不同权重条件下的最优结果，见表3.

4 结语

协作计划优化是供应链优化的一个重要组成部分.本文建立了一个带时间窗口的任务可分的活动网络协作计划模型.该模型使得企业在完善内部资源优化的前提下能够更加有效地衔接外部资源，协作计划具有更大优化空间，供应链更加灵活.带时间窗口的约束解决了任务的开工和结束时间具有不确定性的问题，从而更加符合实际生产的需求.同时，本文采用能够优化连续问题的粒子群算法，结合遗传算法的选择、变异机制，建立了相应的仿真软件，通过算例进行仿真运算，证明该模型及其求解算法是可行且有效的.

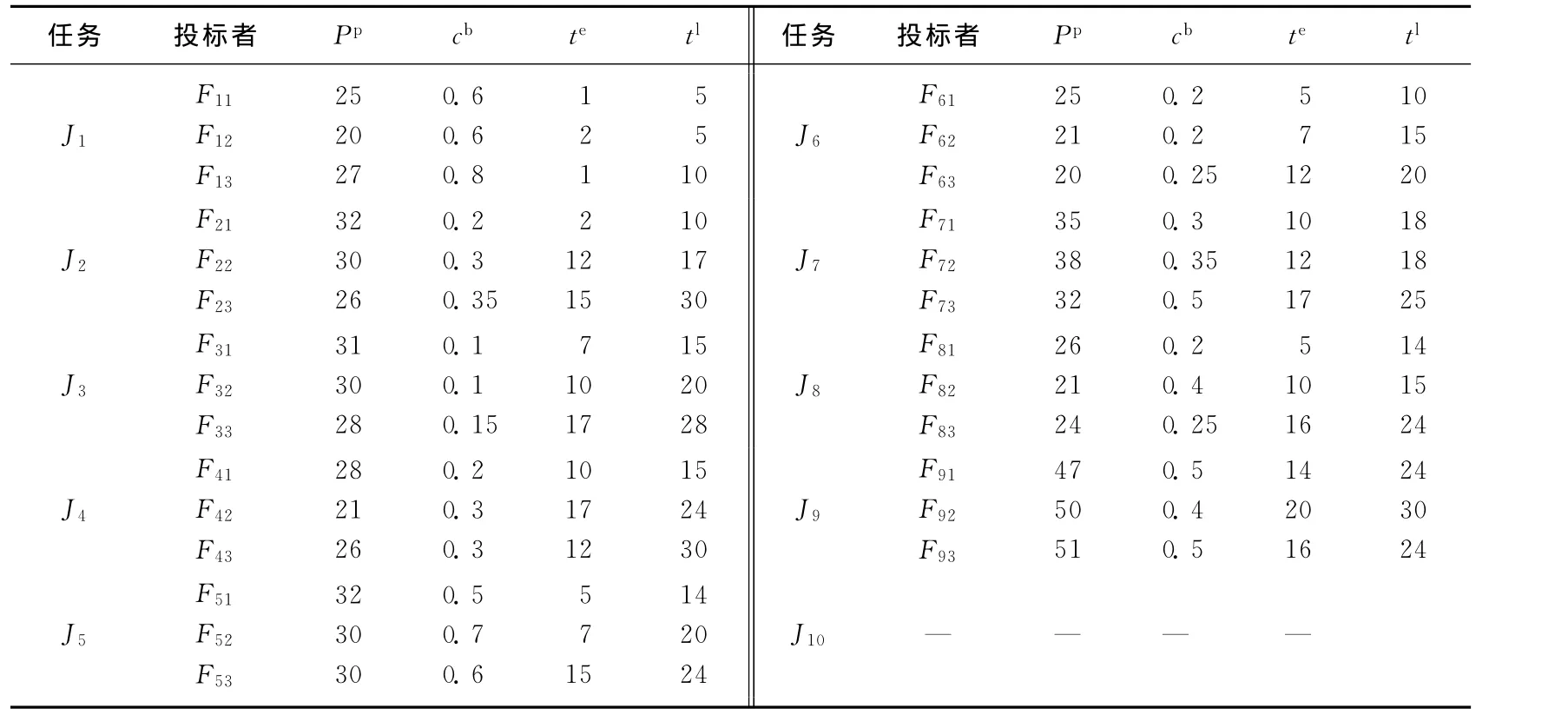
表2 由招投标过程获得的数据Tab.2 The data of inviting and entering bids

表3 不同权重下的协作计划及指标Tab.3 Object and results of cooperation planning in differentweight

［1］SHAO Zhi－fang，ZHANG Tao.Study on hierarchy collaborative planning for TFT－LCD production chain［C］／／The 1st International Conference on Information Science and Engineering.Nanjing：ICISE，2009：3069－3072.

［2］衣杨，李强，容福丽，等.时间窗口约束资源配置的混合粒子群算法 ［J］.计算机研究与发展，2008，45（增刊）：233－238.

［3］ZHANG Jian－feng，ZHOU Lei，BAO Zhen－qiang，et al.A cooperation－planning model based on bilevel programming decision［J］.Jwuhan Univ Tech，2006，28（s3）：940－945.

［4］LAI H F，HONG J L，JENGw H.Model E－contract update by coloured activity net［C］／／Asia－Pacific Services Computing Conference.Yilan，Taiwan：APSCC，2008：488－493.

［5］黄少荣.粒子群优化算法综述 ［J］.计算机工程与设计，2009，30（8）：1977－1980.

［6］张雪霞，陈维荣，戴朝华.带局部搜索的动态多群体自适应差分进化算法及函数优化 ［J］.电子学报，2010，38（8）：1825－1830.

［7］王芳，邱玉辉.一种引入轮盘赌选择算子的混合粒子群算法 ［J］.西南师范大学学报：自然科学版，2006，31（3）：93－96.

［8］GUOw Z，GAO F.Solution space atlases，workspace characteristics charts and joint space maps for the design of planar serial manipulators［J］.Mech Mach Theory，2010，45（3）：392－407.

［9］MO Lin，ZHENG Hua.Improved PSO algorithm with adaptive inertia weight and mutation［C］／／World Congress on Computer Science and Information Engineering.Los Angeles，California，USA：CSIE，2009，4：622－625.

［10］RATNAWEERA A，HALGAMUGE S K，WATSON H C.Self－organizing hierarchical particle swarm optimizer with time－varying acceleration coefficients［J］.IEEE Trans Evol Comput，2004，8（3）：240－255.