用并联补偿解耦法设计MIMO控制的仿真

黄 威，夏 洪，张秀喜，尧 征，郑振峰

（东华理工大学 机械与电子工程学院，江西 抚州 330013）

1 引言

各个控制通道中的耦合广泛存在于多输入多输出(MIMO)的系统当中，并且时滞现象往往会影响单输入对单输出(SISO)的稳定性和控制的特性。对于实际成产过程当中，往往多个变量相互关联，一个输出受多个输入的控制，一个输入控制多个输出，并且各个控制通道存在不同程度的滞后，这样解耦补偿矩阵成为了解决滞后现象的关键。传统解决这一问题的方法主要有：前馈补偿解耦、反馈补偿解耦、对角矩阵解耦，但是对角矩阵补偿法（Diagonal Matrix Decoupling method，DMD）是广泛应用的解耦方法。但从一些资料上看来，在用这种方法计算耦合项的函数项时，都把延时项去掉，这样大大简化计算的复杂性。而在实际的工程应用过程中，如果将延时项去掉的话，控制的稳定性和系统的特性将大大缩小。

假设有图1所示的2输入2输出耦合系统，X1通K21g21过对X2管道有耦合作用，表达式为：

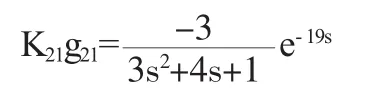
X2通过对X1产生耦合作用其表达式为：

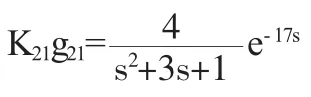
X1通道的被控制量的表达式为：

X2通道的被控制量的表达式为：

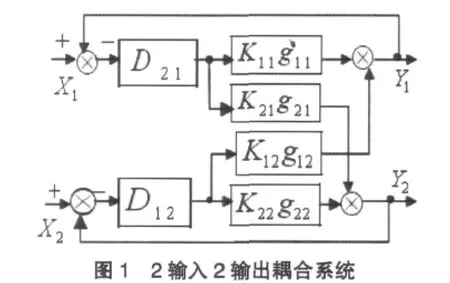
X1，R（s），K和Y1共同构成通道，通常采用预估器和解耦器，控制器为回路的控制图，如图 2 所示，R（s），Y（s）表示系统输入，输出变量，G（s）为被控时滞对象，K（s）表示解耦器，C（s）表示控制器。H（s）不包含时滞部分。

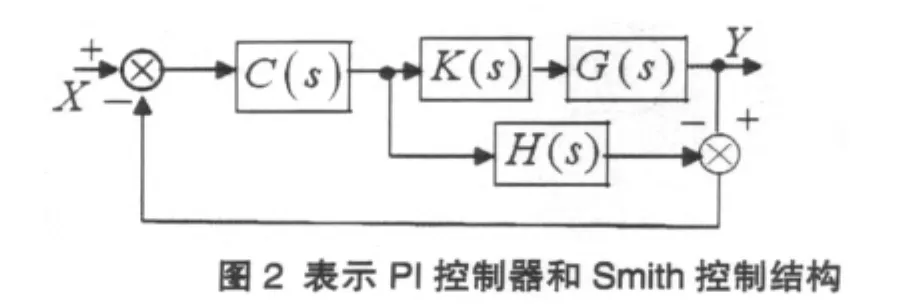
图 3 中 C（s）为 PI控制器，K（s）)G（s）)为被控制对象的传递函数，先假设二个通道相互独立，用Simulink软件仿真，仿真图如4所示，其中C（s）的参数,积分系数Sp1为27，比例系数Si1为0.2.第二个通道Sp2为8，Si2为0.8.Input1值为3的阶跃信号，Input2值为2的阶跃信号。

PI为控制器，其内部的 Si1，为 0.2，Sp1为 27。

最后得出的仿真结果稳定性比较好。如图5所示。

2 并联补偿法(PCD)设计

在工业自控系统中的2输入2输出系统中，由于系统多个通路之间存在着相互耦合，并且当系统的复杂性增大以后，传统的解耦方法并不能十分有效地解决这个问题，所以本文利用一种新的方法——并联补偿法，在耦合项加上一项大小相同但方向相反的耦合项，使得耦合项的作用大大减小。

该 仿 真 实 验 时 间 分 别 为 t=200，400，600，800，1000，2000，8000，10000，20000s，在仿真之后，比较并联补偿法与对角解耦法的优势。

3 结论

本文使用了一种新的解耦方法，从上面的例子可以看出，并联解耦比对角解耦的要求的条件更低，而且稳定性能更好。对角矩阵要求受控对象的矩阵必须是可逆的，但是并联解耦矩阵却没有这方面的要求。显示出了并联解耦法的优点。

[1]金以慧，方崇慧.过程控制[M].北京：清华大学出版社，1993.

[2]谢任宏.MATALAB R2008控制系统动态仿真实例[M].北京：化学工业出版社，2009.

[3]翁怡方.自动控制理论[M].北京：机械工业出版社出版，2007.

[4]刘豹.现代控制理论[M].北京：机械工业出版社，1992.