三维各向异性铁磁系统的自旋波谱及基态能量

成泰民， 葛崇员， 祁 烁

(沈阳化工大学数理系，辽宁沈阳110142)

因为体系的任意幺正变换关联着同一个量子体系的不同表象之间的变换，所以蕴含着该量子体系的严格一致的物理内容，这些幺正变换对该量子体系的描述是完全等价的.因此，在磁性物理及量子力学中普遍采用不同的幺正变换处理系统哈密顿量的对角化，求出元激发能量及基态能量.但是这一方法的关键是做出适合体系对角化的不同的幺正变换，最终把体系哈密顿量表示成对角化形式［1－2］.

对于三维各向异性铁磁性系统而言，磁晶各向异性的基态性质较复杂，且又涉及到其激发态与其元激发能量和基态能量密切相关，并且此种材料的输运性质及多体相互作用下的重正化的元激发性质、谱线宽度、元激发的寿命、系统的配分函数、磁化强度、磁化率、热性质等都与铁磁性晶体材料的自旋波谱(磁振子谱)及其基态能量的特性及Hamiltonian的对角化密切相关［3－10］.为此，本文利用宇称变换和量子光学中的压缩变换对系统的Hamiltonian进行了对角化.这种处理方法物理思想清晰易掌握.

1 系统的Hamiltonian

局域电子模型下的各向异性Heisenberg铁磁性交换作用Hamiltonian如下:

其中J为铁磁交换积分，X1、X2、X3为各向异性参数，g为朗德因子，μB为玻尔磁子，H为外加磁场强度.

对(2)式进行逆变换:

(3)式的二次量子化处理利用了 D-M 变换［5，7－10］，具体如下:

其中N为单位体积内磁性离子或原子的个数(即粒子数密度).

把(4)式、(5)式代入到(3)式，并只取算符的二次项为止，可得:

其中

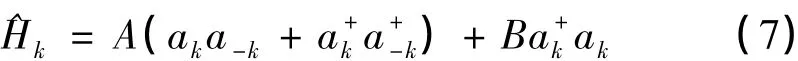
(7)式中A与B为:

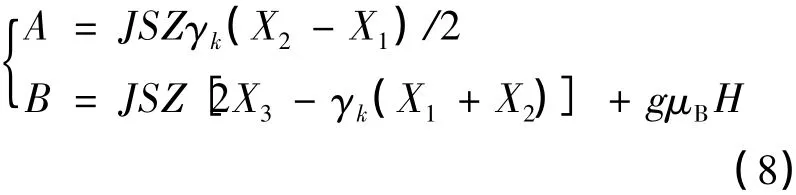
2 系统的Hamiltonian的对角化

2.1 宇称变换［1］

因为

所以有:

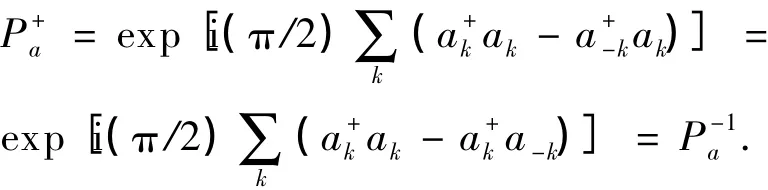
因此，宇称变换算符是幺正算符.

对(7)式进行(9)式的宇称变换，并考虑Hamiltonian的厄米性可得:

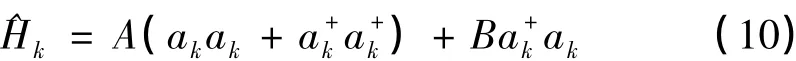
其中算符ak、a+k满足玻色子对易关系.

2.2 压缩变换(Squeezed transformation)［2］

为了消除(10)式中的A(akak+a+ka+k)耦合项，进行压缩变换［2］:

因为由(11)可得:

所以S(ξ)是幺正算符.

对算符ak、进行压缩变换:

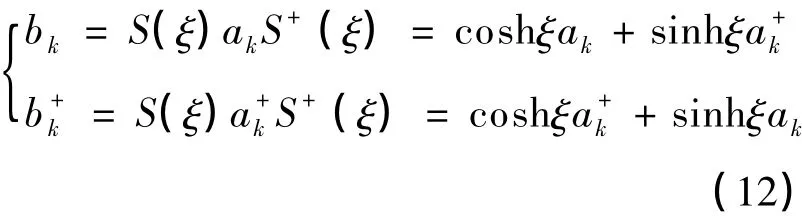
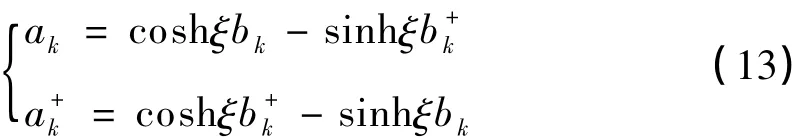
其中算符bk、也满足玻色子对易关系.把(13)式代入到(10)式可得:

因(11)～(14)式中ξ是任意值，所以令ξ=ξ1时满足:

(bkbk+)前的耦合项系数可以去掉，使 ^Hk成为对角化:

(12)式的逆变换:

其中

求解方程(15)式后，代入(17)式、(18)式，并由(8)式可得:

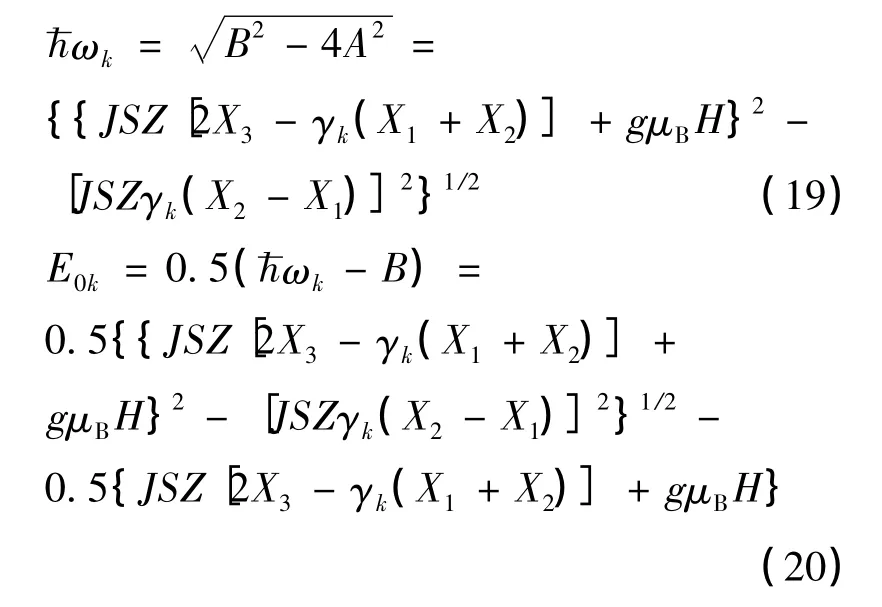
系统的基态能量为

3 讨论

当X2=X1时，代入(19)～(21)式可得XXZ-Heisenberg铁磁系统的自旋波谱及基态能量:

由(24)式可知XXZ-Heisenberg铁磁系统基态能量是常量.

当X3=X2=X1=1时，代入(19)～(21)

式可得各向同性铁磁系统的自旋波谱及基态能量:

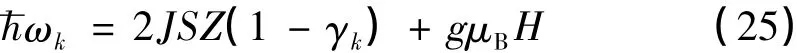
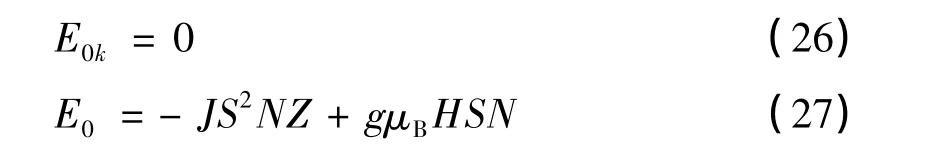
(25)～(26)式的结果与文献［11］的结果一致.

［1］ 何兵，应和平，季达人.X-Y-Z非各向同性反铁磁Heisenberg系统的自旋波解［J］.物理学报，1996，45(3):522－527.

［2］ Yuen H P.Two-photon Coherent States of the Radiation Field［J］Phys.Rev.A，1976，13(6):2226－2243.

［3］ 宛德福，马兴龙.磁性物理学［M］.北京:电子工业出版社，1999:149－152.

［4］ Aharoni A.铁磁性理论导论［M］.杨正，译.兰州:兰州大学出版社，2007:26－93.

［5］ Dyson F J.General Theory of Spin-wave Interactions［J］.Phys.Rev.，1956，102(5):1217－1230.

［6］ Cheng Taimin，Li Lin.Magnon-phonon Couplingin Two-dimensional HeisenbergFerromagnetic System［J］.J.Magn.Magn.Mater.，2008，320(1/2):1－7.

［7］ Cheng Taimin，Li Lin，Shen Longhai.Effect of Magnon LA Phonon Interaction on LA Phonon Excitation at Finite Temperature［J］.Phys.stat.sol.(b)，2008，245(4):673－677.

［8］ 成泰民，罗宏超，李林.有限温度下光频支声子-磁振子相互作用对磁振子寿命的影响［J］.物理学报，2008，57(10):6531－6539.

［9］ Cheng Taimin，Li Lin，Xianyu Ze.Effect of Magnon-phonon Interaction on Phonon Damping of Two-dimensional Heisenberg Ferromagnetic System at Finite Temperature［J］.Solid State Commun.，2007，141(2):89－94.

［10］Cheng Taimin，Li Lin，Xianyu Ze.Magnon Damping in Two-dimensional Heisenberg Ferromagnetic System［J］.Phys.Lett.A，2006，353(5):431－438.

［11］李正中.固体理论［M］.北京:高等教育出版社，2002:67－70.