基于迭代分形法的大气波前仿真

冯 麓

(中国科学院国家天文台，北京 100012;欧洲南方天文台自适应光学部，慕尼黑 加兴 85748)

1 背景

近年来，随着天文研究对望远镜光学成像系统分辨率的要求越来越高，望远镜的口径也不断增大。对于天文望远镜来说，天体和望远镜之间总存在着时时变化的大气，如果将其看作一面透镜，它复杂的运动方式意味着这面透镜的不同部分在不同时刻其折射系数是不同的。当无穷远处的天体发出的球面波前可以近似为平面波前并即将穿过大气时，大气会对穿透大气的波前幅度和相位造成影响，进而影响入射到望远镜的波前(图1)。这种非平面波前使望远镜因光学长度不同，而无法完美对焦，从而使得成像分辨率降低。

对于理想光学系统，光学分辨率λ同望远镜等效口径D有如下简单关系:

将大气视作整个光学系统中的一面透镜，可以找到一个相应的量r0来描述其等效口径，称为大气的相干长度。该度量的大小与大气波动的剧烈程度成反比。对于大口径望远镜来说，如果口径大于当地大气的相干长度，望远镜的光学分辨率将从(1)口径所决定的分辨率下降到由相干长度决定的分辨率，

通常认为，大气对入射波前相位的改变比幅度的改变对最终成像质量的影响更大［1］。也就是说，可以将大气的传递函数简化为:

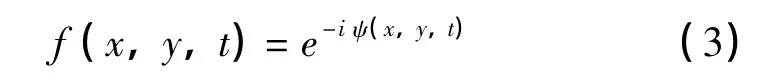
式中，ψ(x，y，t)通常被称作相位屏，它将一定高度内的大气对入射波前的影响简化作一层仅对波前相位做出改变的透镜。如果仿真出这个相位屏，就能仿真出大气对波前的影响，从而对后续光学系统设计和评估提供一个工具。

图1 无穷远处星光的球面波前在到达大气湍流时已可以近似为平面波前。在穿过大气时，这部分波前还将进一步被大气湍流所影响，变为曲面波前，进而影响后续光学系统成像Fig.1 Spherical wavefront of light from a star can be treated as planar.When passing through the atmosphere，the wavefront is distorted by turbulences，which affects the image quality of an observing telescope

迭代分形法的思想最早出现于文［2］，当时的目的是利用随机中点插值仿真一维布朗运动。文［3］则提出了二维相对Kolmogorov功率谱密度的迭代分形法，其基本思路同本文一致。文［4］对文［3］的方法进行改正，使得相应的k算子满足所有线性条件，但在该文中，目的是利用该算子进行波前重构，而非仿真。文［5］则对重构算法提出了进一步速度和并行化的改进，并对波前重构光学性能进行了评估。本文主要就k算子在波前仿真方面进行介绍，并给出在Kolmogorov功率谱密度模型下的仿真结果同理论结果的比较。

2 大气相位屏仿真

2.1 经典算法

通常在仿真相位屏时，首先认为大气符合Taylor Frozen Flow假设，即，

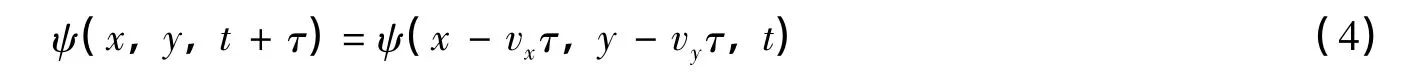
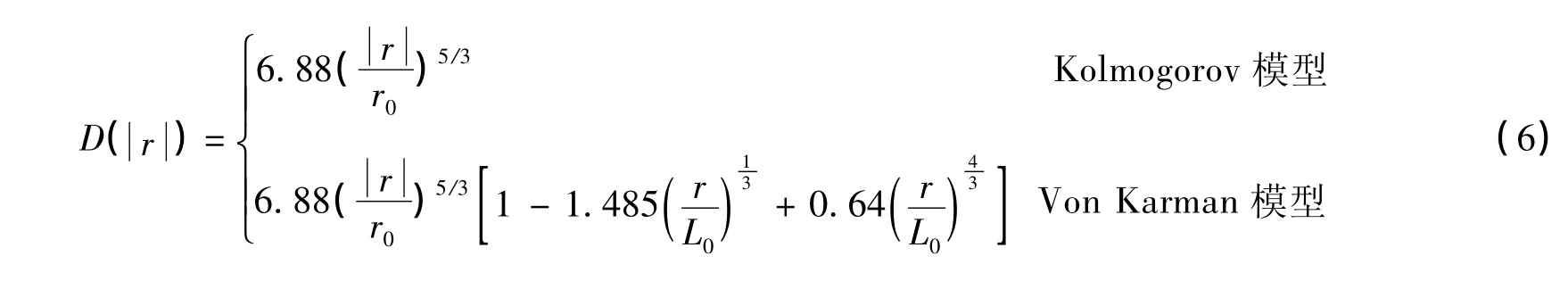
本文中，这两种模型都可以使用。

定义相位屏如图2，大气在有限空间上的演变可以由图2上的有限点取值的随机变化反应。对随机变化的任意两点间的相关函数为:

因为Taylor Frozen Flow假设认为同层大气随机运动各向同性，所以有:

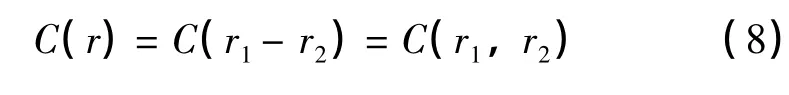
展开(5)式，并将(8)式代入，可得:

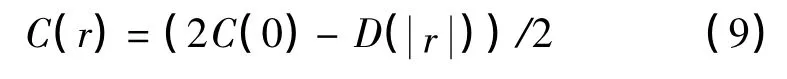
根据变形定理，对于符合任意分布的随机噪声均可以通过对白噪声的线性变换得到。换言之，随机变化的波前也可以通过线性算子对白噪声的变化得到:

式中，k为需要求得的线性算子;u为方差等于1的白噪声，代入(7)式有:

通常的相位屏仿真方法大致可以分为基于相关函数的各种分解模态分解算法和基于功率谱密度再作傅里叶变换的算法。后者的困难在于当仿真Kolmogorov相位屏时，Kolmogorov能量谱函数无限逼近于0，在0频时并不连续［6］，使得当计算频率逼近0点的低频值时不得不采用平滑或者0阶保持的方法得到这部分的功率谱。而基于相关函数分解的方法则不存在这样的问题。对于基于相关函数的计算方法，一种是通过直接计算(9)式得到相关矩阵，再利用奇异值分解得到:

由(11)、(12)式，可得:

通过上式，在计算得到k=U·S1/2后，便可以不断利用伪随机白噪声生成相应r0下的随机相位屏。另一种方法是利用Zernike基对相关矩阵进行分解，同样可以得到类似于(13)式的基展开矩阵同向量积的形式［8］。

尽管这类方法在计算得到k之后，整个方法简化为(13)式。但即使如此，因要计算矩阵矢量乘，计算复杂度仍然达到O(N2)，其中N为所有结点个数。同时尽管k可以反复使用，但(12)式计算复杂度在O(N3)的奇异值分解一步使得在进行对大相位屏或是对不同r0仿真时，计算时间过长。

2.2 迭代分形法:

该算法的主要依据是(7)式。以5×5结点相位屏为例(图3)，首先需要的是计算4个角的节点值(结点1～4)，然后利用这4个结点，进而向中间插值。对于这4个间距定义为D的结点，它们应该满足(7)式定义的相关条件，将其展开如下，并代入(9)式:

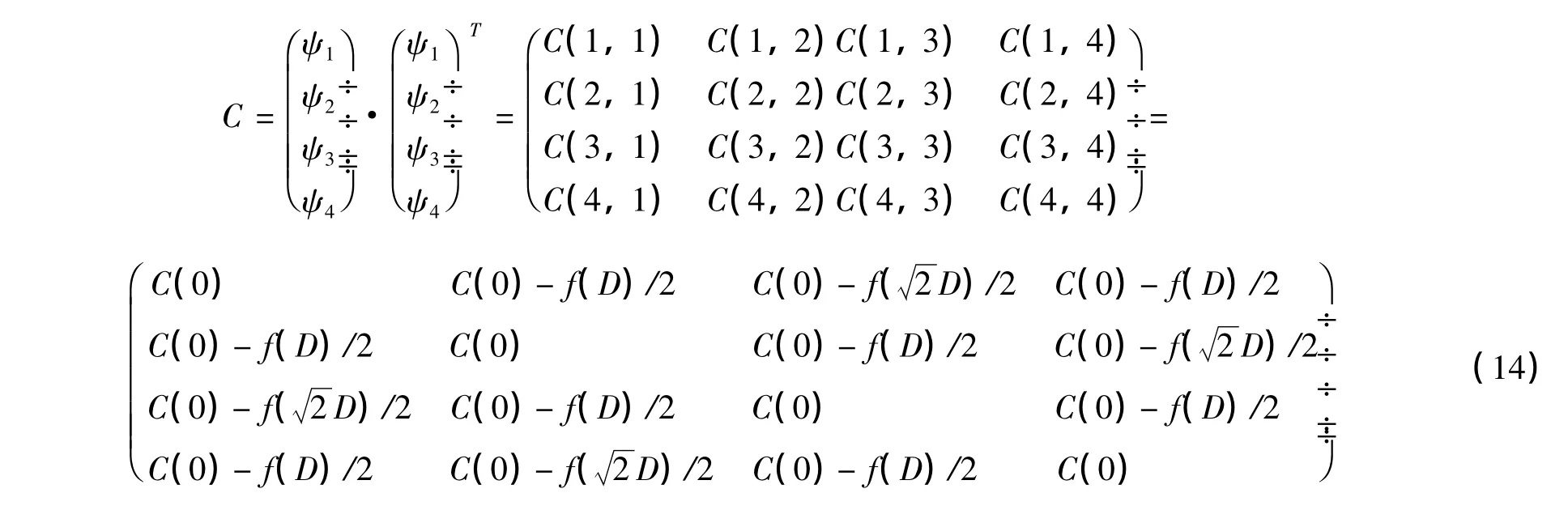
对(14)式同样可以依照(11)式进行分解，文［4］给出了其分解形式如下:

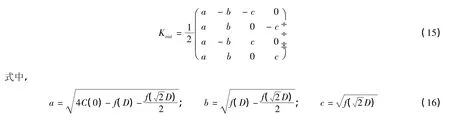
利用(15)、(16)式以及(10)式便可得到符合Kolmogorov模型的角落4个结点的值。这里C(0)的值对于Kolmogorov模型来说，可以作为自由度处理，对于Von Karman模型，因其引入外尺度系数，C(0)将取决于外尺度系数同相关尺度系数。

以角落4个结点的值为起点，就可以不断利用随机中点插值将该尺度的其余点一一计算出来，然后将同样的插值过程应用到下一个尺度的所有未被计算到的结点，重复该过程直到遍历所有节点。其中值得注意的有两点，一是插值存在对遍历顺序的要求［4］，二是因为利用的是中点插值，所以对相位屏结点个数存在限制，即每边结点个数应为N=2i+1，其中i为自然数。

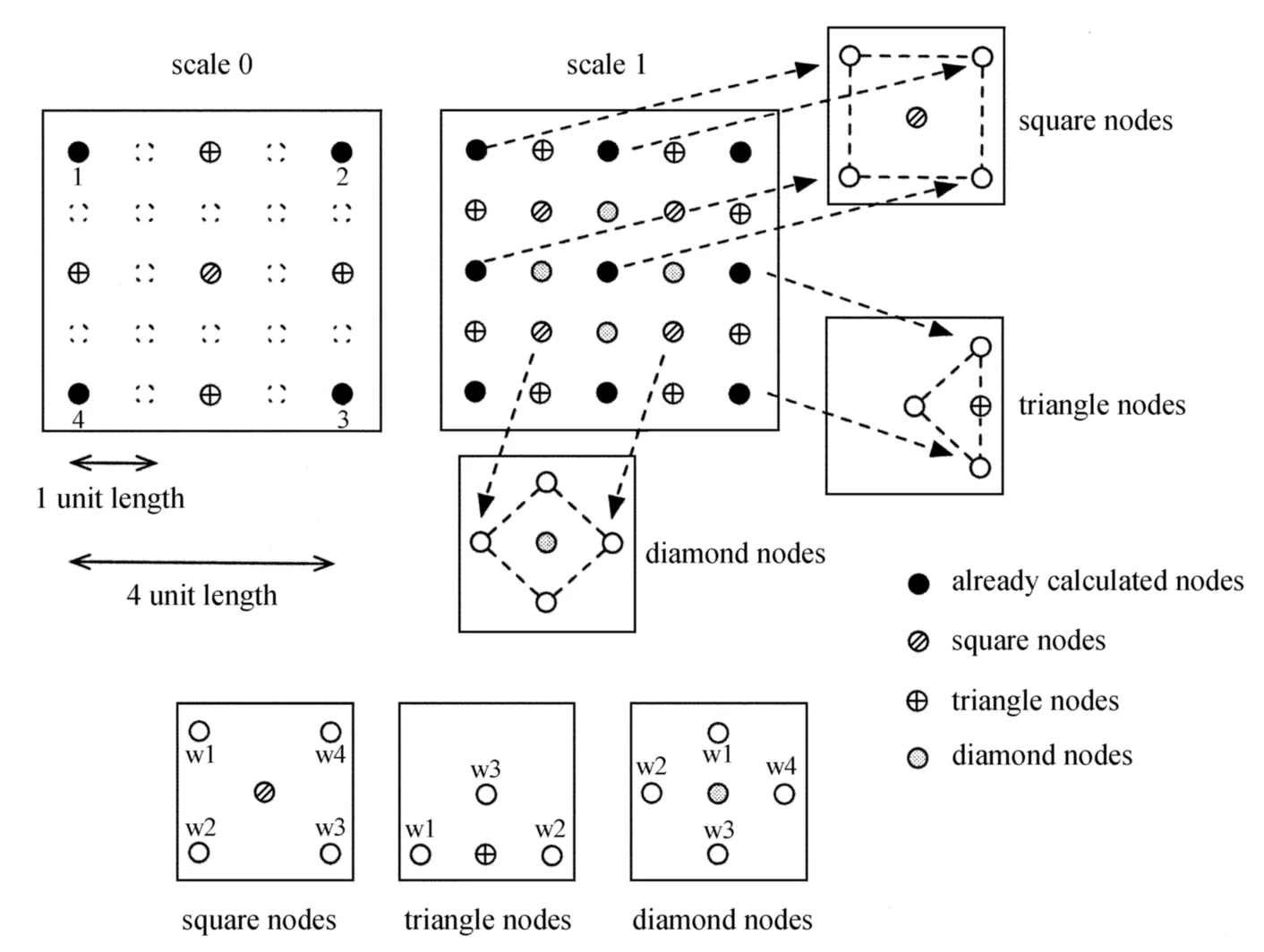
图3 迭代分形法算子，该计算可以分解成4步，计算初始角落4点，然后根据节点位置进行迭代。颜色点在迭代过程当中为欲求结点w0Fig.3 Calculation for the operator k involves 4 steps as follows:initial calculation for the corner elements and subsequent calculations of inner elements on three fractal types of nodes.Calculations are carried out iteratively by alternating the types of nodes until all nodes are calculated.In the bottom row of the plot，a colored node w0 is the node to be calculated

随机中点插值法的理论思想是在若干结点已知的情况下，当未知结点同已知结点保持简单中心几何关系的前提下，且相关函数可推，则利用该推导公式，便可以确定下式的权重系数:

式中，当已知结点在正方形4角，欲求为中心，称这个结点为正方形结点，当欲求结点在相位屏边界时，所处位置为已知3个结点中心，称这个结点为三角形结点，当欲求在两个共边正方形公共边上时，称为菱形结点。

这里的推导方法同推导Kout是相同的。利用(17)和(15)式，并假设〈w20〉=C(0)，可以得到相关函数和权重系数之间的关系如下:

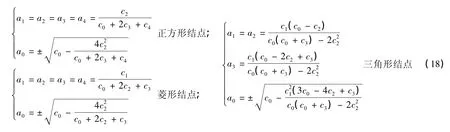
式中，±对结果没有影响，参数定义如下:

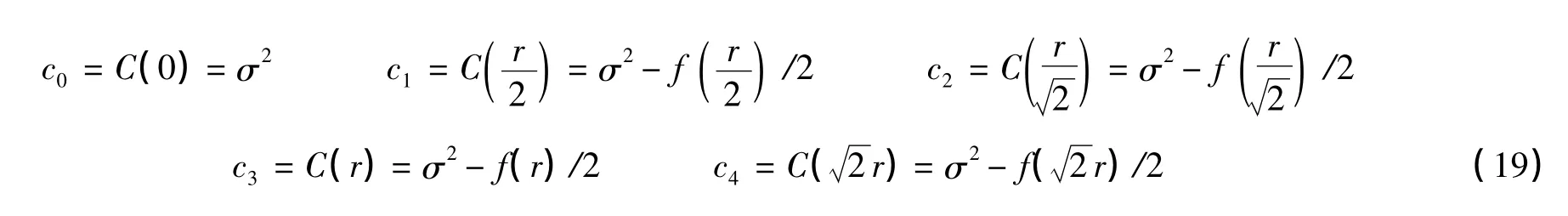
对于实际计算过程，所有系数都可以根据(18)、(19)式提前计算得出，且计算量远远小于对相关矩阵的计算。在生成相位屏时，整个迭代过程可以视作遍历所有点，且遍历过程中的计算仅需访问固定邻近不大于4个点，所以整个过程的复杂度仅仅为O(N)。存储空间也因为涉及计算只是本地值更新，所以仅需N个浮点数加少量浮点数表征权重值。

图4 分形迭代法仿真数据得到的相位屏结构函数与理论Kolmogorov结构函数的差别Fig.4 Phase-screen structure function from the FriM method as compared to the theoretical Kolmogorov model

3 结论

图4给出利用该方法仿真Kolmogorov大气模型的相位屏的结构函数及其理论值。参考文［3，6，10－11］，本算法所得相位屏，统计特性与大气模型吻合程度与其他经典算法基本相同，且不会出现基于功率谱函数不存在而引入的拟合误差［10］，所以在理论上不逊色于其他算法。同时因省却了大型相关矩阵的运算以及其他基于矩阵矢量乘的算法，有效提高了算法的运算速度。且如上节所述，该算法对内存空间要求远低于需要存储N阶模态值的算法。鉴于此认为该算法对仿真大相位屏或者需要快速仿真的应用是有所帮助的。

致谢:感谢欧洲南方天文台E Fedrigo，A Glindemann，C Béchet对本文工作的大力帮助。

［1］John W Hardy，Laird Thompson.Adaptive Optics for Astronomical Telescope［M］.Cambridge:Cambridge University Press，1999.

［2］Heinz-Otto Peitgen，Dietmar Saupe.The Science of Fractal Images［M］.New York:Springer Verlag，1988.

［3］R G Lane，A Glindemann，J C Dainty.Simulation of a Kolmogorov Phase Screen ［J］.Waves Random Media，1992，2(3):209－224.

［4］Eric Thiébaut，Michel Tallon.Fast Minimum Variance Wavefront Reconstruction for Extremely Large Telescopes［J］.Journal of the Optical Society of America A，2010，27(5):1046－1059.

［5］Montilla C Béchet，M Le Louarm，M Reyes，et al.Performance Comparison of Wavefront Reconstruction and Control Algorithms for Extremely Large Telescope ［J］.Journal of the Optical Society of America A，2010，27(11):9－18.

［6］Michael C Roggemann，Byron Welsh.Imaging through Turbulence ［M］.CRC Press，1996.

［7］Rober L Lucke，Cynthia Y Young.Theoretical Wave Structure Function When the Effect of the Outer Scale is Significant［J］.Applied Optics，2007，46(4):559－569.

［8］熊耀恒，白金明.应用自适应光学望远镜所取得的天文观测成果 ［J］.云南天文台台刊，2000(2):48－57.Xiong Yaoheng， Bai Jinming. Astronomical Observation Results Using Adaptive Optical Telescopes ［J］.Publications of the Yunnan Observatory，2000(2):48－57.

［9］周钰，熊耀恒.基于自然导引星的自适应光学系统非等晕性分析 ［J］.天文研究与技术——国家天文台台刊，2009，6(1):8－12.Zhou Yu，Xiong Yaoheng.Analysis of Anisoplanatic Errors in Adaptive Optical Systems Based on Natural Guiding Stars ［J］.Astronomical Research ＆ Technology——Publications of National Astronomical Observatories of China，2009，6(1):8－12.

［10］C M Harding，R A Johnston，R G Lane.Fast Simulation of a Kolmogorov Phase Screen ［J］.Applied Optics，1999，38(11):2161－2170.

［11］Robert K Tyson.Finite Outer Scale Zernike Polynomial Phase Screen Generator［C］//Adaptive Optics for Large Telescopes Topical Meeting，1992:22－24.