天文成像数值仿真的相位屏模拟方法*

常 翔，李荣旺，熊耀恒

(中国科学院国家天文台/云南天文台，云南 昆明 650011)

天文成像是光通过湍流大气传播成像的过程。在弱起伏湍流情况下折射率随机起伏引起的相位变化φ足够小，可以将湍流大气这样的连续随机介质分割为一系列厚度为Δzs的传播平面，在该薄屏上加入相位调制，即为薄相位屏［1－2］。薄相位屏是分析弱湍流下光传播的基础，也是天文成像理论的重要内容。对于通常的天文成像，即目标光线沿垂直路径传播的情况，一般用简单的统计模型描述沿光传播路径上的介质，即把大气划分为由有限数目的离散层组成。这种近似既有数学上的简单性，也更符合实际大气情况。在弱起伏湍流前提下，数值仿真的有效性就取决于仿真中所设置的大气层次模型是否与湍流介质折射率起伏统计性质相符［3］。这主要体现在两个方面:首先，模拟生成的相位屏是否准确反应了相应折射率随机起伏的统计特性;其次，由多相位屏组成的大气层次模型是否准确反映了所要模拟的大气湍流模型特征。前者主要取决于相位屏模拟方法的使用，后者则由传播路径上相位屏的分布决定。

本文首先介绍了常用的相位屏模拟方法，并对方法的准确性和有效性进行验证分析。然后结合天文观测给出多相位屏的湍流分层模型。最后设计了基于部分相干光成像的天文成像过程进行数值仿真实验，并给出仿真结果。

1 相位屏模拟及验证

基于傅里叶变换的谱反演相位屏生成法，最初由B L McGlamery提出［4］。假设湍流影响下的相位是一组傅里叶变换序列，可以表示为傅里叶积分的形式:

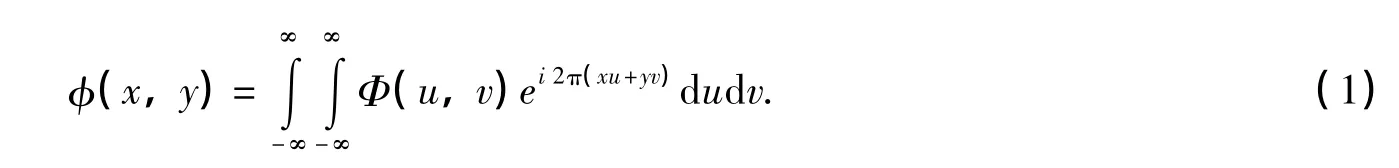
式中，Φ(u，v)是作为一个随机过程的相位空间频谱形式。相位功率谱密度Φφ(κ)等效的二维形式Φφ(f)对其进行滤波处理就可以得到符合湍流统计性质的相位功率谱密度。此处给出文中用到的Kolmogorov谱和修正 von Kármán 谱的相位功率谱［2］:

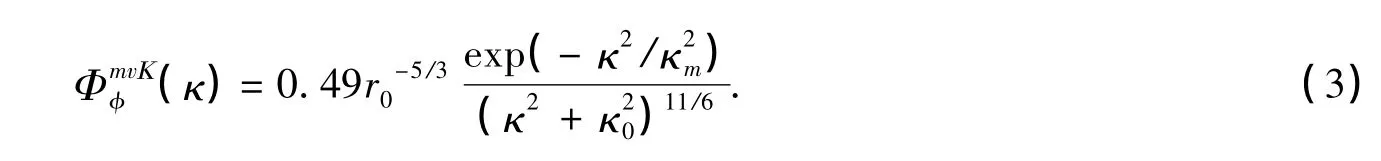
式中，0≤κ≤∞为空间波数，且有κm=5.92/l0，κ0=2π/L0分别对应湍流内尺度l0和外尺度L0。

由Parseval定理有相位与功率谱密度的关系:

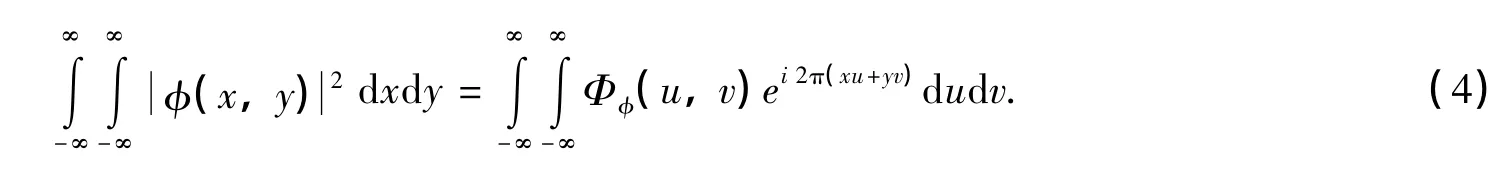
然后利用傅里叶逆变换就可以得到一个独立的随机相位屏。

在数值仿真中，为生成一个有限采样网格的相位屏，将相位写为一组傅里叶序列的形式［5－6］:

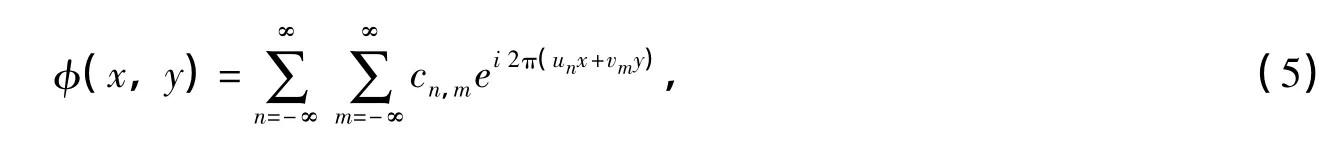
式中，cn，m为傅里叶序列系数;un、vm是离散化的空间频域坐标。弱起伏湍流扰动相位服从高斯分布，因此系数cn，m也为正态分布。更确切地说，(5)式中的相位应服从圆型复高斯分布，实部和虚部均值为零，方差相等，且互协方差为零［1］。由此，系数cn，m的方差为:

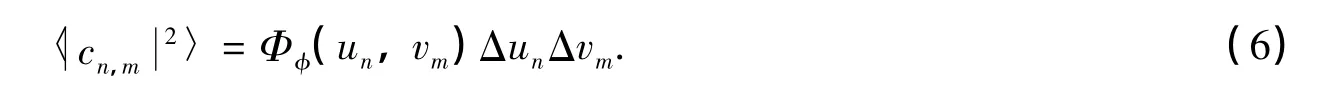
在计算中使用FFT算法，采样间隔由采样网格大小定义。设x、y方向上的采样网格大小分别为Lx、Ly，则有采样间隔Δun=1/Lx、Δvm=1/Ly。上式就简化为:

现有很多软件和程序都可以生成高斯随机数。设生成的高斯随机变量x均值为μ，方差为σ2。则通过z=(x－μ)/σ这一简单的变换，就可以得到需要的零均值、等方差高斯随机数。然后利用(6)式得到系数cn，m，由(5)式就得到数值模拟的随机相位屏。

尽管上述方法效率很高，但生成的相位屏却有不准确的缺点。由于大气折射率起伏的功率谱密度在低频部分较高，相应地，相位的能量也多集中在低频部分。而上述的谱反演相位屏生成法却由于有限的空间采样，无法准确描述波前起伏的低阶模式。很多文献都提出了针对这个缺陷的改进和补偿。本文使用的方法是由R G Lane最先提出，通过非等间隔采样加入低频补偿的一类次谐低频补偿方法(SH－FFT)［5－7］。

在利用谱反演法生成的相位屏基础上，由Np个相位屏叠加得到的“次谐”(Sub－harmonic)低频补偿相位屏:

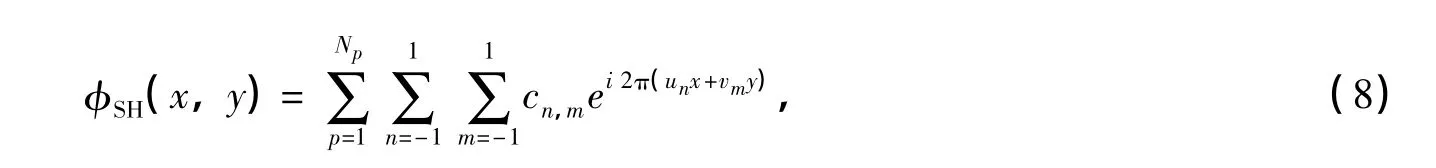
式中，每个序数p代表的次谐相位屏对应不同的采样网格。在本文的模拟中，对使用3×3的网格划分次谐相位屏，共有Np=3个不同采样网格使用。每个次谐网格对应的频率采样间隔为Δfp=1/(3pL)，L为谱反演生成的相位屏网格大小。

图1给出了数值方法模拟生成的随机相位屏。模拟使用(2)式给出的Kolmogorov相位功率谱密度，并设定r0=0.1 m，采样网格大小为512，相位屏尺寸为4 m，可明显看出低频补偿的区别。

用上述相位屏生成方法，本文利用Monte－Carlo方法对相位屏模拟结果进行分析。图2为使用Kolmogrov相位功率谱模拟得到的相位屏相位结构函数对比，分别为线性视图和对数视图。通过40个随机相位屏样本结构函数的系综平均进行比较，分别给出了使用前文所述SH－FFT方法、直接谱反演法，以及65阶Zernike多项式模拟得到的结果。从图2(b)可以看出，谱反演一类方法在高频部分与理论值较为相符，而Zernike多项式方法模拟到65阶仍然与理论值偏离较大;而在图2(a)中尽管直接谱反演得到的结果低频不足，但经过次谐补偿后的结果在r/r0=10时的结果与Zernike多项式方法得到的结果已经等同。而Zernike多项式法的相位屏模拟，由于其系数间的相关性，无法直接用随机数生成来模拟，还需通过将其系数相关矩阵分解，转换为系统统计独立的K－L模式进行随机相位屏生成，计算开销很大，效率不高。尽管计算到高于200阶时也能在高频部分与理论值符合较好，但对于需要大量统计样本的Monte－Carlo方法不适用。Zernike多项式的相位屏模拟方法可参考文［8－9］，本文不再详述。

图1 相位屏数值模拟结果示意图(a)、图(b)分别为次谐低频补偿和直接谱反演法得到的相位屏单个样本Fig.1 Example of phase－screen simulation results.The frames(a)and(b)are the results with the SH－FFT method and the FFT method，respectively.

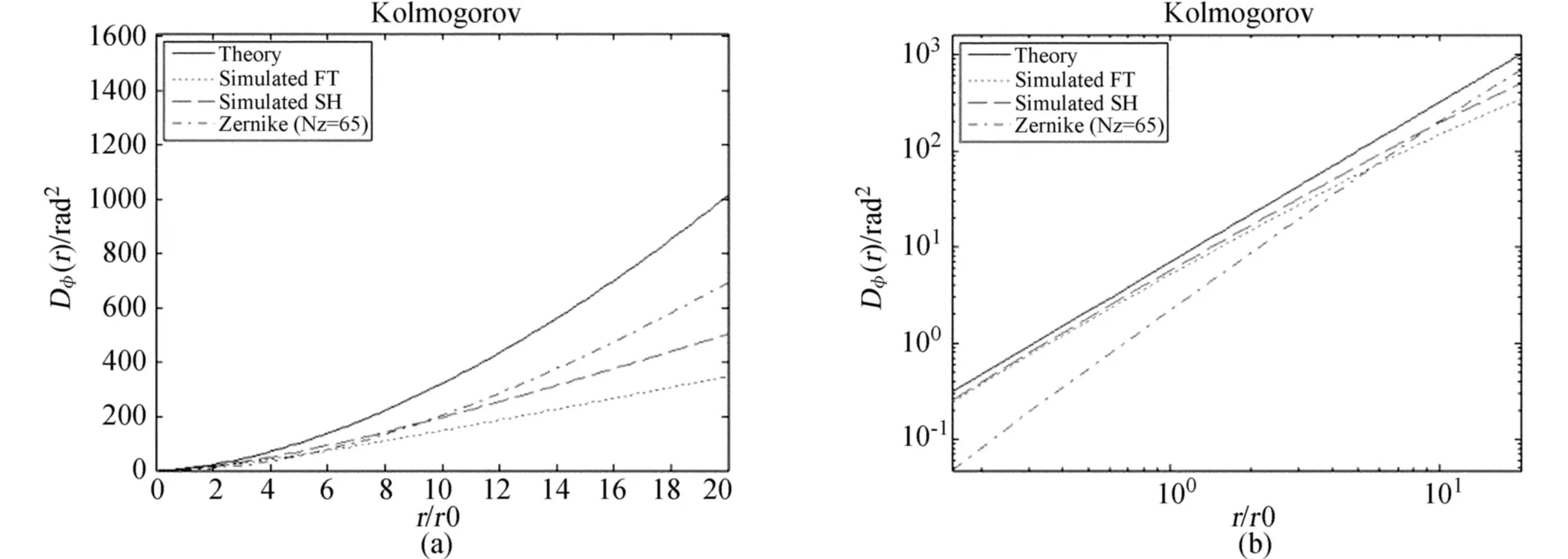
图2 Monte－Carlo相位屏结构函数图中是使用40个独立随机相位屏结构函数系综平均后的对比结果，加入了65阶Zernike多项式模拟结果与次谐低频补偿和直接谱反演结果跟理论值比较，其中(a)和(b)分别为线性视图和对数视图，实线为理论值，长横线、短横线和点横线分别为次谐补偿法、直接谱反演法和Zernike多项式法所得结果Fig.2 Comparison of average structure functions of phase screens generated with different methods.The structure functions are averaged from 40 phase screens generated in the Monte－Carlo simulations with the FFT method，the SH－FFT method，and the Zernike－polynomial method(of the first 65 modes).Theoretical predictions are also shown.The frames(a)and(b)are in the linear and logarithmic scales，respectively.

图3为使用(3)式给出的修正von Kármán相位功率谱模拟得到的相位屏相位结构函数对比。一般来说，湍流内尺度范围基本确定，而外尺度则变化范围很大。因此模拟中给出不同外尺度模拟结果的对比。图3(a)和(b)都设定内尺度为3 mm，其中图3(a)外尺度为100 m，图3(b)外尺度为10 m。对比结果可以发现，使用谱反演一类方法生成的随机相位屏与外尺度有关，尤其在低频部分较为明显。当设定外尺度为10 m时，SH－FFT方法得到结果已经与直接谱反演得到的结果相当。因此，在外尺度小的情况下，使用直接谱反演能获得更高的计算效率。

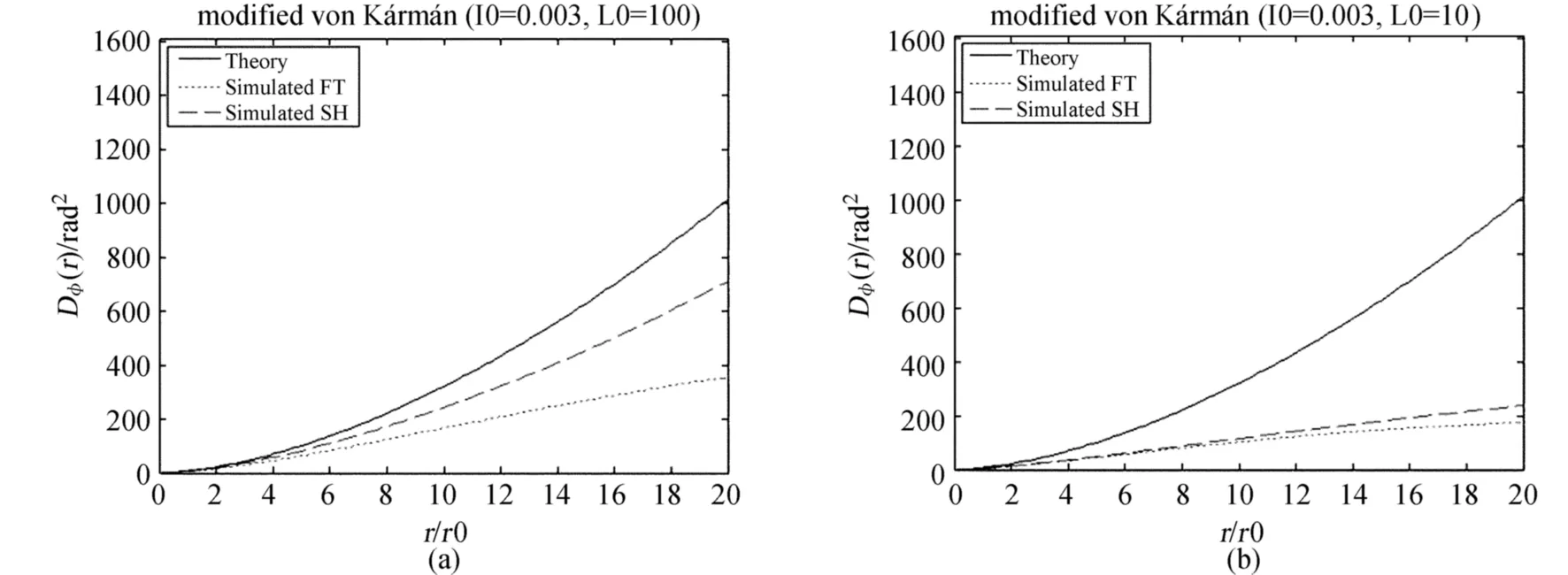
图3 考虑湍流内外尺度的相位屏数值模拟结果分析图中同样是使用40个独立随机相位屏结构函数系综平均后的对比结果。相位屏生成使用修正von Kármán相位PSD。其中，(a)和(b)分别是设定内尺度为3 mm，外尺度分别为10 m和100 m的次谐低频补偿与直接谱反演模拟结果的对比，实线为理论值，长横线、短横线分别为次谐补偿法和直接谱反演法所得结果Fig.3 Comparison of average structure functions of phase screens generated with the SH－FFT and FFT methods under different values of outer scales of turbulence.The structure functions are averaged from 40 phase screens generated in the Moute－Carlo simulations with the FFT and SH－FFT methods.The modified von Kármán phase spectral power density is used for simulations.The frames(a)and(b)are results for outer scales of turbulence equal to 10 m and 100 m，respectively.

通过上述结果对比和分析，可以看出相位屏的数值模拟与使用方法、选用的相位功率谱密度，以及模拟所设定的参数都有很大关系。在使用数值模拟方法时，需要针对具体应用和使用环境，来选择合适的参数得到适合的相位屏模拟结果。本小节给出的结果对比，是考虑天文观测应用，根据云南天文台观测条件设定的相关参数。

2 多相位屏湍流分层模型

为将大气湍流用相位屏的理论表达方式通过多层次模型准确描述，简单将传播经过的第i层大气按照湍流折射率廓线积分，得到厚度为Δzi的湍流层有效的折射率结构常数C2ni。而 C2ni的选择根据具体应用和大气实际情况，以及折射率廓线模型对大气湍流的层次进行划分，以准确描述湍流大气。

例如，M C Roggemann针对成像应用将大气湍流分为4层。每层的高度zi由与之对应的C2n廓线对zi使用矩估计确定。计算方法如下:

式中，0≤m≤7;Δz为整个湍流大气传播路径长度［3］。

本文在建立湍流大气层次模型时，针对天文成像应用，并结合云南天文台的实际观测环境，将湍流大气的层次做重新划分。此处选用HV 10/10折射率结构常数模型［10］。模型描述如下:

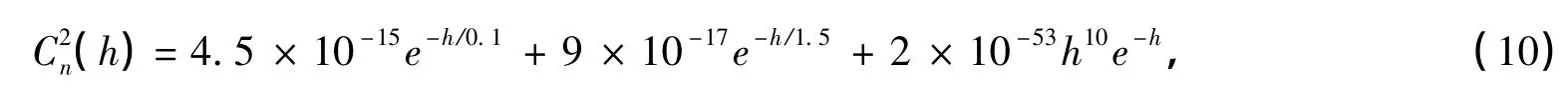
式中，海拔高度单位为km，使用等Rytov指数间隔的方法确定湍流层高度zi和厚度Δzi，并确定相位屏位置。

等Rytov指数间隔，即根据弱起伏湍流性质，设置湍流层间Rytov指数间隔为常数c1，并由此计算得出层间距Δzi，再计算得出相位屏间距［11］。在计算Δzi时，设层间C2ni为常数，且光波为平面波。于是有［2］:

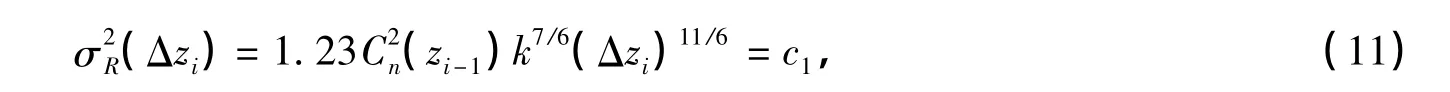
计算得出Δzi，并由zi=zi－1+Δzi/2确定相位屏位置［11］。最终得到描述湍流大气的层次模型。

以云南天文台为例，依据夜间实际观测条件经验值r0=12 cm，并将(10)式给出的HV 10/10模型代入Fried参数定义式计算，设定波长为0.8μm，得到折射率结构常数倍率因子为12。其中r0定义为:

将HV 10/10折射率结构常数模型乘以倍率12，得到近似的折射率结构常数廓线模型。然后使用等Rytov指数间隔方法，设定常数c1=0.07，考虑有效湍流大气为2～20 km，得到4层湍流大气模型。模型及其参数如图4。

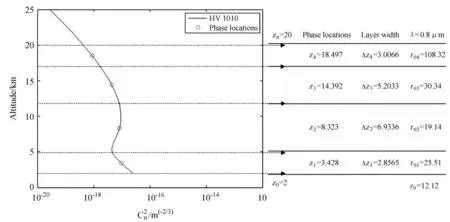
图4 云南天文台湍流层次模型考虑20 km以下湍流影响，基于HV 10/10廓线模型，使用等Rytov指数间隔选取相位屏位置，建立多相位屏层次模型。各层间隔、等效r0和相位屏位置如图右边列表所示。距离单位km，r0单位cmFig.4 A layered model of atmosphere above the Yunnan Observatory.This model only includes effects of turbulences of altitudes under20 km.It is based on the HV 10/10 turbulence model，and using equal Rytov－index intervals to sample heights of phase screens.

3 天文成像的Monte－Carlo模拟

对部分相干光的天文成像过程，可将其近似为信号经过线性系统的过程，该线性系统由光学传递函数(Optical Transfer Function，OTF)表征。这样就将描述互强度传播的Zernike－von Cittert定理简化为关于广义光瞳函数P(r)的卷积成像过程，即Schell定理［1］，并利用傅里叶变换卷积定理有:

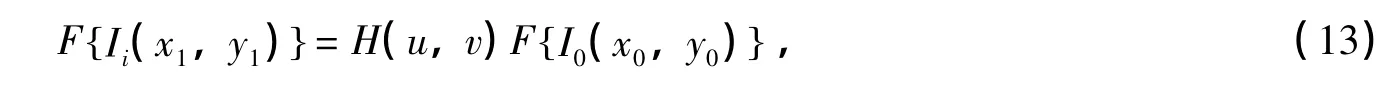
式中，F{}表示傅里叶变换;Ii、I0分别表示经过湍流大气的图像和未经湍流影响的图像;H(u，v)为光学传递函数，定义为［12］:

式中，zf为成像系统的焦距。这样，大气扰动、望远镜衍射以及自适应光学补偿的成像效果都用光学传递函数H(u，v)描述。湍流造成的波前起伏和望远镜本身的像差，以及自适应光学的波前补偿效果都通过P(r)表征。大气湍流造成的波前起伏则由相位屏描述。考虑使用图4中的多相位屏分层模型，最终望远镜光瞳上的相位起伏为沿传播路径相位的线性叠加。忽略望远镜和成像系统固有像差，且在大气相干时间τ0内的光瞳如图5。

通过仿真得到的广义光瞳函数，就可根据(14)式得到大气－望远镜的光学传递函数，并利用(13)式得到短曝光天文图像的数值仿真结果。在此基础上，借助Monte－Carlo方法对多个短曝光仿真结果叠加得到长曝光图像。下面就给出设计的天文成像仿真实验和结果。

本文数值仿真中对点光源目标成像进行模拟，使用超高斯函数描述点光源，有:

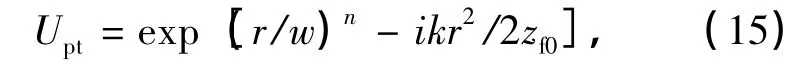
式中，w为成像系统衍射极限宽度，取n=8;当考虑点源光线为来自无穷远处的平面波时，取zf0=0，若考虑为球面波则zf0为传播距离。设成像视场(FOV)为5 arcsec，目标为光线来自无穷远处的平面波点光源。设波长λ=0.55μm，依据云南天文台1.2 m口径望远镜，得到衍射极限为0.13 arcsec。由(15)式，设w=0.13，相位为0，得到的点源目标图像如图6。

在模拟计算中，依据实际系统使成像视场与望远镜实际光瞳对应，视场采样间隔和光瞳采样间隔分别为0.036 arcsec2和5 mm。图6(a)为方便显示，仅截取视场中心0.5 arcsec2范围。

设总r0=12 cm，考虑光沿垂直路径传播成像，利用SH－FFT方法生成随机相位屏并叠加得到如图5的短曝光光瞳函数。由此，根据(14)式计算大气－望远镜系统短曝光传递函数。最后利用图6中的点光源模型，结合(13)式计算得到目标经湍流大气短曝光成像的数值仿真结果，如图7。

图5 大气－望远镜广义光瞳示意图中，望远镜理想光瞳根据云南天文台1.2 m望远镜实际主副镜及副镜支架得到，副镜中心遮拦比为0.17;湍流大气相位屏表示的随机波前起伏单位为弧度 (rad)Fig.5 An example of joint atmosphere－telescope generalized pupil function.The ideal telescope pupil in this example is tailored to the primary/secondary mirrors and mirror scaffolds of the 1.2 m telescope of the Yunnan Observatory.The occlusion ratio of the secondary mirror is0.17.

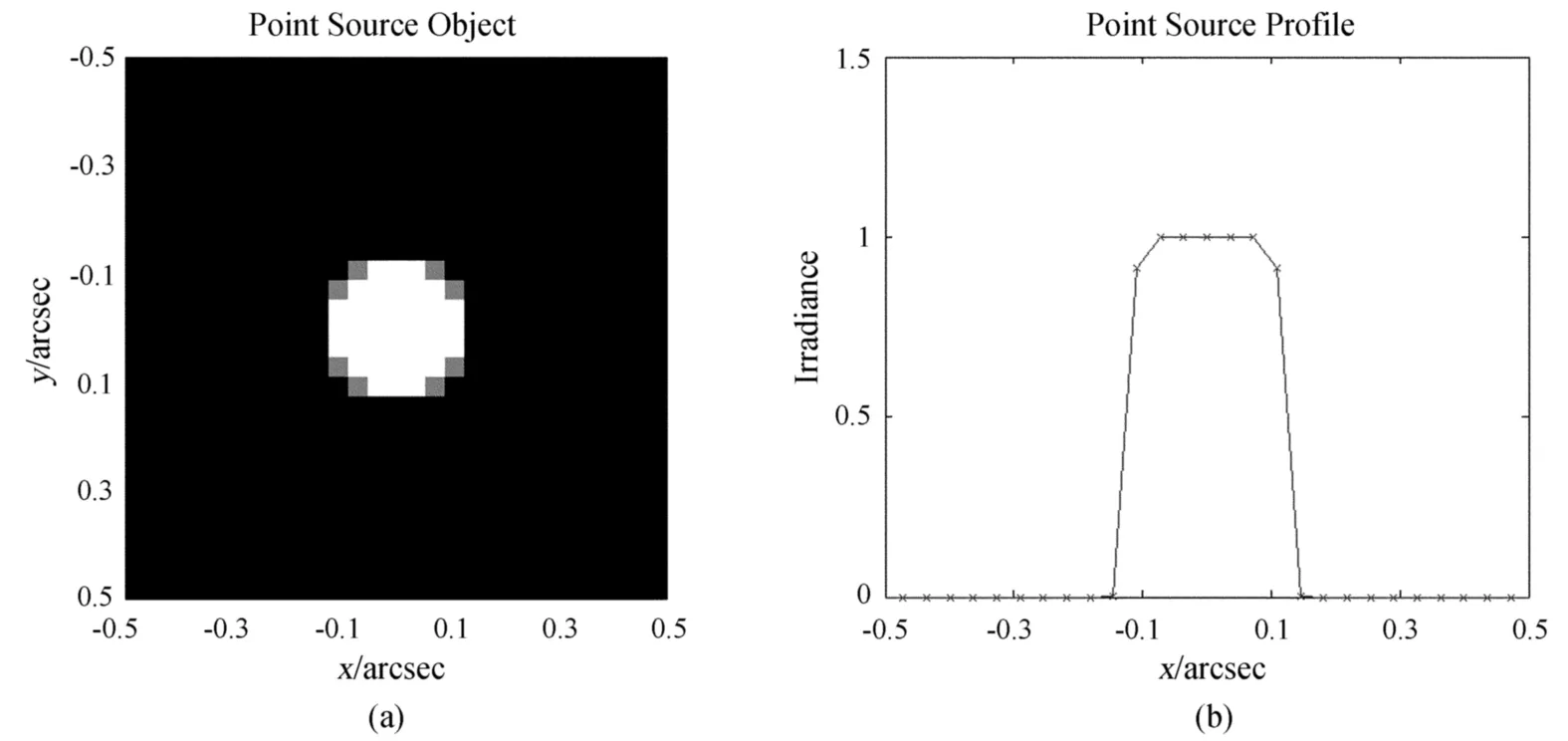
图6 点光源目标模型图中 (a)、(b)分别为点光源目标图像和截面廓线图，图像平面坐标为角秒 (arcsec)Fig.6 Point－Source model.The frames(a)and(b)are the image and profile slice of the point source，respectively.

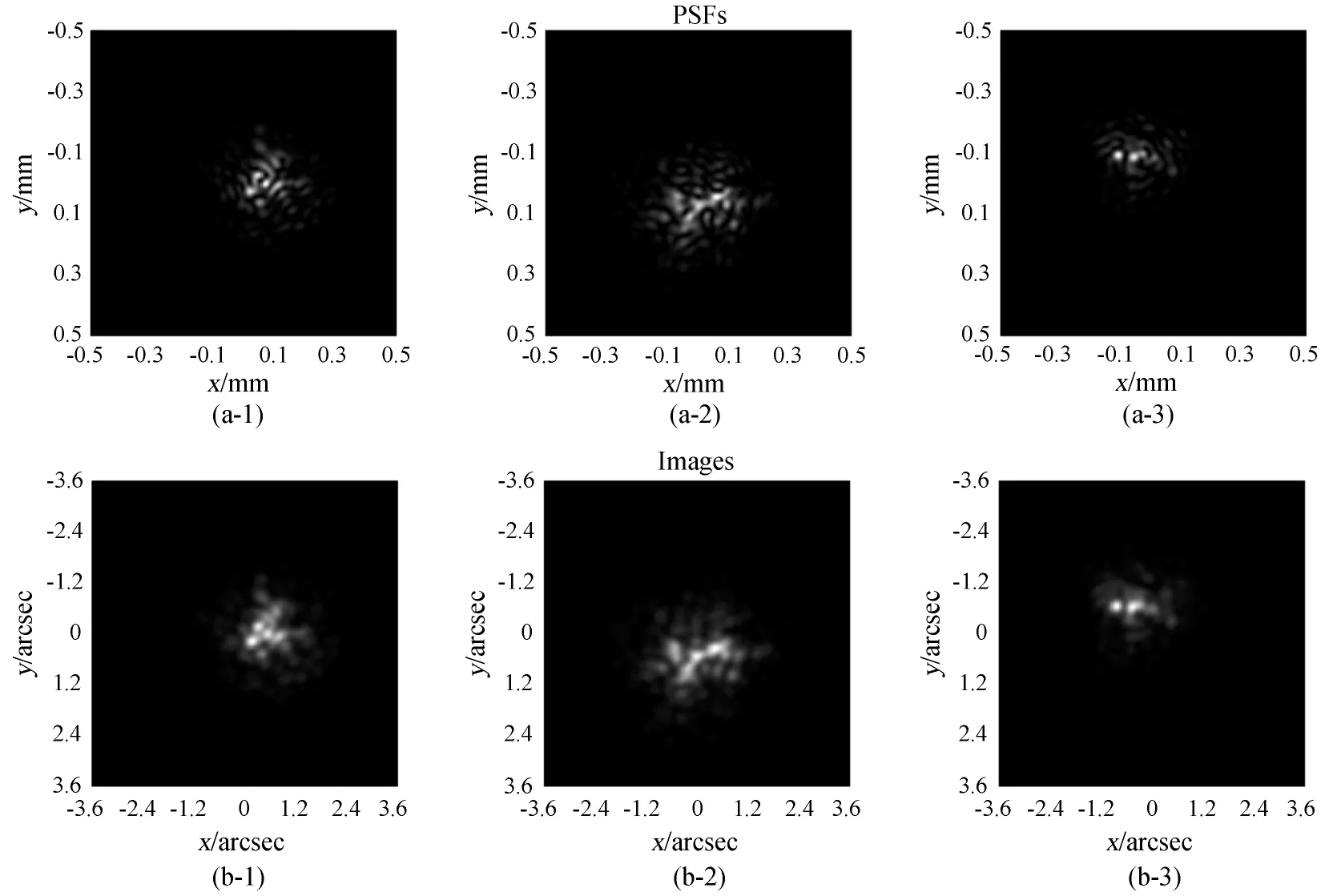
图7 点光源目标短曝光成像仿真结果图(a－1～3)为湍流影响下的大气－望远镜系统短曝光传递函数，图(b－1～3)为分别与之对应的点光源目标图像，图像视场截取7.2 arcsec×7.2 arcsecFig.7 Simulated short－exposure image of a point source.The frames(a－1)to(a－3)are short－exposure PSFs of a joint atmosphere－telescope system.The frames(b－1)to(b－3)are simulated short－exposure images of a point source，in one－to－one correspondence with the PSFs above.The FOV of images is 7.2×7.2 arcsec2.

图7中，第1行3帧图像是利用Monte－Carlo方法得到的3个系统传递函数(Point Spread－Function)随机样本，系统PSF由系统的光学传递函数的傅里叶逆变换取模平方得到:

与图7(a－1～3)PSF分别对应的是其下方点光源短曝光数值仿真图像图7(b－1～3)。从图中不但可以看出湍流随机波前起伏的高阶模式导致的斑纹图样，还可以看出由低阶模式导致的图像抖动和失焦。此外需要注意的是，本文给出的天文成像仿真实验都假设望远镜系统具有理想像质，忽略了成像系统本身的像差影响;同时也忽略了成像系统的探测噪声。

为了对自适应光学(AO)成像系统的图像补偿效果进行数值仿真，可以通过假设自适应光学系统能够实现对波前模式的理想改正，且忽略波前探测误差和模式混淆误差。可将随机生成的湍流扰动波前展开为Zernike波前模式。在此基础上，除去自适应光学系统改正的波前模式便可得到自适应光学理想补偿之后的残余波前。利用残余的随机波前对目标成像，就得到了自适应光学部分补偿之后的成像仿真结果。

同样使用上述数值仿真实验参数，如图8，为自适应光学理想情况下的部分补偿成像过程示意。设定自适应光学补偿系统的理想Zernike模式补偿阶数为35阶。图8(a)为据此展开得到的前35阶波前模式，图8(b)为湍流扰动波前，假设理想补偿之后得到图8(c)残余波前，由此得到图8(f)部分补偿图像。图8(e)是由湍流波前得到的未补偿图像。

对于湍流大气空域统计特性的分析，是通过泰勒近似，将时域统计特性与空域统计特性相关联。在广义平稳条件下，将折射率起伏的系综平均等效为时间平均进行分析。这样，利用Monte－Carlo方法，通过随机相位屏多个统计样本的生成并叠加就可得到长曝光天文图像。实验条件与先前相同，对点源目标的长曝光仿真结果如图9。

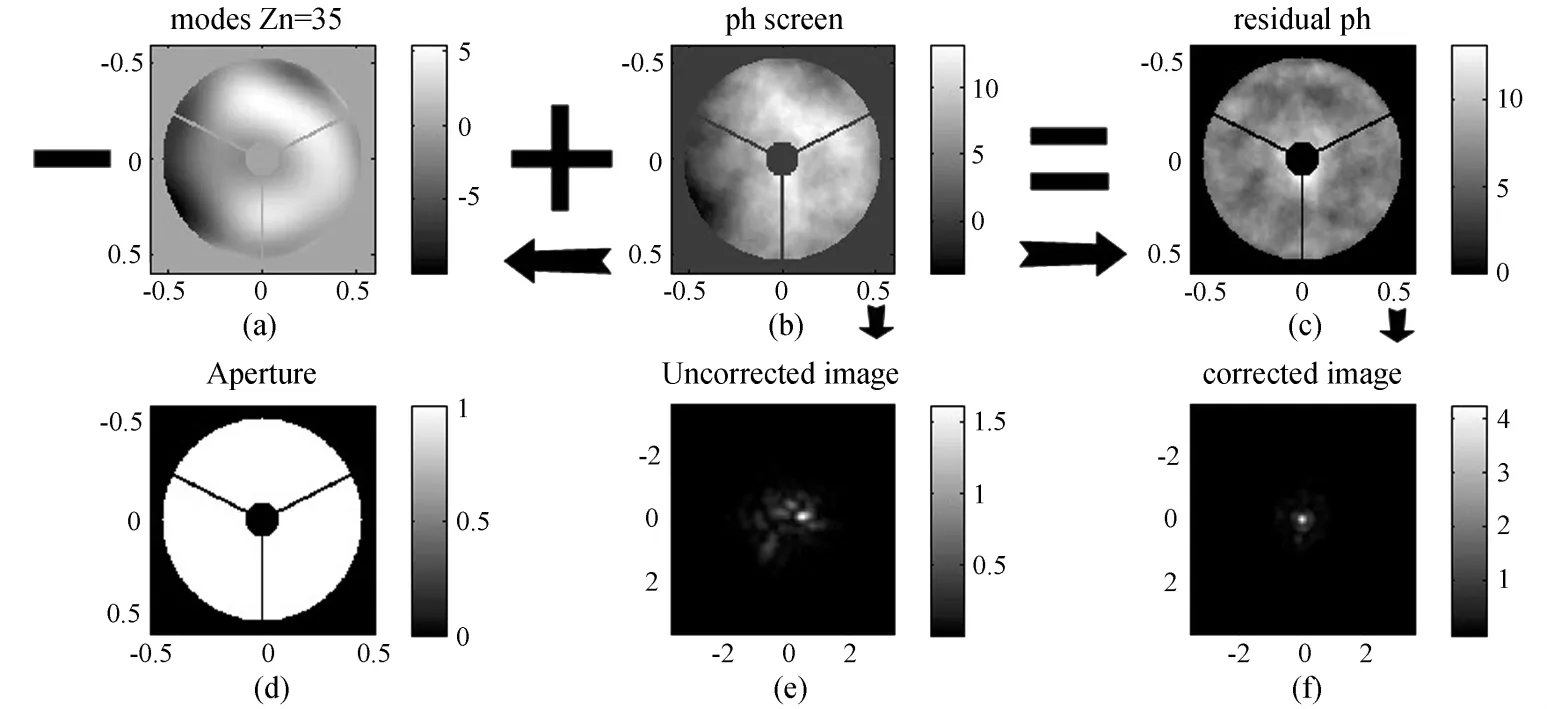
图8 自适应光学成像系统理想改正的部分补偿成像过程数值仿真图(a)是由湍流随机波前展开得到的前35阶Zernike模式，假设为自适应光学系统补偿等效的理想模式改正阶数。图(c)为残余波前;图(e)、(f)分别为未补偿和补偿后的仿真结果Fig.8 Illustration of simulation of partial compensation of image by an AO system.The frame(a)is the wavefront aberration of the phase screen of the first 35 Zernike modes generated with the Monte Carlo Method taken to be the ideal compensation of the AO system.The frame(c)shows the residual aberration after the compensation.The frames(e)and(f)are simulated short－exposure point－source images before and after compensation，respectively.

图9 点光源目标成像的Monte－Carlo模拟图(a)为200帧湍流点源图像叠加结果，等效于未经自适应光学补偿的长曝光点源像;图(b)为单帧自适应光学补偿成像仿真结果;图(c)为200帧自适应光学补偿点源图像叠加结果，等效于自适应光学补偿后的长曝光点源像Fig.9 Results of point－source images in our Monte－Carlo simulation.The frame(a)shows the image of a point source of200 frames influenced by turbulences(i.e.long－exposure image without any compensation of the AO system.The frame(b)is a single－frame image after the compensation.The frame(c)is an average of200 frames after the compensation，which shows the corrected point spread function.

图9中，图(a)为点源目标的长曝光仿真成像结果，使用200帧短曝光仿真图像叠加获得。若设大气相干时间τ0≈10 ms，则相当于曝光时间为2 s的成像结果。图(b)和(c)分别为单帧和200帧叠加的自适应光学理想补偿成像结果，设自适应光学成像补偿的理想模式补偿阶数为35阶。这一设定是依据云南天文台1.2 m望远镜61单元自适应光学成像系统以及相关分析得出的估计值［13－15］。所得结果中，长曝光点源图像SR值为0.014。自适应光学补偿后的长曝光结果SR值为0.37。仿真结果与实际系统经验值基本吻合［15］。

图10为配备61单元自适应光学成像补偿系统的云南天文台1.2 m望远镜对双星Castor的观测结果。图7(b－1～3)可与实测得到的图10(a－1～3)比较，需要注意区别的是，在图10(a－1～3)的实测结果中忽略了Piston模式项，且改正了图像抖动。图9(a～c)中仿真成像结果可与图10(b～d)的实测结果分别对应比较，比较时要注意视场大小的区别。

图10 CASTOR(α Gem)观测图像其中(a－1～3)为连续3帧短曝光散斑图，正好体现出湍流引起的折射率随机起伏由强至弱的一个时域变化过程;(b)为长曝光图像，(c)为自适应光学补偿后的短曝光图像，(d)为自适应光学补偿后的长曝光图像。云南天文台1.2 m望远镜观测于2008年Fig.10 Observational results for the CASTOR(α Gem).The frames(a－1)to(a－3)are 3 frames of short－exposure speckle images.The frame(b)is the uncompensated long－exposure image.The frame(c)is a short－exposure image after the compensation with AO.The frame(d)is the long－exposure image after the compensation.(The observation was carried out with the 1.2 m telescope of the Yunnan Observatory and the attached 61－element AO system in2008).

4 总结与展望

根据大气湍流统计性质，在对相位屏生成方法的分析和优化基础上，本文给出了天文成像数值仿真的一套完整方法，并结合云南天文台观测条件设计了数值仿真实验，给出了结果。本文所提出的数值仿真方法，可应用于克服湍流大气影响的地基高分辨天文成像技术研究。借助Monte－Carlo方法，通过随机相位屏多个统计样本的生成，对湍流大气的空域统计特性进行分析和研究。对天文图像重建技术和用于天文观测的自适应光学技术研究有重要意义。

［1］顾德门.统计光学 ［M］.秦克诚，译.北京:科学出版社，1992.

［2］Larry C Andrews，Ronald L Phillips.Laser Beam Propagation through Random Media ［M］.Bellingham:SPIE Press，2005.

［3］Michael C Roggemann，Byron Welsh.Imaging through Turbulence ［M］.Boca Raton:CRC Press，1996.

［4］Benjamin L Mcglamery.Restoration of Turbulence－Degraded Images ［J］.Journal of the Optical Society of America，1967，57(3):293－296.

［5］Lane R，Glindemann A，Dainty J.Simulation of a Kolmogorov Phase Screen ［J］.Waves in Random Media，1992，2(3):209－224.

［6］Welsh B M，C Dainty.Fourier－Series－Based Atmospheric Phase Screen Generator for Simulating Anisoplanatic Geometries and Temporal Evolution ［3125－37］［C］//Luc R Bossonnette，Christopher Dainty.Progagation and Imaging through the Atmosphere.Proceedings of SPIE，1997，3125:327.

［7］Rebecca J Eckert，Matthew E Goda.Polar Phase Screens:a Comparative Analysis with Other Methods of Random Phase Screen Generation ［C］//Atmospheric Optical Modeling，Measurement，and Simulation II.Proceeding of SPIE，2006，6303:1.

［8］Nicolas A Roddier.Atmospheric Wavefront Simulation Using Zernike Polynomials ［J］.Optical Engineering，1990，29:1174－1180.

［9］Hans Jakobsson.Simulations of Time Series of Atmospherically Distorted Wave Fronts ［J］.Applied Optics，1996，35(9):1561－1565.

［10］John W Hardy.Adaptive Optics for Astronomical Telescopes［M］.Oxford:Oxford University Press，1998.

［11］钱仙妹，朱文越，饶瑞中.非均匀湍流路径上光传播数值模拟的相位屏分布 ［J］.物理学报，2009，58(9):6633－6639.Qian Xianmei，Zhu Wenyue，Rao Ruizhong.Phase Screen Distribution for Simulating Laser Propagation Along an Inhomogeneous Atmospheric Path ［J］.Acta Physica Sinica，2009，58(9):6633－6639.

［12］古德曼.傅里叶光学导论 ［M］.秦克诚，译.北京:电子工业出版社，2006.

［13］李新阳，姜文汉，王春红，等.湍流大气中哈特曼传感器的模式波前复原误差 ［J］.强激光与粒子束，2000，12(3):149－154.Li Xinyang，Jiang Wenhan，Wang Chunhong，et al.Modal Reconstruction Error of the Hartmann Sensor on Measuring the Atmosphere Disturbed Wavefront［J］.High Power Laser and Particle Beams，2000，12(3):149－154.

［14］Tang Guomao，Rao Changhui，Shen Feng，et al.Performance and Test Results of a 61－element Adaptive Optics System on the 1.2m Telescope of Yunnan Observatory ［C］//Jiang Wenhan，Robert K Tyson.Adaptive Optics and Applications II.Proceedings of SPIE，2002，4926:13－19.

［15］Rao Changhui，Jiang Wenhan，Zhang Yudong，et al.Performance on the 61－element Upgraded Adaptive Optical System for 1.2m Telescope of the Yunnan Observatory［C］//Jiang Wenhan，Suzuki，Yoshiji.Adaptive Optics and Applications III.Proceedings of SPIE，2004，5639:11－20.