基于连续小波系数非线性流形学习的冲击特征提取方法
栗茂林,梁 霖,王孙安,庄 健
(西安交通大学 机械工程学院,西安 710049)
基于连续小波系数非线性流形学习的冲击特征提取方法
栗茂林,梁 霖,王孙安,庄 健
(西安交通大学 机械工程学院,西安 710049)
为了提取机械设备故障引发的冲击成分,提出了一种基于连续小波系数非线性流形学习的冲击故障特征提取方法。首先,基于小波熵方法优化出最优的Morlet小波波形参数,实现与冲击特征成分的最佳匹配,获取包含冲击特征信息的最优小波系数矩阵。其次,采用局部切空间排列算法对最优小波系数矩阵进行非线性约简,并基于峭度指标最大化原则,确定出特征空间中的有效低维嵌入,从而提取出最优的冲击故障特征。最后,通过仿真数据和工程实际的应用对比分析,表明该方法采用了局部线性化和全局排列的思想,与线性奇异值分解方法相比,不仅在时域上提取出峭度更大的微弱冲击特征成分,而且在频谱中还提取出了相应的低频故障特征。
特征提取;连续小波变换;非线性流形学习;冲击故障
在机械设备的故障中,冲击类故障占有较高的比例,如动静件间的周期性碰撞、缺陷轴承或齿轮运行时的瞬时冲击等。冲击响应中包含了周期性的反映固有频率的有阻尼简谐振动,其中,冲击力大小、固有特征及冲击重复周期等都是诊断的重要信息。然而由于设备的早期故障,往往使得这些周期冲击简谐振动特征被噪声淹没而不易识别。小波变换作为一种时频分析方法是研究非平稳冲击故障特征的热门工具。
在小波变换中,连续小波变换的尺度连续变化可以充分细致地刻划信号的局部形态。采用与冲击特征波形近似的基小波进行连续小波变换时,冲击特征分量的变换系数与噪声等其他分量不同,因此通过时频分布图可以观察到变换系数的周期性变化情况,如文献[1]通过最优Morlet小波变换在时间-尺度分布中反映出轴承和齿轮振动信号中的周期分量;文献[2]通过Haar小波变换的灰度图检测出变速箱周期性的冲击特征。但另一方面,时频分布图虽然可以直观形象地反映出各尺度下的小波系数变化情况,但这种表示方法不利于后续的诊断识别处理。因此,文献[3]对变换系数进行处理,通过统计尺度-小波能量谱的分布特性曲线提取出更好的信号特征;文献[4]认为瞬态成分和噪声的小波变换系数具有不同的统计分布特征,因此通过统计检验方法提取出小波系数中的瞬态成分。这些研究成果直接对部分尺度的小波系数分析处理,对人员依赖性强,需要先验知识,容易导致诊断信息的丢失。
研究表明,冲击特征信息主要被分解在小波变换系数的部分尺度中,使小波变换系数矩阵具有一定的稀疏性。因此,对矩阵进行稀疏性分解的奇异值分解(singular value decomposition,SVD)方法被应用于连续小波系数的特征提取中[5-6],其思路是对小波系数矩阵用线性方法来逼近系统的空间流形,通过分解的主要特征向量得到系数矩阵中的固有成分,即冲击特征。这样既体现了连续小波变换的高分辨率分析的优点,又克服了连续小波变换各尺度系数间的冗余性。但是,研究表明奇异值分解本身属于线性学习方法,忽略了系数矩阵数据集存在的凸凹性,仅能提取出其中的线性特征,不能找到真正的数据分布结构。
而非线性流形学习方法为基于数据分布的内在结构分析提供了一种新的研究途径,其基本思想是:高维观测空间中的点由少数独立变量的共同作用在观测空间张成一个流形,在尽可能地保证数据间的几何关系和距离测度不变的前提下,有效地展开观测空间卷曲的流形来发现内在的主要变量,实现对数据集的约简。这就意味着流形学习比传统线性约简方法更能体现事物的本质,更有利于对数据的理解和进一步处理。如黎敏等人对高维相空间中重构的流形拓扑结构进行综合信息提取[7];蒋全胜等人运用拉普拉斯特征映射的非线性降维方法保留了振动信号中内含的整体几何结构信息[8],这些研究为非线性流形学习在故障诊断中的应用开辟了思路。
本文针对早期故障诊断中微弱冲击特征提取的问题,将适用于故障特征流形空间的局部切空间排列算法(local tangent space alignment,LTSA)应用于连续小波变换(continuous wavelet transform,CWT)最优系数矩阵的稀疏性分析中,提出基于连续小波系数非线性流形学习的冲击特征提取方法CWT-LTSA。其中,基于峭度指标最大化原则确定有效的低维嵌入向量,提取最优的冲击故障特征。通过仿真数据和实际案例的应用对比分析,表明方法的有效性。
1 连续小波变换CWT
对于能量有限的信号x(t),其连续小波变换可以表示为与小波函数的内积[9],即:
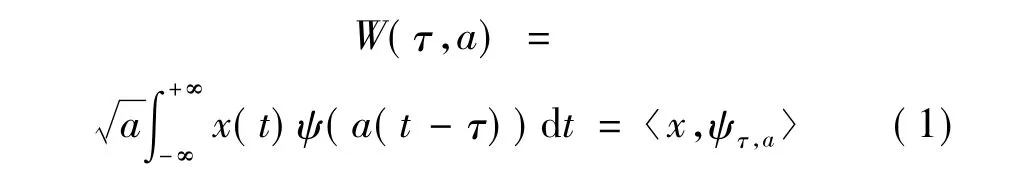
式中:τ、a∈L2;τ为时间位置参数;a为尺度参数;ψ(t)为小波函数;ψτ,a(t)为基小波函数。
对于存在傅里叶变换对的基小波函数,由傅里叶变换的卷积性质,式(1)又可表示为:

式中:F-1表示傅里叶逆变换,X(f)和ψ*(f)是x(t)和ψ(t)的傅里叶变换。
式(2)变换后的小波系数矩阵W(τ,a)通过时间和尺度的变化度量了信号x(t)与小波ψ(t)之间的相似程度。信号中的特征信息(如频率和周期重复性)反映在系数矩阵的变化中。
2 局部切空间排列算法LTSA
局部切空间排列算法LTSA通过逼近每个样本的切空间来构建低维流形的局部几何,并利用局部切空间排列求出整体低维嵌入坐标,恢复出流形等距的低维空间子集[10]。算法包括了两个过程。
2.1 局部线性拟合

2.2 局部坐标全局排列


为了唯一地确定T,引入约束TTT=Id。
由于全1向量e是矩阵B的零特征值对应的特征向量,所以取矩阵B的第2到第(d+1)个最小的特征值对应的特征向量所组成的矩阵就是所求的T,即为描述了样本空间矩阵X中非线性主流形的正交低维全局坐标映射矩阵。
3 基于流形的最优小波系数特征提取
基于全局思想的流形学习方法,如ISOMAP,要求流形所对应低维空间的子集是凸的,才能保证构造的流形上距离远的点之间的联系是准确的。然而,基于局部思想的LTSA方法只考虑流形邻近点之间的关系,不要求流形所对应低维空间的子集是凸的,有着更广泛的适用对象。因此,本文结合冲击特征的特点,提出了一种连续小波系数局部切空间流形学习的冲击特征提取方法CWT-LTSA。通过对最优连续小波系数矩阵流形的学习,结合峭度指标最大化原则,提取出时频分布中的低维嵌入,实现冲击特征的提取。具体的步骤如下:
步骤1基于Morlet小波的样本空间获取
由于Morlet小波与机械振动中的瞬态冲击特征比较近似,可以保证与信号较好的匹配性,因此是提取冲击特征的有效小波函数,其数学表达如下:
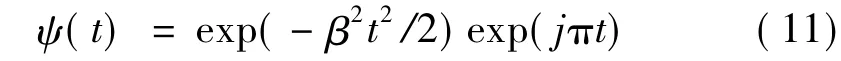
对于机械振动信号来说,通常采用其实部作为基小波,即:

式中:β为波形参数,控制着小波波形的衰减率。为了与冲击信号取得最优匹配,采用小波熵[1]确定最优波形参数 βop,获取最优系数矩阵 Wβop(τ,a)。

式中:j为波形参数β的变化,通常在[0.1,2]范围内取值,S(Wj)为小波系数矩阵的信息熵。
步骤2样本空间的局部邻域选取

研究表明,不同的邻域点k将获得不同的嵌入效果:邻域太小使得切空间易非满秩,而过大又容易损失局部几何信息[10],本文依据经验取值。
步骤3局部线性投影
对每个样本向量点的邻域,计算中心化矩阵XixieT的d个最大奇异值对应的左奇异向量,并将这d个左奇异向量组成矩阵Qi。
步骤4低维特征的提取
为了提取最优的冲击特征,以反映冲击特征较好的峭度指标作为衡量指标,即最优的低维嵌入波形uop将具有最大的峭度值。

式中:Kurtosis为峭度指标。
在这里,需要指出的是,由于尺度的连续变化,冲击特征分量的小波变换系数在尺度范围内将具有一定的相似性,因此,提取的低维全局坐标矩阵T=[u2,u3,…,ud+1]T中的某些维度上会出现类似文献[11]中提到的坍塌现象,即由于相似度较高,数据在约简后的特征空间中表现为前几维的坐标值具有近似性,但由于冲击分量幅值、初相有差异,并不影响其正交性。另外,由式(10)引入的约束TTT=Id可知,低维全局坐标矩阵T是归一化的特征向量,提取的波形显示归一化幅值,采用与幅值大小无关的峭度指标有效地反映归一化波形的冲击衰减程度。
4 仿真试验与工程应用分析
4.1 仿真试验分析
为验证方法的有效性,模拟一周期的冲击衰减信号,并包含一定的噪声成分,其波形如图1所示。对模拟数据采用CWT-LTSA方法进行计算,其中最优波形参数 βop为0.3,尺度参数 a∈[1,20],步长为0.1,邻域点k依经验取为10,嵌入维数d取为5。
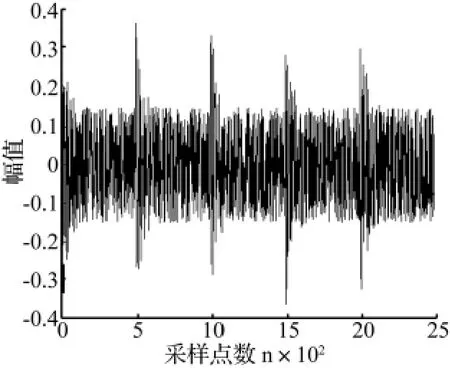
图1 加噪的冲击模拟信号波形Fig.1 The impact noise simulation signal waveform
经计算,提取低维全局坐标下的波形峭度变化情况如图2所示,最大的峭度值为15.92,对应最优嵌入维数dop=1,提取的波形如图3所示。为了对比学习效果,采用CWT-SVD方法提取的冲击信号波形如图4所示,波形的峭度指标值仅为7.56。对比可知,在时域波形中,CWT-SVD方法也提取出了信号的冲击成分,但CWT-LTSA的效果更好,具有更小的噪声干扰,且冲击特征的周期性更好。
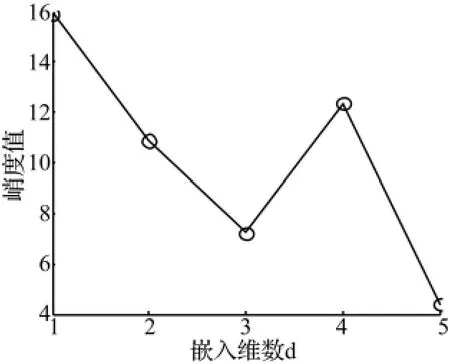
图2 低维嵌入空间下的峭度值Fig.2 The kurtosis index in low-dimensional embedding space

图3 CWT-LTSA提取的冲击信号波形Fig.3 The impact signal waveform extracted by CWT-LTSA
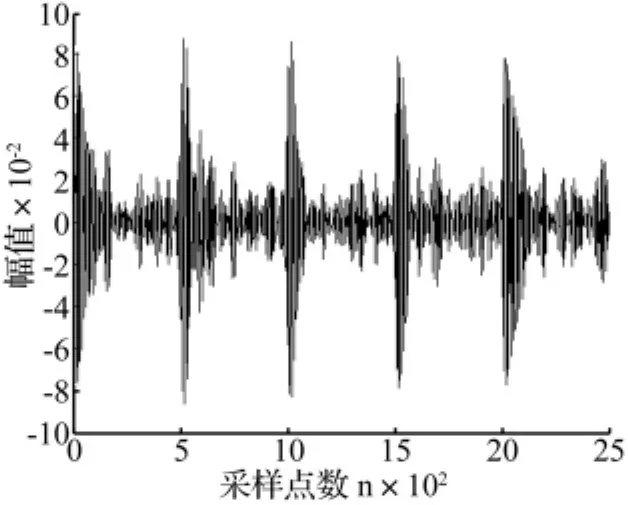
图4 CWT-SVD提取的冲击信号波形Fig.4 The impact signal waveform extracted by CWT-SVD
分析可知,SVD分解的是两两正交的线性子空间,而LTSA提取的全局坐标是非线性子空间。由于SVD将小波系数矩阵作为整体线性化考虑,使得噪声信息在各个子空间中均有一定的投影,冲击分量的投影也因丢掉一些细节信息受到一定程度的影响。相比而言,LTSA算法通过局部邻域的线性化处理以及全局排列的策略获取非线性子空间,非线性坐标更加符合由冲击分量形成的连续变化的局部几何结构,而噪声分量由于随机波动形成变化不连续的局部结构,通过局部线性化处理平滑掉大部分噪声分量。因此,冲击分量在非线性子空间中的投影幅值大于线性子空间的幅值,且相当一部分的噪声信息被分解在其他子空间中,从而使得冲击分量所在的子空间中具有较小的噪声干扰。
4.2 滚动轴承故障特征的提取分析
现选取信噪比较低的轴承故障测试信号进行应用分析。由加速度传感器在轴承座上拾取308轴承的轻微外环故障得到的信号如图5所示,轴承转速为1 600 r/min,采样频率为 40 k,故障特征频率为 82.05 Hz。波形中由故障引起的周期冲击衰减成分受到较大的噪声干扰而被淹没,无法观察到周期分量。图6所示的对应频谱中也无法体现故障特征频率。
首先,基于Morlet小波变换对轴承故障振动信号进行分析处理,尺度参数 a∈[1,20],步长为 0.1,最优波形参数βop为0.2。在最优包络的小波变化系数中,根据系数能量最大的尺度5.5对小波系数矩阵进行切片提取的波形如图7所示。从图中可以看出,小波系数中包含的特征成分及周期性变化不明显,需要进一步的分析处理。
其次,采取CWT-LTSA来提取小波系数矩阵中的冲击特征,获取的低维全局坐标下的波形峭度变化情况如图8所示,选取峭度指标值19.11对应的最优低维嵌入dop=3作为提取的波形,如图9所示。图10所示为其他3个低维嵌入(d=1,d=2和d=4)的波形。与图9所示的最优波形具有一定的相似性,即提取出一系列的冲击衰减分量,但提取质量较差。另外,采用CWT-SVD方法进行对比分析,其提取的冲击波形如图11所示,峭度指标值为12.20。由此可见,仅从提取波形的冲击成分来看,显然非线性流形学习的特征提取能力更强,提取的冲击成分更明显,噪声干扰更小。

图5 轴承外环故障波形Fig.5 The bearing outer ring fault signal waveform

图6 轴承外环故障波形频谱的低频区Fig.6 The low-frequency region of the bearing outer ring fault signal frequency spectrum
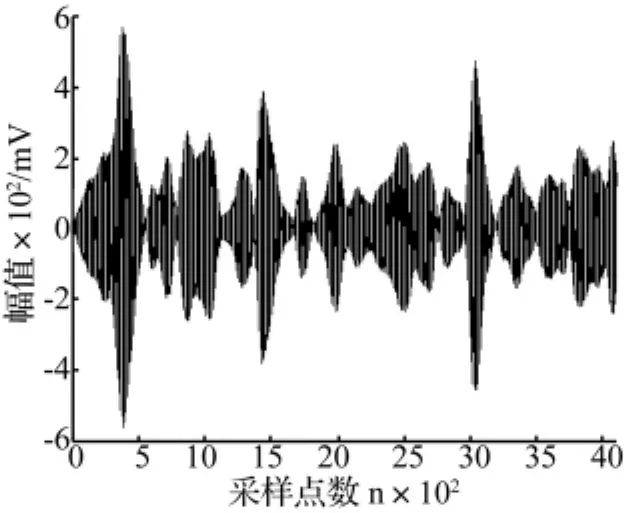
图7 CWT系数的切片波形Fig.7 The slice waveform of CWT coefficients

图8 不同嵌入维数下的峭度值Fig.8 The kurtosis index in embedding space

图9 CWT-LTSA提取的外环故障冲击波形Fig.9 The outer ring fault impact waveform extracted by CWT-LTSA

图10 其他嵌入维数中的外环故障冲击波形Fig.10 The outer ring fault impact waveform in the other embedding space
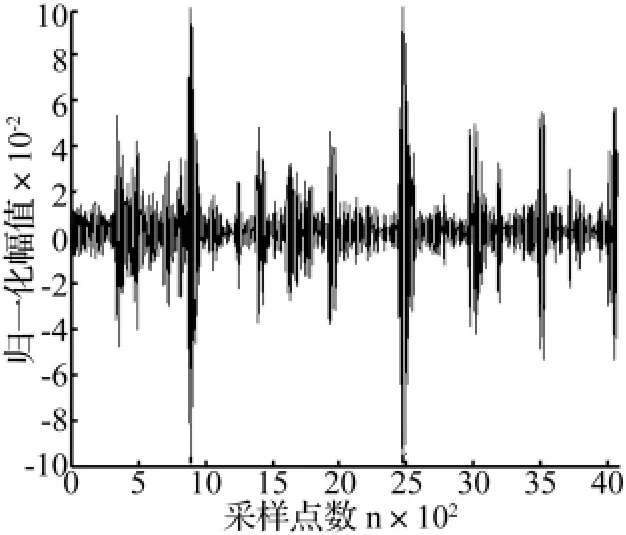
图11 CWT-SVD提取的外环故障冲击波形Fig.11 The outer ring fault impact waveform extracted by CWT-SVD
另外,从频域角度来看,图12所示为非线性流形学习和奇异值分解提取波形的频谱同原始波形频谱的对比图。由频率组成可见,将小波系数矩阵作为整体线性化考虑的CWT-SVD方法,将信息分解至不同的子空间中。由于各子空间包含的信息成分不同,重构提取过程相当于带通滤波,频率成分集中在2 kHz-5 kHz范围,没有提取出82.05 Hz低频故障特征频率。而CWT-LTSA方法通过局部邻域的线性化处理以及全局排列后的特征提取策略,提取的低维嵌入波形的频谱中不仅包含冲击特征对应的主要频带,还提取出系数矩阵中局部邻域间的变化信息,即小波系数值的周期性波动,使得如图13所示的频谱低频区存在82.05 Hz的外环故障特征频率,更好地满足特征提取的需要。
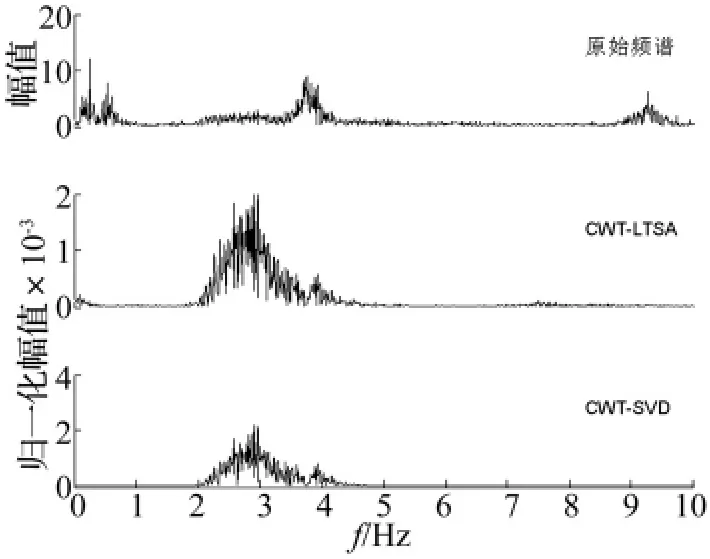
图12 两种方法提取波形的频谱与原始波形频谱的对比Fig.12 The frequency spectrum comparison with the extracted signals by two methods and the original waveform

图13 CWT-LTSA提取外环故障波形频谱的低频区Fig.13 The low-frequency region of the bearing outer ring fault signal frequency spectrum extracted by CWT-LTSA
为了进一步验证非线性流形学习提取冲击特征的能力,选择308轴承的内环故障数据进行分析。转速为1 600 r/min,采样频率为40 k,原始波形和频谱分别如图14和15所示,其中,原始波形的峭度值为9.38,故障的特征频率为131.3 Hz。在原始波形的频谱中,故障特征成分被107.4 Hz和156.2 Hz的两个分量干扰无法识别。

图14 内环故障原始波形Fig.14 The bearing inner ring fault signal waveform

图15 内环故障原始波形频谱的低频区Fig.15 The low-frequency region of the bearing inner ring fault signal frequency spectrum
采用CWT-LTSA方法提取的冲击波形如图16所示,峭度值为14.58(对应第2维低维嵌入),噪声成分明显减少,频谱如图17所示,131.3 Hz的故障特征频率被有效地提取出来。CWT-SVD提取的效果如图18所示,故障特征频率没有被有效分离出来,由此可见本文所提方法的有效性。

图16 CWT-LTSA提取的内环故障冲击波形Fig.16 The inner ring fault impact waveform extracted by CWT-LTSA

图17 CWT-LTSA提取内环故障波形频谱的低频区Fig.17 The low-frequency region of the bearing inner ring fault signal frequency spectrum extracted by CWT-LTSA

图18 CWT-SVD提取的内环故障波形频谱的低频区Fig.18 The low-frequency region of the bearing inner ring fault signal frequency spectrum extracted by CWT-SVD
5 结论
本文针对连续小波变换在冲击特征提取应用中存在的不足,采样局部切空间排列算法,提出了一种基于连续小波系数非线性流形学习的冲击故障特征提取方法。该方法利用局部切空间排列算法,对连续小波变换的最优高维系数矩阵进行非线性变换,基于峭度指标最大化原则,在特征空间中提取出反映冲击故障的低维嵌入。仿真数据和滚动轴承内外环故障样本的应用表明,与线性奇异值分解方法相比,由于非线性切空间排列流形学习方法考虑了样本空间中数据集的局部变化信息,因此,不仅在时域上提取出更完整的微弱冲击特征成分,而且在频谱中提取出了低频故障特征分量,更好地满足了诊断特征的提取需求。
另外,局部切空间排列算法的提取效果较奇异值分解算法好,但在一定程度上受到邻域点等参数选取和样本均匀性的影响,因此,后续将重点研究邻域点的自适应选取及样本对嵌入结果的影响。
[1]林 京,屈梁生.基于连续小波变换的信号检测技术与故障诊断[J].机械工程学报,2000,36(2):95-100.
[2]张梅军,唐 建,陈江海.基于连续小波灰度图的变速箱故障诊断[J].振动、测试与诊断,2007,27(1):65-66.
[3]刘 刚,屈梁生.应用连续小波变换提取机械故障的特征[J].西安交通大学学报,2000,34(11):74-79.
[4]朱忠奎,顾 军,芮延年,等.基于连续小波和统计检验的瞬态成分检测与应用[J].振动工程学报,2006,19(4):559-565.
[5]梁 霖,徐光华,侯成刚.基于奇异值分解的连续小波消噪方法[J].西安交通大学学报,2004,38(9):904-908.
[6]Brenner M J.Nonstationary dynamics data analysis with wavelet-SVD filtering[J].Mechanical systems and signal processing,2003,17(4):765-786.
[7]黎 敏,徐金梧,阳建宏,等.一种基于流形拓扑结构的轴承故障分类方法[J].控制工程,2009,16(3):358-362.
[8]蒋全胜,贾民平,胡建中,等.基于拉普拉斯特征映射的故障模式识别方法[J].系统仿真学报,2008,20(20):5710-5713.
[9] Mallat S.A theory for multiresolution signal decomposition:the wavelet representation[J].IEEE Trans Pattern Analysis and Machine Intelligence,1989,11(7):674-693.
[10] Zhang Z Y,Zha H Y.Principal manifolds and nonlinear dimensionality reduction via tangent space alignment[J].SIAM JournalofScientific Computing,2004,26(1):313-338.
[11]詹德川,周志华.基于流形学习的多示例回归算法[J].计算机学报,2006,29(11):1948-1955.
Mechanical impact feature extraction method based on nonlinear manifold learning of continuous wavelet coefficients
LI Mao-lin,LIANG Lin,WANG Sun-an,ZHUANG Jian
(School of Mechanical Engineering,Xi'an Jiaotong University,Xi'an 710049,China)
To acquire an impact component aroused by mechanical fault,a novel feature extraction method based on nonlinear manifold learning of continuous wavelet coefficients was put forward.Firstly,the wavelet entropy method was adopted to optimize the Morlet wavelet shape factor in order to match with the impact components to obtain the optimal continuous wavelet coefficients.Secondly,the nonlinear manifold learning algorithm named local tangent space alignment was used to reduce the optimal wavelet coefficients matrix,and according to the principle of the maximum kurtosis index,the low-dimensional embedded vectors introduced to reflect impact failures were extracted from the global coordinate feature matrix. Finally, simulations and industrial applications showed that compared with the singular value decomposition,this approach is effective to extract not only the weak impacts with the greater kurtosis in time waveform,but also the fault feature frequencies in frequency spectrum.
feature extraction;continuous wavelet transformation;nonlinear manifold learning;impact fault
TH165.3
A
国家自然科学基金项目(51075323,50705073);中央高校基本科研业务费专项资金资助(xjj20100066);北京交通大学轨道车辆结构可靠性与运用检测技术教育部工程研究中心开放课题(SROM RGV(BJTU)2010-002)
2010-06-17 修改稿收到日期:2010-12-13
栗茂林 女,博士生,讲师,1978年12月生

