一种具有双控制比例因子的最优间隔超球分类器
张培林,吴定海,王怀光,王正军,王国德
(军械工程学院,石家庄 050003)
一种具有双控制比例因子的最优间隔超球分类器
张培林,吴定海,王怀光,王正军,王国德
(军械工程学院,石家庄 050003)
针对支持向量描述只考虑目标类训练样本,结合支持向量机最优分类超平面和支持向量描述的思想,引入了异常样本信息的监督机制,建立了最优间隔超球分类器模型,以一个最小的超球包含目标类训练样本和一个尽可能大的超球体将非目标样本隔离在超球体外,使决策超球面与该两个超球面以最大间隔分离,保证了描述精度和泛化性能,同时,为更好地排除对两类样本数据分布中野点的干扰,提出了一种双控制比例因子的控制方法,更加灵活地实现软间隔分类,仿真实例验证了该分类器具有比SVDD更好的分类性能。
模式识别;统计学习;最优分类超球面;控制比例因子
Vapnik[1]提出了的支持向量机,是建立在统计学习理论的基础上,通过引入了核函数映射、松弛变量、凸二次优化等[2]技术,使得支持向量机在遵循结构风险最小化的原则下获得了最好的泛化性能,被广泛应用于数据处理、模式识别等领域[3-4]。
关于样本数据分布不平衡的机器学习问题,Tax[5]等在支持向量机的基础上提出了支持向量描述(Support Vector Data Description,SVDD),只需要目标类数据训练样本,在高维核映射空间建立一个最小的超球将目标数据包括在球内,而非目标数据尽量排除在球外,从而实现正确的分类。但是,这是一种无监督的学习方法,没有利用异常数据样本的分布信息,模型参数一般难以确定,在注重模型的描述精度的同时却丧失了泛化性能。
针对以上问题,本文结合了支持向量机最优分类超平面和支持向量描述的超球体数据描述的思想,提出了一种具有双控制比例因子的最优间隔超球体分类器,在映射的高维特征空间中寻求一个决策超球体将两类数据样本以最大间隔分离,同时,双控制比例因子可以实现更灵活的两类样本分类边界的控制,排除野点的干扰,仿真实例验证了本文模型相对于SVDD的优越性。
1 支持向量机的最优分类面
1.1 最优分类超平面
支持向量机通过核函数将输入空间映射到一个高维的特征空间,然后在特征空间中通过最大化分类间隔来构造最优分类超平面。
构建的最优分类超平面如图1所示,H为分类超平面,H1、H2分别为通过各类样本中离超平面最近点且平行于分类超平面的超平面,H1,H2之间的距离为两类样本的最大分类间隔,即为所谓的最优分类超平面就是要求分类超平面不但能够将两类无错误分开,而且要使其分类间隔最大,即保证了经验风险最小,而且使得支持向量机在遵循结构风险最小化的原则下获得了最好的泛化性能。
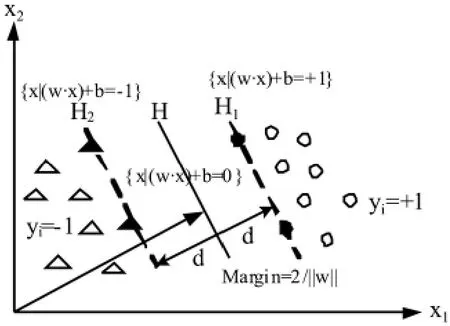
图1 最优分类超平面示意图Fig.1 Optimal separation hyper-plane
1.2 最优分类超球面
如图2所示,设yi∈{-1,1}为相应的类标,借鉴以上支持向量分类超平面的思想,将数据样本映射到高维核特征空间,寻求这样一个同心超球体,其中H(a,R)为决策超球面,H+(a,R+)和 H-(a,R-)为与决策超球面同球心的超球面,同时,最小化H+(a,R+)将目标类数据样本包含在其中,最大化H-(a,R-)将非目标数据样本排除在超球体外,在实现正确的分类的同时使该两分界面能够将两类样本以最大间隔分离,从而确定与该两个分类面具有最优间隔的决策面H(a,R),使该超球分类器模型能够同时兼顾了描述精度和泛化性能。
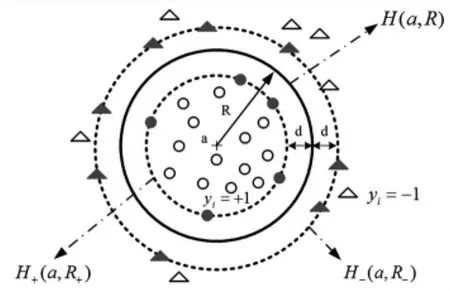
图2 最优分类超球面Fig.2 Hypey-sphere classification with max separation
引入距离变量d,在核空间中寻求一个超球S(a,R),对于两类训练样本有如下约束:

2 最优间隔超球支持向量机
2.1 双控制比例因子
控制比例因子v用于实现软间隔分类,其意义在于:对于检测的数据样本在空间的分布往往存在野点,超球分类器数据描述为了将所有样本包含在超球体内,必然要增大超球半径,导致描述精度的下降。引入控制错分的比例参数使得超球分界面能够提供一种具有弹性的软间隔,将偏离某一类别的奇异点排除在超球外,作为支持向量进行描述,从而缩小超球体积,提高描述的精度。控制比例因子v代替了传统的惩罚参数,具有具体的物理含义,即为边界支持向量比例的上界和支持向量比例的下界,更有利于参数的取值。
对超球支持向量描述模型引入双控制比例因子v1、v2,使v1用于控制目标类样本的边界支持向量,调节软间隔分界面 H+(a,R+),v2用于控制非目标类样本的边界支持向量,调节软间隔分界面 H-(a,R-),实现更加灵活的分类面控制,采用双-v控制技术则可以更灵活地控制两类分类错误,可以有效降低漏检率和虚警概率。
2.2 模型的建立
假设有训练样本个数n,其中目标类训练样本的个数为m1,非目标类训练样本个数为m2,所求决策超球体半径为R,模型可描述为:

对该模型的解释:第一项是在权衡目标数据类样本和非目标数据类样本分布后,求取最为紧凑的决策超球面;第二项解释为最大化两类数据的分类间隔(如图2所示,以2d的间隔分离);第三项引入目标类松弛变量因子ξi和控制比例因子v1,以软间隔来描述正域边界H+(a,R+),第四项为引入非目标类松弛变量因子 ξj和控制比例因子 v2控制的负域软间隔边界 H-(a,R-)。
为求解上述最优化问题,构造Lagrange函数

对以上的 Lagrange 函数,分别对变量 R,d,a,ξi,ξj求偏导求极值
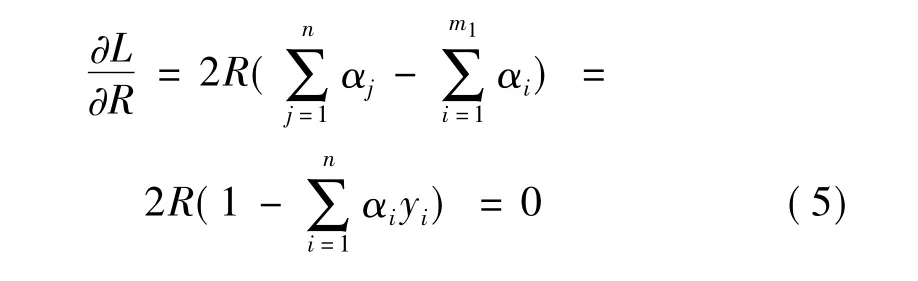

通过解最优化问题,可知超球的球心为:

该模型的正域决策超球面H+(a,R+):

负域的决策超球面H-(a,R-):

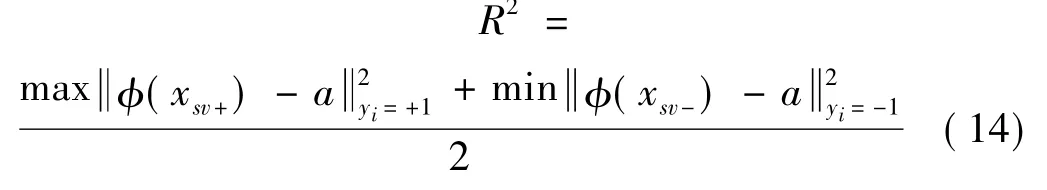
求解完成后,模型的判别函数为:
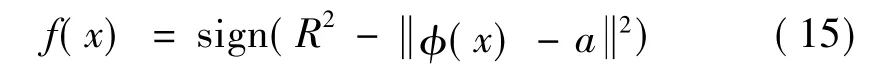
2.3 模型支持向量分析
支持向量的确定至关重要,在该模型中,由拉格朗
类似SVM,最优分类决策超球面:日乘子αi可知隶属于正域H+(a,R+)和负域 H-(a,R-)支持向量的集合为:

经过超球支持向量训练后,各数据样本点及支持向量应分布如下:

3 Banana数据集仿真分析
3.1 松弛因子仿真分析
为分析模型控制比例因子对超球分类面的影响,以prtool[6]工具箱产生的Banana数据集作为测试数据集,两类样本间具有较好的可分性,产生测试样本200个,其中含目标类数据样本160个,非目标类测试样本40个,设置模型的核参数σ=5,不同的控制比例因子下分类面如图3所示。
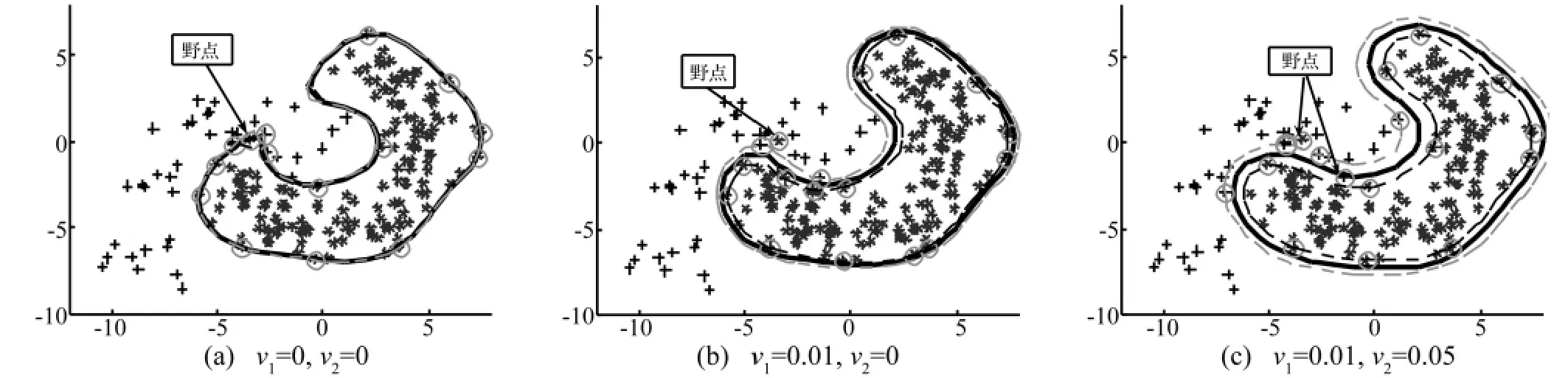
图3 不同控制比例因子下的超球分界面Fig.3 Hyper-sphere of different proportion control parameters
该仿真实例主要用于考查控制比例因子对于消除野点干扰的作用,如图3(a)中所示,当控制比例因子均取0时,由于其中一目标类样本点偏离较远,在这里将其视为野点,三个分界面几乎重叠在一起,体现不出两类样本间的可分性,图3(b)中,设置目标类控制比例因子为0.01,则将该野点排除在正域分界面之外,以支持向量来描述,图3(c)中设置非目标类控制比例因子为0.05,将偏离非目标类样本较远的野点排除在负域之外,以支持向量来描述。
不同控制比例因子下,超球体分界面半径的变化如表1所示,由表中也可以看出,通过控制比例因子的调整排除野点干扰后,超球半径发生了较为明显的变化,同时正负域之间的可分性更加明显,描述精度提高,泛化性能增强。

表1 不同控制比例因子下各超球分界面半径Tab.1 Hyper-sphere radius of different control parameters
3.2 分类器性能对比分析
对于解决不平衡数据分类问题来说,使用准确率作为分类器性能的评价标准是不合适的。评价此类模型性能的好坏最为有效的是ROC(Receiver operating characteristics,ROC)[6]曲线。ROC 曲线从以下两个方面来全面刻画分类器的性能,横坐标为对正常样本正确判别率,纵坐标为异常样本被识别为正常的概率,并采用ROC曲线下面积(Area Under Curve,AUC)代替ROC曲线对分类器的性能进行定量评价,显然AUC∈[0,1],且AUC越大,分类精度越高,整体的泛化性能越好。
下面就以UCI标准的测试数据集[7]对该分类器进行测试,对标准数据集的设置如表2所示,取部分的数据进行训练,其余部分进行测试,对于多类的数据集,只取其中某一类作为目标数据。从训练样本可以看出,训练时,目标数据与非目标数据明显差异较大,体现了数据样本分布不平衡。
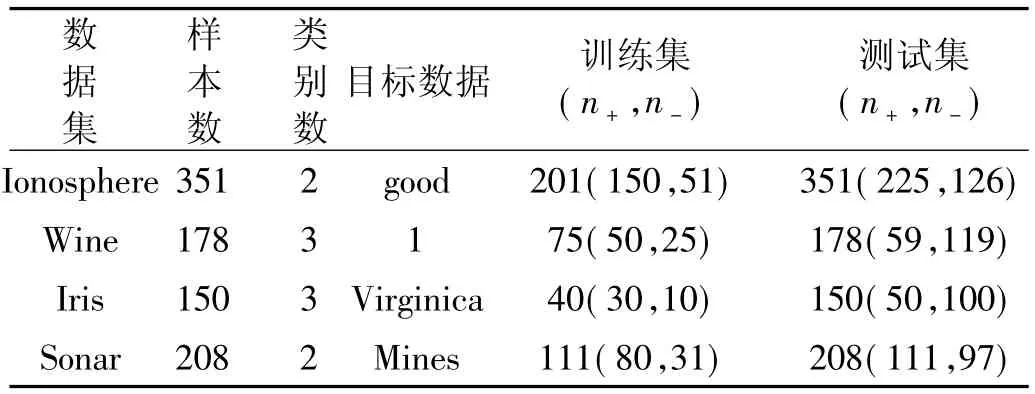
表2 UCI标准测试数据集Tab.2 UCI standard test data sets
利用粒子群优化算法分别对模型参数进行优化,优化后的模型参数及测试结果的对比分析如表3所示,可以看出,在相同的训练、测试条件和最优参数下,本文提出的分类器对任意一个测试数据集的分类性能明显要优于SVDD,在针对数据样本分布不平衡问题时,本文提出的引入异常类样本信息的监督作用和双控制比例因子对于提高超球分类器性能具有重要影响,能够有效提高分类器的泛化性能。

表3 测试结果对比分析Tab.3 Contrastive analysis of test results
4 结论
对于解决模式识别中数据样本分布不平衡问题,本文在深入分析支持向量描述模型的基础上,借鉴支持向量机最优分类超平面的思想,建立了最优间隔超球分类器模型,分析了该模型的支持向量分布,并通过仿真实例来验证该模型的分类性能,得出以下结论:
(1)该模型通过引入了异常样本信息的监督机制,在核特征空间中将两类样本以最大间隔分离,在提高分类器描述精度的同时增强了泛化性能;
(2)引入的双控制比例因子使得该模型可以更加灵活地控制两类分界面的软间隔边界,更好地排除野点的干扰,进一步提高分类器性能。
[1] Vapnik V.The nature of statistical learning theory[M].New York:Springer- Verlag,1995.
[2]Vladimir N V.Statistical learning theory[M].许建华,张学工,译.1版.北京:电子工业出版社,2004:324-360.
[3]张 曦,阎威武,刘振亚,等.基于核主元分析和邻近支持向量机的汽轮机凝汽器过程监控和故障诊断[J].中国电机工程学报,2007,27(14):56-60.
[4]皋 军,王士同.基于矩阵模式的最小类内散度支持向量机[J].电子学报,2009,37(5):1051-1057.
[5] Tax D,Duin R.Support vector domain description[J].Pattern Recognition Letters,1999,20:1191 -1199.
[6] Tax D M J,Duin R P W.Support vector data description[J].Machine Learning Research,2004,(54):45 -66.
[7] Blake C L,Merz C J.UCI repository of machine learning database[EB/OL].http://www.ics.uci.edu/~ mlearn/MLrepository.html.
An optimal separation hyper-sphere classification model with double proportion control parameters
ZHANG Pei-lin,WU Ding-hai,WANG Huai-guang,WANG Zheng-jun,WANG Guo-de
(Ordnance Engineering College,Shijiazhuang 050003,China)
After analyzing the disadvantage of unsupervised training of support vector data description(SVDD),combining the advantage of optimal separation hyper-plane and SVDD,and inducing the supervision of information of negative class,a hyper-sphere classification model with optimal separation was proposed.With one minimum hyper-sphere containing positive class and one hyper-sphere as big as possible excluding negative class,the decision hyper-sphere was made to separate itself and the two hyper-spheres with the max distance to improve the model's description accuracy and generalization performance.To remove the interference of bad points,a method with double proportion control parameter was proposed,it could realize soft separation.Simulation results of Banana and UCI data sets showed that the proposed model has better classification performance than SVDD.
pattern recognition;statistical learning;optimal separation hyper sphere;proportion control parameter
TH17;TP391.4
A
2010-08-16 修改稿收到日期:2010-11-25
张培林 男,教授,博士生导师,1955年生

